Decomposing the response of the stratospheric Brewer–Dobson circulation to an abrupt quadrupling in CO₂

We perform time-slice experiments using HadGEM3-A to decompose the long-term (years 101–150) response of the Brewer–Dobson circulation (BDC) to an abrupt quadrupling in CO₂ (4×CO₂) into (1) a rapid atmospheric adjustment, (2) a contribution from the global-average sea surface temperature (SST) change (+3.4 K), and (3) an SST pattern effect. The SST fields are derived from the CMIP5 multi-model ensemble. Two further experiments explore the impact on the BDC of the spread in global-average SST response to 4×CO₂ across the CMIP5 models (range 2.1–4.9 K). At 70 hPa (10 hPa) the annual-mean tropical upward mass flux increases by 45 % (35 %) due to the 4×CO₂ perturbation. At 70 hPa, around 70 % of the increase is from the global-uniform SST warming, with the remainder coming in similar contributions from the rapid adjustment and SST pattern effect. In contrast, at 10 hPa the increase in mass flux comes mainly from the rapid adjustment (∼40 %) and the uniform SST warming (∼45 %), with a small contribution from the SST pattern. At 10 hPa, the effect of the multi-model spread in global-mean SST is comparable in magnitude to the rapid adjustment. Conversely, at 70 hPa the effect of spread in global-mean SST is substantially larger than both the rapid adjustment and the SST pattern effect. We derive an approximately linear sensitivity of the tropical upward mass flux to global surface air temperature change of 0.62×10⁹ kg s⁻¹ K⁻¹ (9 % K⁻¹) at 70 hPa and 0.10×10⁹ kg s⁻¹ K⁻¹ (6 % K⁻¹) at 10 hPa. The results confirm the most important factor for the acceleration of the BDC in the lower stratosphere under increased CO₂ is global SST changes. We also quantify for the first time that the rapid adjustment to CO₂ is of similar importance to SSTs for the increased BDC in the upper stratosphere. This demonstrates a potential for a fast and slow timescale of the response of the BDC to greenhouse gas forcing, with the relative prominence of those timescales being height dependent.

1 Introduction

The residual circulation in the stratosphere, or the Brewer–Dobson circulation (BDC), is characterized by slow ascent in the tropics, poleward flow, and downwelling in the subtropics and extratropics (Andrews et al., 1987; Holton et al., 1995; Plumb, 2002). There is a strong seasonality in the strength and width of the BDC (Rosenlof, 1995). In the winter hemisphere, the poleward mass transport that occurs in the middle and upper stratosphere is termed the deep branch, while the shallow branch in the lower stratosphere is present year-round in both hemispheres (Birner and Bönisch, 2011). The BDC controls the transport and distribution of radiatively active trace gases such as stratospheric ozone and water vapour (Brewer, 1949; Dobson, 1956), as well as the lifetimes of chemically important trace gases such as chlorofluorocarbons (CFCs; Butchart and Scaife, 2001). The BDC is a wave-driven circulation forced by breaking of planetary-scale Rossby waves and small-scale gravity waves (Holton et al., 1995). The torque imposed by the wave breaking allows flow across lines of constant angular momentum.

General circulation models (GCMs) and chemistry–climate models (CCMs) consistently simulate an acceleration of the BDC in scenarios that include increasing greenhouse gas concentrations (Rind et al., 1990, 2002; Sigmond et al., 2004; Butchart et al., 2006, 2010; Fomichev et al., 2007; Olsen et al., 2007; Deckert and Dameris, 2008; Garcia and Randel, 2008; Li et al., 2008; Calvo and Garcia, 2009; McLandress and Shepherd, 2009; Oman et al., 2009; SPARC, 2010; Garny et al., 2011; Shepherd and McLandress, 2011; Lin and Fu, 2013; Hardiman et al., 2014). A strengthened BDC increases stratosphere–troposphere exchange (STE) of ozone (Rind et al., 2002; Hegglin and Shepherd, 2009; Banerjee et al., 2016) and affects projected ozone trends in the tropical lower stratosphere (e.g. Keeble et al., 2017), subtropics (e.g. Li et al., 2009), and polar regions (e.g. Oman et al., 2009).

The wave forcing that drives the BDC arises from various types of waves generated in the troposphere with different temporal and spatial scales (e.g. Randel et al., 2008), which propagate upwards, break, and dissipate their momentum and energy (Holton et al., 1995; Plumb and Eluszkiewicz, 1999; Semeniuk and Shepherd, 2001). Changes in the BDC must, therefore, be accompanied by changes in stratospheric wave forcing. Three main mechanisms for the altered wave forcing of the BDC under climate change have been considered in the literature: (1) changes in the strength of tropospheric wave generation; (2) changes in the latitudinal distribution of wave forcing within the stratosphere in the vicinity of the turnaround latitudes, which separate the areas of tropical upwelling from extratropical downwelling; and (3) changes in the vertical penetration of tropospheric wave forcing into the stratosphere. Anomalous wave activity emanating from the extratropical troposphere has been shown to have a minimal impact on the overall strength of the BDC because it generally does not induce a torque in the vicinity of the turnaround latitudes (Butchart and Scaife, 2001; Sigmond et al., 2004; Garcia and Randel, 2008; Garny et al., 2011).

Many studies have pointed to an important role for the projected strengthening and upward shift of the subtropical jets with tropospheric warming to explain modelled increases in the BDC under climate change. Rossby wave breaking regions such as the upper flanks of the subtropical jets generally follow critical layers as demonstrated by the observational study of Randel and Held (1991). The robust change in the pattern of zonal winds under climate change (Collins et al., 2013) moves the Rossby wave critical layers in the lower stratosphere upward, enabling enhanced penetration of Rossby wave activity in the subtropical lower stratosphere and an altered distribution of momentum deposition (Rind et al., 1990; Garcia and Randel, 2008; McLandress and Shepherd, 2009; Calvo and Garcia, 2009; Garny et al., 2011). Consistent with this theoretical basis, the multi-model spread in the end of 21st century lower-stratospheric zonal wind trends near the turnaround latitudes was found to explain ∼70 % of the spread in tropical upward mass flux trends in the lower stratosphere across a set of CCMs (Lin and Fu, 2013). Some studies have also found a role for enhanced excitation of tropical waves under climate change for a strengthened BDC (Deckert and Dameris, 2008; Calvo and Garcia, 2009), but the potential for this to drive an increase in the total mass circulation rather than simply a redistribution within the tropics has been questioned (Garny et al., 2011; Shepherd and McLandress, 2011).

Although the signal of an increased BDC in a warmer climate is a highly robust feature of GCMs and CCMs, there are differences amongst models in the relative contributions to the increase from resolved and parameterized wave forcing (Butchart et al., 2006, 2010; Garcia and Randel, 2008; Calvo and Garcia, 2009; McLandress and Shepherd, 2009; Garny et al., 2011). This may be related to models having different climatological resolved and parameterized wave forcing (e.g. Chrysanthou et al., 2019) and/or the potential for a compensation effect between the different types of wave forcing in driving a change in the BDC (e.g. Cohen et al., 2013; Sigmond and Shepherd, 2014).

To understand the relative importance of different drivers, some modelling studies have performed idealized experiments to decompose the BDC response to climate change into different components. Sigmond et al. (2004) performed experiments with the Canadian Middle Atmosphere Model (CMAM) in which CO₂ was doubled separately in the troposphere and stratosphere. In each case, sea surface temperature (SST) changes were imposed as a fraction of the total SST response according to their respective radiative forcings. Sigmond et al. (2004) showed that the increase in residual circulation in December, January, and February (DJF) caused a small warming in the Arctic lower stratosphere, of which about two-thirds could be attributed to the tropospheric CO₂ doubling and about one-third to the middle-atmospheric CO₂ doubling. Their results were qualitatively consistent with the seminal results of Rind et al. (1990), who performed comparable experiments with the NASA Goddard Institute for Space Studies (GISS) model but over a shorter period.

Olsen et al. (2007) performed experiments for the period 1949 to 1998 with the NASA Goddard Earth Observing System version 4 (GEOS-4) GCM using prescribed observed SSTs. They attributed the increase in residual circulation between the first and last decades of their simulations to a stronger SST gradient between the tropics and middle latitudes, resulting in a greater meridional temperature gradient in the subtropical troposphere and more poleward refraction of planetary-scale Rossby waves in the lower stratosphere. Further simulations by Olsen et al. (2007) added the radiative effects of atmospheric greenhouse gas (GHG) changes and showed a small but insignificant increase in STE trend compared to the SST-only experiments. Oman et al. (2009) performed sensitivity experiments with the GEOS-CCM (based on GEOS-4) to decompose the relative effects of SSTs, GHGs, and halogens on the stratospheric age of air distribution between 1960 and 2100. To isolate the effects of SST changes, they compared simulations using SSTs from two different climate models that differed in their climatological SST. They describe the SST experiment as “tropical SSTs” though the SST changes appear to be imposed globally. This comparison further combines the effects of differences in both global-mean SST and SST patterns between the two climate model datasets, though this was not explicitly discussed. As with all other similar studies, they concluded that increased SSTs contribute to an increase in tropical lower-stratospheric upwelling and a decrease in age of air.

While studies have demonstrated that higher SSTs increase the strength of the BDC (Olsen et al., 2007; Oman et al., 2009; Lin et al., 2015), one confounding factor is that the SST response to anthropogenic forcing shows an inhomogeneous pattern (e.g. Latif and Keenlyside, 2009), which may affect the overall BDC response. For example, regional SST anomalies associated with the El Niño–Southern Oscillation (ENSO) have been shown to affect the BDC both through modulation of the Northern Hemisphere (NH) winter stratospheric circulation (Manzini et al., 2006) and tropical lower-stratospheric upwelling (Marsh and Garcia, 2007; Randel et al., 2009). Using CMAM, Simpson et al. (2011) attribute the increase in boreal winter tropical lower-stratospheric upwelling under El Niño to increased resolved wave forcing in the Southern Hemisphere (SH) subtropical lower stratosphere, which was caused by altered wave sources in the troposphere under El Niño. In contrast, Calvo et al. (2010) using the Whole Atmosphere Community Climate Model (WACCM), attribute the increased tropical upwelling during El Niño to changes in the propagation and dissipation of parameterized gravity waves caused by the anomalous location and intensity of the subtropical jets. Garfinkel et al. (2013) showed that decadal trends comprised of warming in the Indian Ocean and the warm pool region can drive changes in tropical lower-stratospheric upwelling. Therefore, while a uniform SST increase can generate much of the canonical pattern of long-term tropical upper-tropospheric warming, through impacts on tropical convection and the water vapour and lapse rate feedbacks (e.g. Chen et al., 2013), the spatial pattern of SST trends may also affect the BDC. Lin et al. (2015) showed an approximately linear relationship between tropical annual-mean surface temperature and anomalous lower-stratospheric mass flux in the GFDL-CM3 model that held on interannual, decadal, and centennial timescales. However, on multi-decadal timescales this calculation aliases the direct atmospheric radiative effects of GHGs, the SST pattern effect, and the SST magnitude into one term (Olsen et al., 2007; Sigmond et al., 2004)

While previous literature suggests that the distinct radiative effects of GHGs, the SST magnitude, and the SST pattern may contribute to projected changes in the BDC, no previous study has explicitly quantified their importance; this is the goal of our study. Here, we perform climate model experiments to decompose the response of the BDC to an abrupt quadrupling of CO₂ into three components: (1) the rapid adjustment, or direct component, associated with CO₂ radiative effects in the absence of SST change; (2) a contribution from the global-average sea surface temperature (SST) change termed a global uniform SST warming throughout the rest of the study; and (3) the SST pattern effect. The goal is to understand the distinct contributions of the three components and assess the extent to which they can be combined to explain the overall BDC response. We further compare the magnitudes of the rapid adjustment and SST pattern effects on the BDC with the effect of spread in global-mean SST change due to CO₂ across climate models. The remainder of the paper is laid out as follows: Sect. 2 describes the atmospheric model and experimental set-up; Sect. 3 presents the results, and Sect. 4 summarizes our main findings and conclusions.

2 Data and methods

2.1 Atmospheric model description

We use the Hadley Centre Global Environment Model version 3 (HadGEM3) variant of the Met Office Unified Model (MetUM) version 8.4, which has been used for both numerical weather prediction and climate simulation. It is configured with the Global Atmosphere (GA4.0) and comprises a non-hydrostatic fully compressible dynamical core that uses a semi-implicit semi-Lagrangian advection scheme in terrain-following hybrid height coordinates (Walters et al., 2014). We run the atmosphere-only configuration (HadGEM3-A) at N96 horizontal resolution (1.875^∘ × 1.25^∘, ∼135 km in mid-latitudes) with 85 levels (L85) from the surface to an altitude of ∼85 km. Interactions of the flow-blocking drag associated with the orographic gravity wave drag (OGWD) are parameterized, as detailed in Webster et al. (2003). Similarly, a spectral sub-grid parameterization is used for the representation of the gravity wave drag induced in the upper stratosphere and mesosphere, forced by non-orographic gravity wave drag (NOGWD) such as convective processes and fronts, which enables HadGEM3 to simulate a realistic quasi-biennial oscillation (QBO) as detailed in Scaife et al. (2002).

2.2 Experiment design

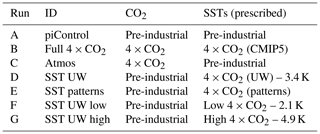
Seven 50-year-long time-slice simulations were performed with HadGEM3-A with fixed boundary conditions including prescribed SSTs and sea ice. The experiment names and IDs are shown in Table 1. The reference simulation (run A) uses boundary conditions, including greenhouse gas (GHG) concentrations and natural and anthropogenic primary aerosol or reactive gas emissions, set to pre-industrial (year 1850) values following the Coupled Model Intercomparison Project 5 protocol (CMIP5; Lamarque et al., 2010; Taylor et al., 2012). The reference SSTs and sea ice concentrations (SICs) are annually repeating fields taken as the monthly-mean multi-model mean (MMM) from the CMIP5 piControl simulations (Taylor et al., 2012). The MMM reference SST and SIC fields are constructed from the average of the last 150 years of the piControl experiments from the 26 CMIP5 models listed in the Supplement (Table S1).

Figure 1 Prescribed annual-mean SST anomalies (K) with respect to the piControl climatology in the (a) full 4×CO₂, (b) uniform SST warming, and (c) SST pattern perturbation experiments.

Table 1 The sensitivity experiments used in this study with the atmospheric CO₂ and the SSTs used as boundary conditions. All other boundary conditions are as in piControl.

Six perturbation experiments are performed to isolate different components of the long-term response in the CMIP5 abrupt 4×CO₂ experiment, which instantaneously quadruples CO₂ from its pre-industrial concentration. We first calculate the CMIP5 monthly-mean MMM SST in the abrupt 4×CO₂ experiment using the final 50 years (years 101–150) of each model run (Table S1). The annual-mean SST anomalies compared to the reference pre-industrial state are shown in Fig. 1a. Note that in all the perturbation experiments, SIC is held fixed at the reference values. This is artificial, but it enables the effects of SSTs on the BDC and associated mechanisms to be isolated from the possible effects of changing sea ice on the stratosphere (e.g. Kim et al., 2014; McKenna et al., 2018). We performed a separate experiment in which SIC was also changed to the CMIP5 MMM 4×CO₂ response along with global SSTs and atmospheric CO₂, but this showed no significant effect of changing SIC on the BDC (not shown) and therefore will not be discussed further.

The first perturbation experiment (run B) accounts for the full (atmosphere + SST) abrupt 4×CO₂ response and is designed to simulate the long-term centennial response to CO₂ forcing. The second perturbation experiment (C) only accounts for the CO₂ rapid adjustment by quadrupling atmospheric CO₂ concentrations while holding SSTs and SIC at their pre-industrial values. The third experiment (D) imposes a monthly-varying globally uniform SST anomaly derived from the global-mean multi-model mean 4×CO₂ SST anomaly relative to the control. In the annual and multi-model mean this is equal to 3.4 K (Fig. 1b). Note the CMIP5 MMM global SST anomaly is smaller than the global-mean surface air temperature (GSAT) change in the abrupt 4×CO₂ experiment because land areas warm more than the ocean (e.g. Joshi and Gregory, 2008). In the fourth perturbation experiment (E), we subtract the monthly-varying uniform warming value from the 4×CO₂ anomalies to impose the local deviations in SST from the global uniform value (i.e. the SST pattern). The SST pattern is shown in Fig. 1c; it is comprised of relatively stronger warming across the tropics in the Pacific, Atlantic, and Indian Ocean basins and in the North Pacific and relatively weaker warming across the Southern Ocean, in the North Pacific warming hole region, and in the vicinity of the South Pacific stratocumulus decks.

By construction, the sum of the SST anomalies in runs D and E equals the full SST anomalies of run B. Note that the change in annual-mean GSAT simulated in runs B and D (4.3 and 4.0 K, respectively) is larger than the imposed global-mean SST anomaly, partly because of the enhanced warming response over land. While SSTs are held fixed in run C, there are changes to land temperatures that cause a small GSAT response (0.43 K). Finally, although the global-mean SST change in run E is zero by construction, there are changes to land temperatures that lead to a small GSAT response (0.45 K).

There is substantial inter-model spread in the modelled global-mean SST change in the abrupt 4×CO₂ experiments (Flato et al., 2013). To investigate the effect of this spread on the BDC, and to place the rapid adjustment and SST pattern effects into the context of model uncertainty in the global surface warming due to CO₂, we perform two further uniform SST warming sensitivity runs. These are chosen to be the lowest (annual-mean ∼2.1 K; run F) and highest (annual-mean ∼4.9 K; run G) global-mean SST changes from the 26 CMIP5 models used in this study. These values come from the INMCM4 (Volodin, 2013) and IPSL-CM5A-LR (Dufresne et al., 2013) models, respectively. The annual-mean GSAT change in runs F and G is 3.0 and 6.1 K, respectively.

Since HadGEM3-A does not include interactive chemistry, we prescribe zonal-mean pre-industrial ozone concentrations in all the experiments following the Coupled Model Intercomparison Project 6 (CMIP6; Eyring et al., 2016) protocol, based on the CMIP6 experiments run with HadGEM3-GC3.1 (Kuhlbrodt et al., 2018; Williams et al., 2018). It should be noted that keeping ozone concentrations fixed in all our experiments will implicitly neglect the effects of any ozone feedbacks from both the chemical effects of increased CO₂ and the transport effects from an altered BDC; this includes effects on the thermal structure of the upper troposphere, especially around the tropical upper troposphere and lower stratosphere (Nowack et al., 2015; Chiodo and Polvani, 2017) and on upper-stratospheric temperatures (Maycock, 2016).

2.3 Residual circulation diagnostics

To diagnose the BDC and its changes, we make use of the transformed Eulerian mean (TEM) circulation diagnostics (Andrews et al., 1987; Andrews and McIntyre, 1976, 1978) as calculated internally by the model. The TEM residual circulation velocities (${\stackrel{\mathrm{‾}}{v}}^{*}$, ${\stackrel{\mathrm{‾}}{w}}^{*}$) are defined as in Andrews et al. (1987):

$$\begin{array}{}\text{(1)}& \begin{array}{rl}& {\stackrel{\mathrm{‾}}{v}}^{*}=\stackrel{\mathrm{‾}}{v}-{\displaystyle \frac{\mathrm{1}}{{\mathit{\rho }}_{\mathrm{0}}}}{\displaystyle \frac{\partial }{\partial z}}\left[{\displaystyle \frac{{\mathit{\rho }}_{\mathrm{0}}\stackrel{\mathrm{‾}}{v^{\prime }{\mathit{\theta }}^{\prime }}}{\partial \stackrel{\mathrm{‾}}{\mathit{\theta }}/\partial z}}\right],\\ & {\stackrel{\mathrm{‾}}{w}}^{*}=\stackrel{\mathrm{‾}}{w}+{\displaystyle \frac{\mathrm{1}}{a\cos \mathit{\phi }}}{\displaystyle \frac{\partial }{\partial \mathit{\phi }}}\left[{\displaystyle \frac{\stackrel{\mathrm{‾}}{v^{\prime }{\mathit{\theta }}^{\prime }}\cos \mathit{\phi }}{\partial \stackrel{\mathrm{‾}}{\mathit{\theta }}/\partial z}}\right],\end{array}\end{array}$$

where overbars denote a zonal-mean quantity and primes the departure from the zonal mean. v and w are the meridional and vertical components of wind velocity, respectively, ρ₀ is the log-pressure density, $z=-H\ln (p/p_{\mathrm{s}})$ is the log-pressure vertical coordinate (height), H is the scale height, p is the pressure at a specified level with p_s the pressure at the surface, $\stackrel{\mathrm{‾}}{v^{\prime }{\mathit{\theta }}^{\prime }}$ is the eddy heat flux, θ is the potential temperature, α is the Earth radius, and ϕ is the latitude. Using ${\stackrel{\mathrm{‾}}{v}}^{*}$ from Eq. (1) we further calculate the residual mass streamfunction ${\stackrel{\mathrm{‾}}{\mathrm{\Psi }}}^{*}(\mathit{\varphi }$, z) as

$$\begin{array}{}\text{(2)}& {\stackrel{\mathrm{‾}}{\mathrm{\Psi }}}^{*}(\mathit{\varphi },z)={\displaystyle \frac{\mathrm{2}\mathit{\pi }\mathit{\alpha }\cos \mathit{\varphi }}{g}}\underset{\mathrm{bottom}}{\overset{\mathrm{top}}{\int }}{\stackrel{\mathrm{‾}}{v}}^{*}\mathrm{d}p,\end{array}$$

where g is the acceleration due to gravity. Equation (2) is integrated from the top of atmosphere to the surface using the boundary condition that ${\stackrel{\mathrm{‾}}{\mathrm{\Psi }}}^{*}=\mathrm{0}$ at the top of the atmosphere (p=0). Subsequently, we calculate the net downward mass flux in each hemisphere, by finding ${\stackrel{\mathrm{‾}}{\mathrm{\Psi }}}_{\max }^{*}$ and ${\stackrel{\mathrm{‾}}{\mathrm{\Psi }}}_{\min }^{*}$ in the NH and SH, respectively, at each pressure level. The net tropical upward mass flux, which is equal to the sum of the downward mass fluxes in each hemisphere, can then be expressed as (Rosenlof, 1995)

$$\begin{array}{}\text{(3)}& \mathrm{tropical}\mathrm{upward}\mathrm{mass}\mathrm{flux}=\mathrm{2}\mathit{\pi }a\left({\stackrel{\mathrm{‾}}{\mathrm{\Psi }}}_{\max }^{*}-{\stackrel{\mathrm{‾}}{\mathrm{\Psi }}}_{\min }^{*}\right).\end{array}$$

We apply the “downward control” principle (DCP; Haynes et al., 1991) to further separate the contributions to the tropical upward mass flux from resolved waves due to the divergence of Eliassen–Palm flux (EPF) and contributions from OGWD and NOGWD. Resolved waves and parameterized gravity wave drag (OGWD/NOGWD) constitute the eddy-induced total zonal forces $\stackrel{\mathrm{‾}}{F}$. Under steady-state conditions, the ${\stackrel{\mathrm{‾}}{\mathrm{\Psi }}}^{*}(\mathit{\varphi }$, z) at a specified log(pressure) height, z, is related to the vertically integrated $\stackrel{\mathrm{‾}}{F}$ above that level along a surface of constant zonal-mean absolute angular momentum $\stackrel{\mathrm{‾}}{m}=a\cos \mathit{\varphi }(\stackrel{\mathrm{‾}}{\mathit{\upsilon }}+a\mathrm{\Omega }\cos \mathit{\varphi })$, where $\stackrel{\mathrm{‾}}{\mathit{\upsilon }}$ is the zonal-mean zonal wind and Ω is Earth's rotation rate (Haynes et al., 1991). Outside of the tropics, $\stackrel{\mathrm{‾}}{m}$ is approximately constant at a fixed latitude, ϕ, resulting in the following equation (Haynes et al., 1991):

$$\begin{array}{}\text{(4)}& {\stackrel{\mathrm{‾}}{\mathrm{\Psi }}}^{*}(\mathit{\varphi },z)=\underset{z}{\overset{\mathrm{\infty }}{\int }}{\left\{{\displaystyle \frac{{\mathit{\rho }}_{\mathrm{0}}{a}^{\mathrm{2}}\stackrel{\mathrm{‾}}{F}{\cos }^{\mathrm{2}}\mathit{\varphi }}{{\stackrel{\mathrm{‾}}{m}}_{\mathit{\varphi }}}}\right\}}_{\mathit{\varphi }=\mathit{\varphi }\left(z^{\prime }\right)}\mathrm{d}z,\end{array}$$

where ${\stackrel{\mathrm{‾}}{m}}_{\mathit{\varphi }}\approx -\mathrm{2}\mathrm{\Omega }{a}^{\mathrm{2}}\sin \mathit{\varphi }\cos \mathit{\varphi }$ is the quasi-geostrophic limit. The boundary conditions are ${\stackrel{\mathrm{‾}}{\mathrm{\Psi }}}^{*}\to \mathrm{0}$ and ${\mathit{\rho }}_{\mathrm{0}}{\stackrel{\mathrm{‾}}{w}}^{*}\to$ as z→∞.

3 Results

3.1 Zonal-mean temperature response

Figure 2 shows latitude–pressure cross sections of the annual-mean and zonal-mean temperature anomalies from the reference pre-industrial simulation for perturbation runs B–E. The full response (Fig. 2a) exhibits the canonical pattern of temperature change due to increased CO₂, with tropospheric warming that maximizes in the tropical upper troposphere (by ∼8 K) and stratospheric cooling that increases with height (Collins et al., 2013). Note that Arctic amplification in the lower troposphere is small here compared to coupled atmosphere–ocean models (Collins et al., 2013), presumably because we do not impose sea ice changes in the runs.

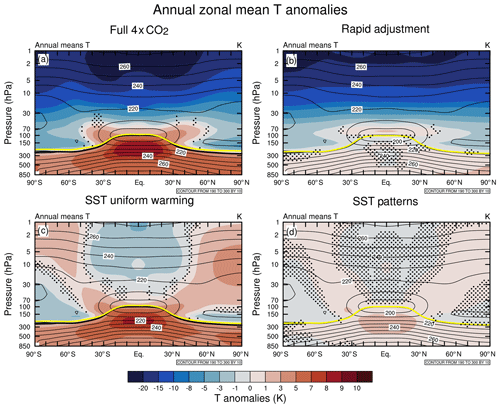
Figure 2 Latitude vs. pressure cross sections of annual-mean and zonal-mean temperature anomalies (K) between 850 and 1 hPa with respect to the piControl simulation for the (a) 4×CO₂ (run B), (b) rapid adjustment (run C), (c) uniform SST warming (run D), and (d) SST pattern (run E) experiments. Contours show the piControl climatology. Stippling denotes where the differences are not statistically significant at the 95 % confidence level using a two-tailed Student's t test. Thick yellow and black lines indicate the tropopause pressure levels in each perturbation run and in the reference simulation, respectively.

The rapid adjustment due to changes in atmospheric CO₂ (Fig. 2b) accounts for most of the stratospheric cooling seen in the full response, with cooling of ∼15 K in the upper stratosphere. However, the stratospheric cooling in run C (Fig. 2b) is more uniform in latitude than in the full experiment and more closely resembles the purely radiative response to CO₂ (Fels et al., 1980). In the troposphere, the rapid adjustment induces a weak (<1 K) warming that is fairly homogeneous and comes partly from the small changes in GSAT, since land temperatures are not held fixed. Most of the tropospheric zonal-mean warming is reproduced by imposing the uniform SST warming (Fig. 2c), including the tropical upper-tropospheric amplification of up to 9 K and the extension of warming into the subtropical lower stratosphere in both hemispheres. In the stratosphere, the uniform SST warming induces an anomalous meridional temperature gradient, with cooling of 2–3 K in the tropical middle and upper stratosphere and warming in the extratropics and polar regions. This pattern accounts for most of the latitudinal variation in stratospheric cooling seen in the full response (Fig. 2a).

The SST pattern experiment (Fig. 2d) exhibits a similar morphology in the temperature response to the uniform SST warming run, albeit much weaker in amplitude. In the troposphere, the SST pattern induces a weak warming that is comparable in magnitude to the rapid adjustment (Fig. 2b), but with a weak upper-tropospheric amplification that enhances the effect of the uniform warming (Fig. 2c). This upper-tropospheric amplification suggests enhanced tropical deep convection, which may be consistent with the imposed anomalous tropical SST warming (Fig. 1c).

The thick yellow lines in Fig. 2 denote the tropopause pressure for each perturbation experiment. These can be compared to the climatological tropopause in the reference simulation (thick black lines). The lifting of the tropopause by ∼1 km within the deep tropics in the full experiment comes mainly from the uniform SST warming (∼80 %) with the remaining 20 % coming from the SST pattern. However, the maximum tropopause lifting (>1.2 km) occurs in the extratropics of both hemispheres, especially over the Arctic polar cap (not shown).

Figure 3 As in Fig. 2, but for the annual and zonal-mean zonal wind anomalies (m s⁻¹) between 850 and 1 hPa. Contours show the piControl climatology. The thick black lines denote the critical lines for stationary waves ($\stackrel{\mathrm{‾}}{u}=\mathrm{0}$) in piControl, and the thick yellow lines denote each perturbation experiment.

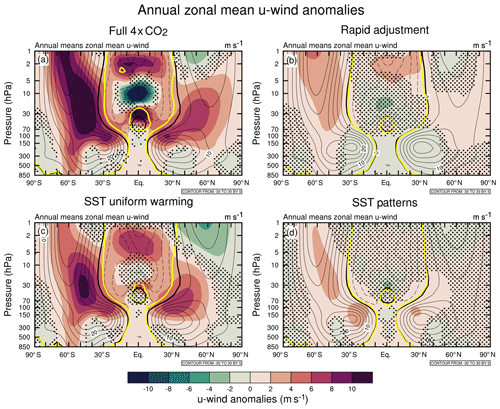
3.2 Zonal-mean zonal wind response

The annual-mean zonal-mean zonal wind anomalies in the four perturbation experiments are shown in Fig. 3. The full 4×CO₂ response (Fig. 3a) shows the familiar pattern of a strengthening and upward shift of the subtropical jets, a strengthening and poleward shift of the mid-latitude westerlies in the SH, and increased westerlies in the SH stratosphere (Collins et al., 2013). The strengthened subtropical jets arise mainly from the uniform SST warming (Fig. 3c) with a small contribution from the SST pattern (Fig. 3d). In contrast, the rapid adjustment (Fig. 3b) does not induce a strengthening of the subtropical jets, but it does explain a significant part of the increased westerlies in the SH extratropics, particularly in the upper stratosphere. The SST pattern effect also contributes to the increased SH stratospheric westerlies, but the uniform SST warming shows the largest increase. In the NH, the full experiment shows stronger westerlies in the lower stratosphere and weakened westerlies near the subtropical stratopause. The anomalous lower-stratospheric westerlies are contributed by the uniform warming in the subtropics and mid-latitudes and the rapid adjustment in the extratropics and polar region. The uniform warming also causes weakened westerlies in the subtropical upper stratosphere, with a smaller effect from the rapid adjustment.

The full 4×CO₂ response shows significant zonal wind anomalies in the tropical stratosphere between 50 and 1 hPa, which is also seen in the uniform SST warming experiment. This is likely related to changes to the QBO properties under climate change, which have been noted in other idealized GCM experiments (e.g. Kawatani et al., 2011), though a detailed investigation of the QBO is beyond the scope of this study.

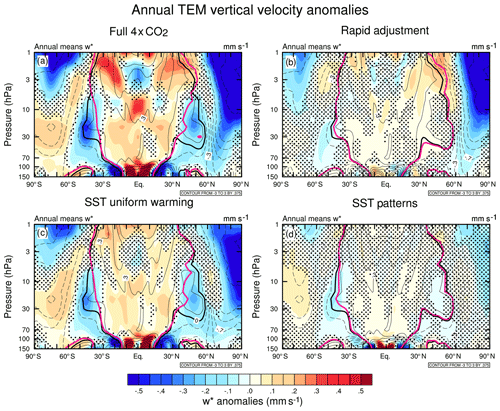
Figure 4 As in Fig. 2, but for the annual-mean TEM residual vertical velocity anomalies (mm s⁻¹) between 150 and 1 hPa. Contours show the piControl climatology and range from −3 to 3 mm s⁻¹ in increments of 0.375 mm s⁻¹. The thick black lines denote the turnaround latitudes (${\stackrel{\mathrm{‾}}{w}}^{*}=\mathrm{0}$) in piControl, and pink thick lines denote each perturbation experiment, respectively.

The zero wind lines ($\stackrel{\mathrm{‾}}{u}=\mathrm{0}$), which demarcate the “critical lines” for linear stationary Rossby waves (Dickinson, 1968), are shown by the thick lines in Fig. 3. In the stratosphere, there is a clear equatorward contraction of the zero wind lines in both hemispheres in the full 4×xCO₂ experiment. Previous studies have connected this to increased penetration of Rossby wave activity into the subtropical lower stratosphere (Shepherd and McLandress, 2011). The contraction of the zero wind lines is primarily due to the uniform SST warming, with a modest contraction also seen in the rapid adjustment and SST pattern experiments.

3.3 Residual circulation response

Figure 4 shows latitude–pressure cross sections of the annual-mean residual vertical velocity (${\stackrel{\mathrm{‾}}{w}}^{*}$) anomalies with respect to the reference simulation for experiments B–E. The uniform SST warming accounts for most of the increased tropical lower-stratospheric upwelling (∼70 % between 30^∘ S and 30^∘N over the layer 100–50 hPa) seen in the full 4×xCO₂ response. However, there are also significant, but small, increases in tropical lower-stratospheric upwelling induced by the rapid adjustment (∼17 %) and the SST pattern perturbations (∼13 %) (Fig. 4b and d). While comparatively small compared to the effect of the uniform SST warming, the increases in ${\stackrel{\mathrm{‾}}{w}}^{*}$ in the tropical lower stratosphere from the SST pattern are broadly comparable in magnitude to the effects of ENSO on tropical upwelling found in other modelling studies (Calvo et al., 2010; Simpson et al., 2011).

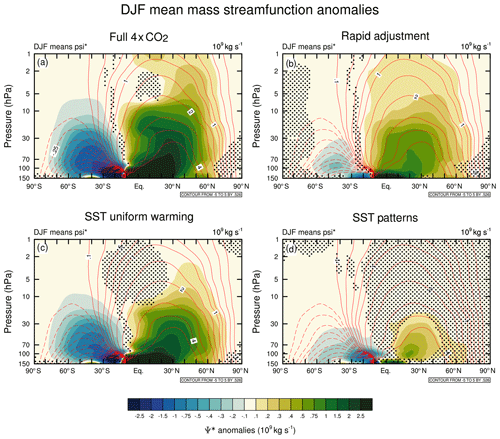
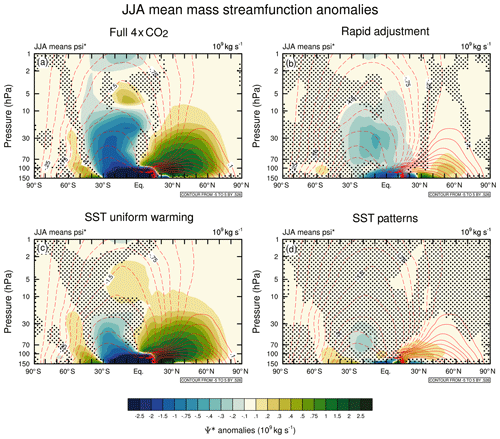
Figure 5 DJF mean residual mass streamfunction anomalies (10⁹ kg s⁻¹) between 150 and 1 hPa with respect to the piControl simulation for the (a) 4×CO₂ (run B), (b) rapid adjustment (run C), (c) uniform SST warming (run D) and (d) SST pattern (run E) experiments. Stippling denotes where the differences are not statistically significant at the 95 % confidence level using a two-tailed Student's t test. Red contours plotted at −5, −4, −3, −2, −1.5, −1, −0.75, −0.5, −0.25, −0.1, 0.1, 0.25, 0.5, 0.75, 1, 1.5, 2, 3, 4, and 5×10⁹ kg s⁻¹ show the piControl climatology with negative values shown in dashed contours.

The turnaround latitudes are overlaid as thick lines in Fig. 4. A quadrupling of CO₂ leads to a narrowing of the upwelling region in the lower and middle stratosphere that maximizes around ∼30 hPa (Hardiman et al., 2014). This arises predominantly from the uniform SST warming (Fig. 4c), with additional weaker contributions from the rapid adjustment and SST patterns (Fig. 4b and d). In contrast, in the upper stratosphere (10 hPa) the upwelling region widens in the NH in particular (see Hardiman et al., 2014). The widening of the upwelling region in the NH upper stratosphere arises almost entirely from the rapid adjustment, while the smaller tropical widening in the SH upper stratosphere is contributed by all three components.

We move now to evaluating the changes in downwelling in the extratropics. The full 4×CO₂ experiment shows enhanced downwelling over the Arctic throughout the stratosphere. Both the rapid adjustment and uniform SST warming induce comparable increases in downwelling in the Arctic, while the SST patterns do not produce significant ${\stackrel{\mathrm{‾}}{w}}^{*}$ changes in this region. In the SH, the full perturbation generates stronger downwelling in the upper stratosphere and weaker downwelling in the middle and lower stratosphere below 10 hPa. All three components produce increased downwelling in the Antarctic upper stratosphere, with the largest change from the uniform SST warming and the rapid adjustment. In the lower stratosphere, the uniform SST and SST patterns both generate reduced downwelling as seen in the full 4×CO₂ experiment.

Figure 6 As in Fig. 5, but for the JJA season.

The relationship of the changes in residual circulation to the overall mass transport in the stratosphere can be seen in Figs. 5 and 6, which show the residual mass streamfunction anomalies (Ψ^*) in the solstice seasons December–February (DJF) and June–August (JJA) in the four experiments. For comparison, the Supplement (Fig. S1) shows the annual-mean Ψ^* responses. As the winter hemisphere cell is the dominant one, the climatological circulation in DJF and JJA is significantly stronger in the NH and SH, respectively. The largest response in both hemispheres occurs in DJF (Fig. 5), while the NH exhibits a stronger response compared to the SH. In DJF, the response to the SST patterns in the NH is confined to the subtropical lower stratosphere (Fig. 5d), while the rapid adjustment (Fig. 5b) and uniform SST warming (Fig. 5c) induce increased poleward transport across most of the stratosphere, with the latter showing around 3 times larger anomalies near the maximum in the subtropical lower stratosphere. The peak NH anomaly due to the rapid adjustment is around double that for the SST patterns in DJF. Specifically, in the lower stratosphere (100–50 hPa) between 0 and 60^∘ N, the uniform SST warming accounts for ∼65 % of the full response, the rapid adjustment contributes ∼26 %, and the SST patterns contribute the remainder. Conversely, in the middle and upper stratosphere between 30 and 1 hPa, over the same latitude bands, the rapid adjustment effect becomes more important, surpassing the contribution of the uniform SST warming accounting for 48 % and 46 % of the full response, respectively. In JJA (Fig. 6), the increase in the SH mass transport is largely is largely present in the subtropics while the opposing changes in the mid-latitude lower stratosphere seen as a reduction in the streamfunction arise from both the uniform SST warming (Fig. 6c) and the SST patterns (Fig. 6d). In the SH subtropical (0–30^∘ S) lower stratosphere (100–50 hPa), the uniform SST warming accounts for ∼70 % of the full response with the rapid adjustment contributing roughly 20 % and the remaining 10 % due to the SST pattern. The strengthened SH poleward transport due to the uniform SST warming is confined to the SH subtropical lower stratosphere, while the rapid adjustment (Fig. 6b) induces poleward flow that also extends into the NH and is associated with the deep branch of the BDC. However, it should be noted that the SH response is generally weaker than in the NH, especially in the middle and upper stratosphere over both solstice seasons. The deep branch of the circulation exhibits distinct hemispheric asymmetries, explaining the differences in the magnitude of downwelling over the SH and NH polar caps seen in Fig. 4. This asymmetry is associated with a significantly stronger poleward NH branch of the circulation compared to its SH counterpart with important contributions by an equally stronger NH mesospheric cell overall (not shown).

We lastly consider the extent to which the combined residual circulation anomalies from the rapid adjustment, global uniform SST, and SST pattern experiments match the full 4×CO₂ response. This comparison is shown in Fig. S2. The main differences are that the combined responses overpredict the enhanced poleward flow in the NH extratropical lower stratosphere, while there are dipole anomalies straddling the Equator in the tropical mid-stratosphere associated with the differences seen in the QBO features across the experiments. Nevertheless, the differences between the linear sum of responses and the full experiment are generally small compared to the overall changes, which supports the use of the experiments to decompose the total response into separate parts.

3.4 Wave forcing and downward control

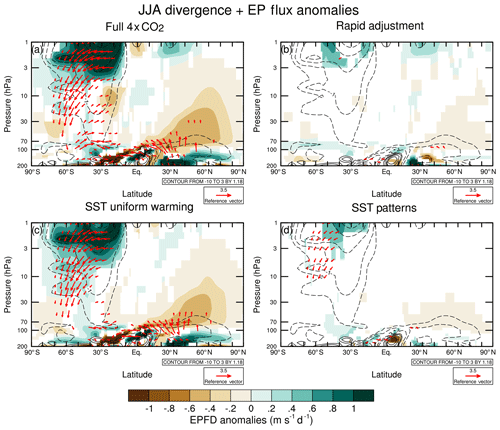
To understand the changes in residual circulation shown in Figs. 4–6, we now focus on the wave forcing in each experiment. As the distribution of wave forcing shows a strong annual cycle, we separate the changes into the winter and summer seasons in each hemisphere (DJF and JJA) as in Figs. 5 and 6. Figure 7 shows the DJF average Eliassen–Palm flux divergence (EPFD) anomalies from the pre-industrial era for runs B–E along with the anomalous EPF vectors. We multiply the EPFD anomalies with cos φ to represent the torque exerted on the zonal flow. The full experiment (Fig. 7a) shows increased EPF divergence in the NH extratropical upper stratosphere and in the mid-latitude middle stratosphere. In the SH, there is a broad region of enhanced EPF convergence peaking around 50–60^∘ S over a layer spanning 3 to 70 hPa. There is a reduction in EPF convergence near the SH subtropical stratopause. Between ∼50^∘ and 70 hPa, there is enhanced EPF convergence in the tropics and subtropics in both hemispheres. This modulation in the location of the maximum in the resolved wave forcing is associated with the equatorward movement of the critical layers (Fig. 3), allowing more Rossby wave activity to penetrate into the subtropical latitudes, accelerating the shallow branch of the BDC, consistent with the findings of Shepherd and McLandress (2011).

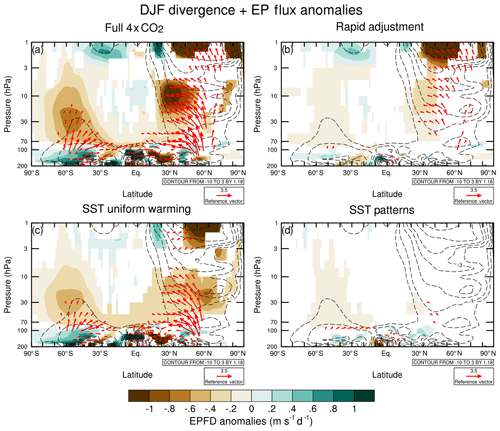
Figure 7 DJF average EPF vector anomalies (red arrows) (m² s⁻²) and EPF divergence anomalies (m s⁻¹ d⁻¹) (shading) between 200 and 1 hPa with respect to the piControl simulation for the (a) 4×CO₂ (run B), (b) rapid adjustment (run C), (c) uniform SST warming (run D), and (d) SST pattern (run E) experiments. The EPF divergence here is multiplied by the cosine of latitude to represent the torque exerted on the zonal flow. Contours show the piControl climatology with contours plotted at −10, −8, −6, −4, −3, −2, −1, −0.5, 0.5, 1, 2, and 3 m s⁻¹ d⁻¹. The EPF vector and divergence anomalies are only plotted where they are significant at the 95 % confidence level using a two-tailed Student's t test. The EPF vectors have been scaled following Edmon et al. (1980) and were scaled by a magnification factor of 5 in the stratosphere in order to enhance their visibility.

The rapid adjustment and uniform SST warming contribute similar increases in EPF convergence in the NH upper stratosphere in DJF (Fig. 7b and c). In the NH middle stratosphere, the uniform SST warming explains most of the increase in EPF convergence seen in the full experiment, but the rapid adjustment does contribute in the region 20–40^∘ N. The uniform SST warming also contributes to most of the increase in EPF convergence in the lower to middle SH extratropical stratosphere in austral summer, but the rapid adjustment and SST pattern (Fig. 7d) do make smaller but significant contributions to the increased wave forcing in that region. The uniform SST warming produces most of the enhanced EPF convergence in the tropical and subtropical upper troposphere–lower stratosphere (UTLS).

Figure 8 shows the EPFD anomalies in JJA in each experiment. The picture in the summer NH in the full experiment is similar to that in the SH in DJF (Fig. 7a). Specifically, there is anomalous EPF divergence in the extratropical lower stratosphere and anomalous EPF convergence in the middle to upper stratosphere, representing an upward shift and extension of the region of climatological EPF convergence in this region (contours). Near the subtropical stratopause there is anomalous EPF divergence that comes mainly from the rapid adjustment (Fig. 8b). The anomalous EPF convergence in the middle stratosphere comes mainly from the uniform SST warming (Fig. 8c) with smaller but significant contributions from the rapid adjustment and SST patterns (Fig. 8d). The winter SH is rather different from the NH in DJF. The full experiment shows anomalous EPF divergence in the SH upper stratosphere, which represents a weakening of the climatological EPF convergence in this region (contours). This is attributed mainly to the uniform SST warming, but there are also significant EPF convergence anomalies near the SH subtropical stratopause from both the rapid adjustment and the SST patterns. The changes in EPFD in the SH middle and lower stratosphere in austral winter have a more complex structure. The full experiment shows a tripolar pattern between 30 and 70 hPa, with anomalous EPF convergence poleward of 60^∘ S and between 20 and 40^∘ S and anomalous divergence between 40 and 60^∘ S. This pattern is mainly reproduced in the uniform SST warming experiment but with a smaller contribution to the two regions of anomalous EPF convergence from the rapid adjustment. Previous studies have demonstrated mechanisms for tropospheric warming to influence the stratospheric EPFD and residual circulation (e.g. Shepherd and McLandress, 2011), but the mechanism through which the rapid adjustment acts on EPFD in the upper stratosphere is less well understood. The radiative cooling in the stratosphere due to increased CO₂ is relatively uniform in latitude (Fels et al., 1980), so we do not expect large direct changes in zonal wind through thermal wind balance. However, the temperature response to CO₂ represents a weakening of the vertical temperature gradient, particularly in the upper stratosphere where the cooling is larger. The characteristics for wave propagation and refraction can be quantified using a measure of refractive index (e.g. Matsuno, 1970) that is dependent on the Brunt–Väisälä frequency ($N^{\mathrm{2}}=g/\mathit{\theta }(\mathrm{d}\mathit{\theta }/\mathrm{d}z)$). Hence, we hypothesize that the changes in background temperature structure due to the CO₂ radiative effects alter the propagation of Rossby waves, particularly in the upper stratosphere, and this leads to the changes in EPFD shown in Figs. 7 and 8.

Figure 8 As in Fig. 7, but for the JJA season.

The anomalous residual circulation is driven by both resolved and parameterized wave forcing. The seasonal parameterized wave forcing (NOGWD and OGWD) anomalies are shown in Figs. S3 and S4 for DJF and Figs. S5 and S6 for JJA. The peak changes in parameterized wave forcing are smaller than the anomalous resolved wave forcing by around a factor of 2. The anomalous NOGWD is mainly in the upper stratosphere and comes from the uniform SST warming. There is anomalous OGWD (Figs. S4 and S6) in the winter hemispheres near the edge of the polar vortex, which has comparable contributions from the rapid adjustment and the uniform SST warming.

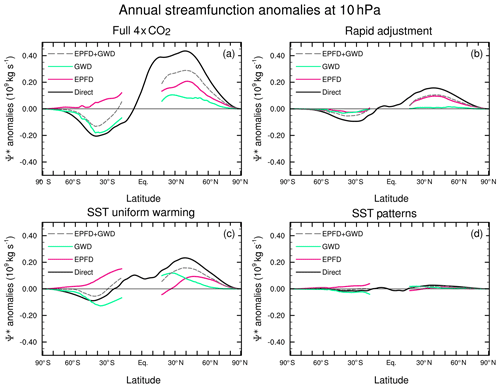
We now quantify the contributions of the different wave types to the anomalous mass circulation in the lower and upper stratosphere. Figures 9 and 10 show latitudinal profiles of the annual-mean mass streamfunction anomalies in each experiment at 70 and 10 hPa, respectively, along with the DCP inferred contributions from the resolved and parameterized components of the wave forcing. The DCP calculation for the total wave forcing underestimates the directly calculated maximum streamfunction anomaly in the model by around 20 %.

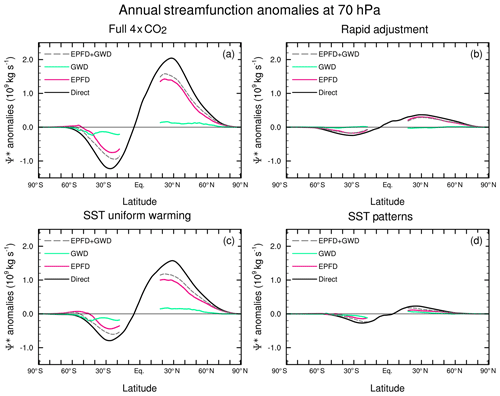
Figure 9 Annual-mean residual streamfunction anomalies (10⁹ kg s⁻¹) at 70 hPa with respect to the piControl simulation for the (a) 4×CO₂ (run B), (b) rapid adjustment (run C), (c) uniform SST warming (run D), and (d) SST pattern (run E) experiments. The black line shows the direct calculation, the downward control calculations for EPFD, OGWD + NOGWD, and their sum (EPFD + OGWD + NOGWD) are shown in magenta, green, and grey, respectively.

Figure 10 As in Fig. 9, but at 10 hPa.

In the lower stratosphere at 70 hPa, the estimated streamfunction anomalies from the total wave forcing in the full 4×CO₂ experiment come mainly (>80 %) from the resolved wave forcing (Fig. 9a), with a smaller and more homogeneous contribution from the parameterized wave drag. The resolved wave forcing explains almost all of the DCP estimated response in the rapid adjustment experiment (Fig. 9b) and most of it in the uniform SST warming (Fig. 9c) case. The component that contributes the smallest increase in streamfunction at 70 hPa, the SST pattern experiment (Fig. 8d), shows roughly equal contributions from parameterized and resolved wave forcing. The overall dominance of the resolved wave forcing for the strengthened BDC in the lower stratosphere is consistent with the larger changes in resolved wave drag in this region (Figs. 7 and 8) compared to the parameterized wave forcing changes in this region (Figs. S3–S6).

In the upper stratosphere (10 hPa), the full 4×CO₂ experiment shows contributions to the enhanced streamfunction from both resolved and parameterized wave forcing (Fig. 10a). In the NH, the EPFD contribution explains around two-thirds of the total DCP estimated streamfunction anomalies and GWD around one-third. The positive NH streamfunction anomaly from EPFD poleward of 30^∘ N comes from both the rapid adjustment (Fig. 10b) and the uniform SST warming (Fig. 10c). In contrast, the positive streamfunction anomaly in the upper stratosphere from parameterized wave drag comes mainly from the uniform SST warming (Fig. 10c).

In the SH, the results for the full experiment are somewhat more complex, with the major contribution to the enhanced poleward mass transport coming from GWD, which is partly offset by an opposite contribution from the EPFD. This positive SH streamfunction anomaly associated with EPFD comes mainly from the uniform SST warming (Fig. 10c), which also generates enhanced SH poleward transport via enhanced GWD. This increased poleward flow in the SH upper stratosphere is further increased by the rapid adjustment (Fig. 10b) with contributions from both resolved and parameterized wave drag. In both hemispheres, the SST pattern has little effect on the wave forcing in the upper stratosphere (Fig. 10d).

3.5 Uncertainty in global-mean SST response

Figure 11 summarizes the results by showing the annual-mean tropical upward mass flux anomalies in the different experiments at 70 hPa (Fig. 11a) and 10 hPa (Fig. 11b). Also shown are the mass flux anomalies from the high- and low-uniform-warming experiments (runs F and G), which span the spread in 4×CO₂ global-mean SST response across the CMIP5 models. In the lower branch of the BDC, the annual-mean tropical upward mass flux increases by 45 % in the full experiment compared to piControl (3.1×10⁹ kg s⁻¹). The uniform SST warming accounts for ∼70 % of this increase, with the rapid adjustment (∼20 %) and SST patterns (∼10 %) contributing the remainder in comparable amounts. The central estimates of the mass flux anomalies at 70 hPa in the three uniform SST warming (2.1, 3.4, 4.9 K) experiments are 1.4, 2.3, and 3.4×10⁹ kg s⁻¹, which gives an approximate linear scaling of 0.7×10⁹ kg s⁻¹ K⁻¹ (∼10 % K⁻¹). In the lower stratosphere, the uncertainty from the CMIP5 model spread in global-mean SST response to 4×CO₂ is larger than the contribution from the rapid adjustment and the SST pattern effect.

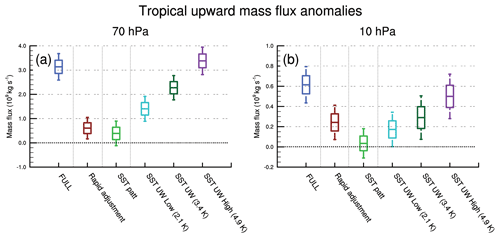
Figure 11 Annual-mean tropical upward mass flux anomalies (10⁹ kg s⁻¹) at (a) 70 hPa and (b) 10 hPa in the different perturbation experiments as labelled. The edges of the box plots indicate ±1 SD (standard deviation) of the interannual variability, and the whiskers indicate ±2 SD.

In the upper stratosphere at 10 hPa, the total mass flux increases by around 35 % in the full experiment (0.6×10⁹ kg s⁻¹). This increase comes almost equally from the rapid adjustment (∼40 %) and the uniform SST warming (∼45 %), with the remaining ∼15 % contribution coming from the SST pattern effect, though the latter is not statistically distinguishable from internal variability. The central estimates of mass flux anomalies at 10 hPa in the three uniform SST warming experiments are 0.17, 0.29, and 0.50×10⁹ kg s⁻¹, which gives an approximate linear scaling with global-mean SST of 0.11×10⁹ kg s⁻¹ K⁻¹ (∼7 % K⁻¹). In the upper stratosphere, the magnitude of the anomalous mass flux due to the rapid adjustment is therefore comparable to the uncertainty from the model spread in global-mean SST response to 4×CO₂.

4 Discussion and conclusions

We have performed idealized experiments with the HadGEM3-A model to decompose the long-term Brewer–Dobson circulation response to an abrupt quadrupling in CO₂ into three components: (1) a rapid atmospheric adjustment where CO₂ is added to the atmosphere but sea surface temperatures (SSTs) are held fixed; (2) a contribution from the global-average SST change; and (3) an SST pattern effect. The SST anomalies in response to the abrupt 4×CO₂ perturbation were derived from the CMIP5 multi-model ensemble. The multi-model annual-mean global-mean SST anomaly over the final 50 years of the CMIP5 abrupt 4×CO₂ runs is 3.4 K. The SST pattern (i.e. the local deviation from the global-mean value) shows relatively higher SST across the tropical oceans and most of the Northern Hemisphere and relatively cooler SST across much of the Southern Ocean and in the northern North Atlantic. The HadGEM3-A simulations are perturbed from a reference pre-industrial state, and sea ice concentrations are held fixed to enable a clean separation of the effects of SST without combining this with the potential effect of sea ice changes on the stratosphere (e.g. Kim et al., 2014).

In the tropical lower stratosphere, the 45 % increase in the annual-mean mass transport by the BDC under the full 4×CO₂ perturbation comes mainly (∼70 %) from the uniform SST warming consistent with the findings of Lin et al. (2015). The remainder comes from the rapid adjustment (∼20 %) and the SST pattern effect (∼10 %). The amplitude of the SST pattern effect on the mass transport in the lower stratosphere is broadly comparable to that found on interannual timescales associated with ENSO (Calvo et al., 2010; Simpson et al., 2011). Though note that while the SST pattern imposed here shows enhanced warming in the equatorial Pacific, by construction it contains a global structure, including relative warming across the tropical oceans and North Pacific and relative cooling in the Southern Ocean (Fig. 1c). In the upper stratosphere, where the deep branch of the BDC occurs, the increase in the BDC mass transport under abrupt 4×CO₂ comes from the rapid adjustment and the uniform SST warming in roughly equal measure. The results are consistent with studies that show an important role for the strengthening of the subtropical jets under climate change (e.g. Garcia and Randel, 2008; Lin and Fu, 2013; McLandress and Shepherd, 2009; Shepherd and McLandress, 2011), which in the decomposition performed here comes mainly from the uniform SST warming. However, our results also demonstrate that an increase in the BDC in the upper stratosphere comes mainly from the radiative cooling of the stratosphere by CO₂, as seen in the rapid adjustment component of the response. This means that in transient atmosphere–ocean abrupt 4×CO₂ experiments, there are expected to be different characteristic timescales for the BDC response. In the lower stratosphere, the timescale of the BDC response will be mainly determined by the rate of tropospheric warming and associated changes to upper-tropospheric heating and subtropical jet strength, while in the upper stratosphere there will be a fast timescale associated with the CO₂ radiative cooling and a slow timescale also tied to the tropospheric warming. The results therefore demonstrate the existence of two timescales in the response of the BDC to increasing CO₂, with the relative importance of each timescale for the long-term response being height dependent.

We further examined the effect of the uncertainty in global-mean SST response to increased CO₂, as a proxy for model spread in equilibrium climate sensitivity. The range in the global-mean SST response across the CMIP5 models is 2.1 to 4.9 K. Further experiments imposing these global uniform SST values show an increase in the lower stratosphere (70 hPa) upward mass flux of 1.4×10⁹ and 3.4×10⁹ kg s⁻¹, which can be compared to the increase of 2.3×10⁹ kg s⁻¹ in the multi-model mean global SST experiment. In the upper stratosphere (10 hPa), the upward mass flux change for uniform SST warming of 2.1 and 4.9 K is 0.17×10⁹ and 0.5×10⁹ kg s⁻¹, respectively, which can be compared to 0.29×10⁹ kg s⁻¹ in the multi-model mean global SST experiment. Therefore, in the lower stratosphere the contribution from the uniform SST warming and its uncertainty is larger than the rapid adjustment and SST pattern effects on the BDC in the lower stratosphere. However, in the upper stratosphere (10 hPa) the uncertainty in the magnitude of global-mean SST increase across models is comparable to the magnitude of the rapid adjustment effect on the BDC.

Using the tropical mass flux anomalies described above and the GSAT changes in the experiments given in Sect. 2.2, we calculate a linear dependence of the tropical upward mass flux on GSAT of 0.62×10⁹ kg s⁻¹ K⁻¹ (∼9 % K⁻¹) at 70 hPa and 0.10×10⁹ kg s⁻¹ K⁻¹ (∼6 % K⁻¹) at 10 hPa. Hardiman et al. (2014) examined CMIP5 models and calculated a multi-model mean trend in 70 hPa upward mass flux of 3.2 % per decade over 2006–2099 in the Representative Concentration Pathway 8.5 (RCP8.5) emissions scenario. The multi-model mean change in GSAT between 2081 and 2100 relative to 1986–2005 is 3.7 K in the RCP8.5 scenario (Collins et al., 2013). This gives an approximate multi-model mean GSAT trend for the 21st century of 0.35 K per decade. Dividing these two numbers gives an estimate for the relationship between 70 hPa mass flux and GSAT of ∼9 % K⁻¹. This is in almost exact agreement with our results, despite the different modelling approaches, though our estimate would be slightly larger if the contributions from the rapid adjustment and SST pattern effects, which are implicitly included in the simulations used by Hardiman et al. (2014), were accounted for. The comparison is further complicated by the projected reduction in the BDC due to ozone recovery (e.g. Oman et al., 2009), which offsets part of the GHG-driven increase over the 21st century; this effect is also included in the 21st century scenario simulations used by Hardiman et al. (2014), and, if removed, this would presumably make the inferred relationship to GSAT larger than the ∼9 % K⁻¹ estimated above based on the CMIP5 RCP8.5 scenario.

The CO₂ perturbation applied here is large compared to projected CO₂ concentrations during the 21st century based on current mitigation commitments under the United Nations Framework Convention on Climate Change (UNFCCC) 2015 Paris Agreement. For a smaller increase in CO₂, the rapid adjustment and uniform SST warming contributions are expected to be smaller; in this case the SST pattern effect would become proportionately more important. Our experiments have neglected any feedbacks that induce stratospheric ozone changes. It has been shown that the ozone response to 4×CO₂ affects the zonal-mean extratropical circulation (Chiodo and Polvani, 2017); it would be interesting to also examine the effects of ozone on the BDC in the future. The experiments are designed to study the long-term centennial response to an abrupt quadrupling of CO₂, and they have only been performed with one model. The model contains mean state biases that could affect some of the details of the responses described here. Studies with other coupled atmosphere–ocean models and those that examine the transient response of the BDC to CO₂ would therefore be insightful.