Simulating record-shattering cold winters of the beginning of the 21st century in France

Extreme cold winter temperatures in Europe have huge societal impacts. Being able to simulate worst-case scenarios for such events for present and future climates is hence crucial for short- and long-term adaptation. In this paper, we are interested in persistent cold events, whose probability will decrease with climate change. Large ensembles of simulations allow us to better analyse the mechanisms and characteristics of such events but can require significant computational resources. Rather than simulating very large ensembles of normal climate trajectories, rare-event algorithms allow the sampling of the tail of distributions more efficiently. Such algorithms have been applied to simulate extreme heat waves. They have emphasized the role of atmospheric circulation in such extremes. The goal of this study is to evaluate the dynamics of extreme cold spells simulated by a rare-event algorithm. We focus on cold winter temperatures that have occurred in France from 1950 to 2021. We investigate winter mean temperatures (December, January and February) and identify a record-shattering event in 1963. We find that although the frequency of extreme cold spells decreases with time, their intensity is stationary. We apply a stochastic weather generator (SWG) approach with importance sampling to simulate the coldest winters that could occur in a factual and counterfactual climate. We thus simulate ensembles of the worst winter cold spells that are consistent with reanalysis data. We find that a few simulations reach colder temperatures than the historical record-shattering event of 1963. This shows that present-day conditions can trigger winters as cold as that record in spite of global warming. The atmospheric circulation that prevails during those events is analysed and compared to the observed circulation during the record-breaking events, showing no main change in the mechanisms leading to this type of extreme event.

1 Introduction

Winter cold spells in the midlatitudes have had wide-ranging impacts, affecting agriculture (Trnka et al., 2011; Vogel et al., 2019), health (Gasparrini et al., 2015; Smith and Sheridan, 2019), infrastructure (Chang et al., 2007) or energy systems (Añel et al., 2017; Bessec and Fouquau, 2008; Van Der Wiel et al., 2019). Cold events are expected to decrease in terms of both intensity and frequency with climate change in most regions of the world (Seneviratne et al., 2021), which could lead to an overall reduction in their impacts. In recent decades a decrease in intensity has been recorded in the western European region (Cattiaux et al., 2010; Seneviratne et al., 2021; Smith and Sheridan, 2020; Van Oldenborgh et al., 2019). But even if their probability decreases, extreme cold winter events still occur and can cause major disruptions, like winter 2010 in western Europe (Cattiaux et al., 2010) or the cold snap of February 2021 in Texas (Doss-Gollin et al., 2021). Winter 2010 was perceived as extremely cold in Europe and raised questions in the media and from the general public about the occurrence of extreme cold events under climate change. Cattiaux et al. (2010) showed that winter 2010 was actually not as extreme as records of the previous decades and would have been much more extreme given the same atmospheric conditions if it had occurred in a past climate with a lower influence of climate change. This is consistent with the general upward trend in winter minimum temperatures, as shown in Fig. 1a for various lengths of cold episodes.

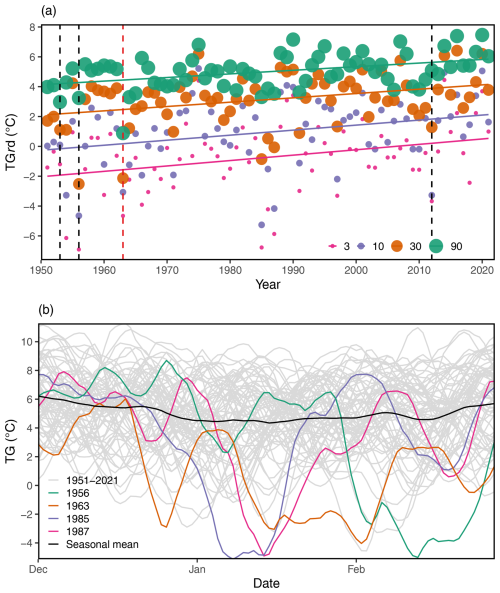
Figure 1 (a) Minima of winter temperature over DJF for four event durations in continental France. For each winter we compute the n d running mean of daily mean temperature (TG) for $n\in \mathit{\{}\mathrm{3},\mathrm{10},\mathrm{30},\mathrm{90}\mathit{\}}$ d and select the minimum value. The coloured lines are linear regressions of the temperature averages. The vertical dashed red line outlines 1963 (the coldest winter in France). The vertical dashed black lines outline the winters of 1953, 1956 and 2012. (b) Time series of DJF 7 d running mean TG from 1950 to 2021 in continental France. The curves in colour are for the 4 coldest years (1956, 1963, 1985 and 1987), and the black curve is for the seasonal mean computed over 1951–2021.

However, uncertainties remain about the potential dynamical effects of climate change on severe winter midlatitude weather (Cohen et al., 2020; Horton et al., 2015; Overland et al., 2016; Shepherd, 2015). Arctic amplification (AA) is a mechanism that may lead to an increase in severe winter weather in the midlatitudes (Cohen et al., 2014; Francis et al., 2018; Francis and Vavrus, 2012; Vavrus, 2018), but its potential effect is intertwined with other hemispheric drivers of decadal variability, and the quantification of its influence remains debated (Blackport and Screen, 2020; Cohen et al., 2020; Francis, 2017). Several studies have also shown that winter warming and winter anomaly trends are not as large as the upward trend in summer warm anomalies in the Northern Hemisphere (Robeson et al., 2014) and more specifically in France (Ribes et al., 2022). The decrease in winter cold spells would consequently not be as significant as the increase in summer heat waves.

The goal of this study is to assess whether we could simulate a winter as cold as a 20th century like cold winter record using present-day climate conditions and how their intensity and mechanisms are affected by climate change. We aim to build storylines of a worst-case winter scenario in France for the present decades (here, worst-case scenario is meant to identify conditions leading to events that are colder than have already been observed). Storylines are a “physically self-consistent unfolding of past events or of plausible future events or pathways”. They aim to better understand the driving factors of high-impact events with deep uncertainties in a way that is more understandable by people than a purely probability-based risk assessment and explore the “boundaries of plausibility” (Shepherd et al., 2018).

To assess worst-case-scenario winter temperatures in France, we use the winter of 1962–1963 (hereafter referred to as winter 1963) as a reference event. Winter 1963 yielded an exceptionally low mean temperature anomaly over December, January and February (DJF) of −3.4σ below the seasonal average (Fig. 1a). The year 1963 was also extreme in its spatial scale, with negative temperatures covering most of Europe (Greatbatch et al., 2015; Hirschi and Sinha, 2007; O'Connor, 1963). This led to exceptional weather across the continent: large lakes, like Lake Constance or Lake Zurich, froze entirely, and widespread and persistent snow coverage was observed in the British Isles. According to the (), it was the coldest winter since 1740 in the United Kingdom. In France, the first intense cold wave occurred at the end of December, lasting 1 week, followed by a second, more prolonged cold wave with negative daily mean temperature over France from 11 January to 6 February (Fig. 1b). Winter 1963 was associated with a negative North Atlantic Oscillation (NAO) index, indicating a lower-than-normal pressure difference between the Iceland low- and Azores high-pressure systems (Cattiaux et al., 2010; Greatbatch et al., 2015). A persistent negative NAO phase is usually associated with the development of North Atlantic atmospheric blocking (Shabbar et al., 2001) and a weakening of the westerlies, allowing outbreaks of cold air coming from the Arctic or Russia into western Europe (Greatbatch, 2000; Hurrell et al., 2003).

According to the definition of Fischer et al. (2021), winter 1963 was a record-shattering event in France; i.e. the record for low temperatures was broken by a large margin of several standard deviations (Fig. 1a). Therefore, winter 1963 was an extremely low probability event, even considering the colder climate (than in the 21st century) in which it occurred. If the average winter temperature follows a Gaussian distribution, this corresponds to a return period larger than 10³ years, which is longer than the observational periods. The objective of this study is to examine

1. whether a winter as cold as that of 1963 can be generated by a statistical model given information that excludes that specific winter and

2. whether such a winter can still be simulated given climate information from recent decades, during which the climate has been warmer.

Simulating an ensemble of events whose return period is larger than the observational period or the typical length of climate model simulations requires intensive computing resources. For instance it corresponds to ≈ 250 years for simulations from the Coupled Model Intercomparison Project phase 6 (CMIP6; Eyring et al., 2016) by concatenating “historical” (1850–2014) and “scenario” (2015–2100) simulations. Even if a large ensemble of simulations is considered (e.g. up to ≈ 50 ensemble members in the CMIP6 archive), the 2000–2050 period would yield $\approx \mathrm{50}\times \mathrm{50}$ years of simulations (e.g. with the CESM2 model; Danabasoglu et al., 2020), which would lead to two to three examples of events similar to the winter of 1963, with a return period of 10³ years. Several methods based on principles of statistical physics have been developed to provide fast and realistic simulations of large values of atmospheric variables. Rare-event algorithms using importance sampling (e.g. Ragone et al., 2018) have been designed to specifically simulate extreme heat waves from a climate model. A simplified simulation approach was proposed by Gessner et al. (2021) by carefully selecting trajectories of a climate model that lead to lower temperatures over a given region (Germany). An alternative approach is based on stochastic weather generators (SWGs). SWGs are Markov processes used to generate large ensembles of atmospheric trajectories with realistic statistical properties at a low computational cost (Ailliot et al., 2015). Yiou and Jézéquel (2020) combined an SWG based on analogues of circulation (i.e. days with a similar atmospheric simulation) developed by Yiou (2014) and the importance sampling principle by Ragone and Bouchet (2021) to specifically simulate extreme summer heat waves from analogues of circulation. This method allows for the simulation of an ensemble of physically consistent trajectories of extreme events at a very low computational cost. In this study, we adapt the analogue-based stochastic weather generator with importance sampling of Yiou and Déandréis (2019) to the simulation of low-likelihood, high-impact extreme winter events.

We use SWG simulations based on reanalysis data in order to assess the intensity of the worst-case winter scenario in France in a counterfactual period (with a lower influence of climate change) and a factual period representing the present-day climate with a more detectable influence of climate change. Therefore, we examine how climate change affects the intensity of the worst-case cold winters that can hit France and to what extent extreme cold winters like 1963 could still be possible in the present-day climate.

A study by Sippel et al. (2024) has conducted a similar analysis of winter 1963 for Germany, using both ensemble boosting of the CESM2-LE model (Rodgers et al., 2021) and the SWG used in this paper. This paper provided an investigation of such winters focusing on France and a more in-depth analysis of the use of the analogue SWG. The present paper details the SWG methodology and shows an application for France.

The paper is organized as follows. Section 2 presents the datasets used in the paper and details the analogue-based stochastic weather generator model for sampling cold winters. Section 3 shows the results of the simulations of extreme winters. Section 4 discusses the main results of the study.

2 Data and methods

2.1 Data

Daily mean surface temperature (TG) data were obtained from the fifth version (ERA5) of the atmospheric reanalysis of the European Centre for Medium-Range Weather Forecasts (ECMWF) (Hersbach et al., 2020). Data from 1950 to 2021 have been retrieved with a spatial resolution of 0.25°×0.25°. Daily temperature fields have been averaged over the smallest spatial domain including metropolitan France (42–52° N, 5° W–9° E). ERA5 was chosen for its large time coverage and its high horizontal resolution of 0.25°.

We compute running averages of temperature for four event durations (r=3, 10, 30 and 90 d) and determine the minimum value for each winter (from December to February). This corresponds to identifying the coldest r d period for each year, or TGrd. For an even value of r, we compute the minimum over all time steps t:

$$\begin{array}{}\text{(1)}& \mathrm{TG}r{\mathrm{d}}_t={\displaystyle \frac{\mathrm{1}}{r}}\sum _{i=-r/\mathrm{2}}^{(r/\mathrm{2})-\mathrm{1}}{\mathrm{TG}}_{t+i},\end{array}$$

where TG_t is the daily average temperature at time step t. For an odd value of r, the equivalent sum is centred around r. Figure 1a shows the variations in the TGrd time series for France. Additional information on the associated distributions is shown in Appendix A. We observe an upward trend in TGrd at the four event durations r. The records for each event duration occurred before 1990. However, extreme cold events still happened in the 21st century: winter 2012 witnessed the fifth-coldest 10 d and the eighth-coldest 3 d cold spells of the 1950–2021 period. In the 30 d event duration, February 1956 and January 1963 were two exceptional events, with temperature anomalies relative to the 1950–2021 trend of −2.9σ and −2.8σ, respectively (see dashed black lines in Fig. 1a). One event stands out in the 90 d winter temperatures: winter 1963 is at 3.7σ from the trend of winter mean temperatures and 2.2σ under the second-coldest winter in 1950–2021, winter 1952–1953. For conciseness, this paper focuses on TG90d, i.e. DJF average temperatures. This assumption of the distribution of TGrd to be Gaussian is experimentally justified in Appendix A.

For the computation of analogues of circulation, we use daily geopotential height at 500 hPa (z₅₀₀) from the ERA5 reanalysis from 1950 to 2021. z₅₀₀ was chosen over sea level pressure (SLP) because of its lower susceptibility to perturbations from the surface roughness and its common use in weather regime studies (Corti et al., 1999; Yiou and Nogaj, 2004; Jézéquel et al., 2018; Dawson et al., 2012). Jézéquel et al. (2018) also showed that it was better suited to simulate temperature anomalies, although that study investigated warm temperatures. z₅₀₀ data were regridded on a 1°×1° grid to reduce computation time since a higher resolution has little impact on the analogue calculation because of the smooth spatial variability in the z₅₀₀ fields. We considered the z₅₀₀ field over the North Atlantic region (30–70° N, 20° W–30° E) to compute circulation analogues. This domain offers a compromise between spatial coverage large enough to study the role of the synoptic circulation but small enough to not drown out the signal in the too complex hemispheric circulation.

2.2 Analogues of circulation

We first compute a database of analogues of circulation following the procedure of Yiou and Jézéquel (2020). For a given day t, we compute the Euclidean distance of the z₅₀₀ fields between t and all days t^′ that are not in the same winter and within a calendar distance to t of less than 30 d (i.e. the difference in days between 2 d, regardless of the year). The K analogue days of t are the K d for which the distance from t is the smallest. We chose K=20 analogues, as advocated in previous studies (Platzer et al., 2021).

The circulation analogues were computed using the Blackswan Web Processing Service (Hempelmann et al., 2018). We consider three different analogue datasets depending on the time period in which the analogues are selected:

1. 1951–2021 – the whole length of available ERA5 data;

2. 1951–1999 – the past period as a counterfactual scenario, with less influence of anthropogenic climate change and

3. 1972–2021 – the present period as a factual scenario, with a significant signal from climate change.

The analogue periods were chosen to have sufficient length to be representative of all the possible states of the atmospheric patterns while being characteristic of climate periods that are significantly different. We were constrained by the length of the ERA5 data available (only 71 years). Therefore we chose a compromise between analogue depth and low overlap by considering two 50-year periods (1950–1999 and 1972–2021). The distribution of analogue years and their quality is detailed in Appendix B.

2.3 Stochastic weather generator and importance sampling

The analogue-based stochastic weather generator (hereafter referred to as SWG) developed by Yiou (2014) uses stochastic reshuffling of daily atmospheric fields to generate atmospherically consistent alternative trajectories of climate events. This algorithm was adapted by Yiou and Jézéquel (2020) to simulate extreme heat waves using the principle of importance sampling. The goal is to simulate L d trajectories of a model while maximizing an observable variable (e.g. local temperature). Here we focus on a modified version of the dynamic type of simulations developed by Yiou (2014), which computes alternative atmospheric trajectories starting with the same initial conditions as an observed event. Each time step is the combination of an atmospheric circulation (characterized by z₅₀₀) and a variable of interest, such as temperature. The SWG starts at a given initial condition and goes from one time step to the next using analogues of circulation according to the process described hereafter. The resulting simulation is a constrained reshuffling of days of the input dataset. We start at an initial condition t₀, which thus constitutes the first time step of the simulation. To simulate temperature for the day after t₀ ($t=t_{\mathrm{0}}+\mathrm{1}$), we randomly pick one analogue among the K best analogues of the observed z₅₀₀ field on day t₀+1. The geopotential height at 500 hPa (z₅₀₀) and the 2 m temperature (TG) fields of this analogue day constitute the simulated day t^′. For the next time step, t is replaced by $t^{\prime }+\mathrm{1}$, the day following t^′. This random process is repeated sequentially for L time steps, the length of the simulation. This defines a Markov chain of TG, with latent states provided by the analogues of z₅₀₀.

At each time step, the selection of the analogue day follows several constraints and weights controlled by the parameters that are described hereafter. To better follow the seasonal cycle of the simulated season, we use K weights ${\mathit{\omega }}_{\mathrm{cal}}^{\left(k\right)}$ ($k\in \mathit{\{}\mathrm{1},\mathrm{\dots },K\mathit{\}}$) on the analogue selection that depend on a parameter α_cal, which favours analogue days that are closest to the calendar date (i.e. the day of the year, regardless of the year) of time step t:

$$\begin{array}{}\text{(2)}& {\mathit{\omega }}_{\mathrm{cal}}^{\left(k\right)}=A_{\mathrm{cal}}{e}^{-{\mathit{\alpha }}_{\mathrm{cal}}{d}_k},\end{array}$$

where A_cal is a normalizing constant, α_cal≥0 is the calendar weight, and d_k is the number of calendar days between the kth analogue day and t. The resulting seasonal cycle of the SWG is shown in Appendix C.

To favour the simulation of the most extreme events, importance sampling weights ${\mathit{\omega }}_T^{\left(k\right)}$ are introduced, with a control parameter α_T≥0. When the value of α_T increases, the stochastic weather generator favours analogue days with extreme temperatures. The K analogues of t are sorted in ascending order of temperature with ranks $R_k(k\in \mathit{\{}\mathrm{1},\mathrm{\dots },K\mathit{\left\}}\right)$ such that the coldest analogue day has a rank of 1. Hence the weight associated with the kth analogue day of t is

$$\begin{array}{}\text{(3)}& {\mathit{\omega }}_T^{\left(k\right)}=A_T{e}^{-{\mathit{\alpha }}_T{R}_k},\end{array}$$

where A_T is a normalizing constant, α_T is the importance sampling weight and R_k is the rank (in ascending order) of the kth analogue day among the K analogues. If α_T=0, there is no importance sampling, and the SWG is the same as in (Yiou, 2014). As explained by Yiou and Jézéquel (2020), using the ranks of temperature instead of their absolute values eliminates the need to re-scale variables and allows for an interpretation independent of the units of the variables. It also ensures that simulations are biased in the same way, as importance sampling weights are the same at each time step (the ranks are simply all integers between 1 and K=20).

The SWG with importance sampling is obtained by combining the weights on the calendar and importance sampling. The kth analogue day of day t has a probability of

$$\begin{array}{}\text{(4)}& {\mathit{\omega }}_k=A{e}^{-{\mathit{\alpha }}_{\mathrm{cal}}{d}_k}{e}^{-{\mathit{\alpha }}_T{R}_k},\end{array}$$

where A is a normalizing constant such that ${\sum }_{k=\mathrm{1}}^K{\mathit{\omega }}_k=\mathrm{1}$.

2.4 SWG configurations

We have refined the original methodology proposed by Yiou and Jézéquel (2020) by introducing a new approach for simulating trajectories with the analogue-based SWG. Our primary objective is to generate extreme winter events that are characteristic of specific climate periods, essentially seeking to estimate the extremes attainable within a climate state characterized by a defined level of warming. Given a reference record-shattering event, we want to assess the likelihood of a similar event occurring within a given climate period, without specific information about the event itself.

To achieve this objective, we have made a crucial adjustment of the original SWG configuration (configuration 1, which considers the entire dataset in the simulations). This new configuration (configuration 2) no longer considers analogues that coincide with the reference event. At each time step, the selection process is based on the K best analogues, but the weights ω_k of analogue days that fall within the observed event are set to zero. For example, if we initiate a simulation on 1 December 1962 spanning L=90 d, all analogue days falling between 1 December 1962 and 1 March 1963 are excluded from consideration in the simulation. Days of the same year were already excluded during the analogue computation process, but they can still be selected in simulations as analogues of days in other years. This procedural adjustment ensures that our simulations are solely driven by the initial conditions and the state of the climate and do not rely on any specific information pertaining to the observed event (apart from the first day). In other words, we are assessing whether a record-shattering event of 90 d can be inferred from information related to less extreme events.

We also adapted this stochastic weather generator from the one in Yiou and Jézéquel (2020), which was designed to simulate summer heat waves, to the version used in this analysis tailored for simulating winter cold spells. Consequently, the importance sampling weights now favour the coldest analogues instead of the warmest ones.

2.5 Consistency of SWG trajectories

To control the consistency of the atmospheric trajectories produced by the SWG, we compute the derivatives of the resulting time series of z₅₀₀ and temperature from first-order differences. The derivatives are compared on the one hand to the derivatives obtained in the observed winter and on the other hand to the time series computed by randomly picked winter days from the ERA5 dataset. The results are shown in Fig. 2a and b. Because of the approximation by analogues, the SWG loses continuity, which appears in the derivative calculation. But the ratio of the z₅₀₀ derivative standard deviation between the simulations and the observations is ≈1.2, which is far less than the same ratio computed from random time series (≈3.5). This illustrates that the SWG atmospheric trajectories are mathematically consistent and realistic. The same analysis for the daily temperature derivative shows a larger difference between the ERA5 reanalysis and the SWG simulations. This can be explained by the fact that the analogue SWG trajectories are primarily based on an atmospheric trajectory constraint (and not a constraint on temperature). The resulting temperature time series are still more consistent compared to time series of random winter days (the ratios of standard deviation derivatives with the reanalysis are ≈1.8 and ≈3.2, respectively). Therefore, the short-term variability (i.e. a few days) is deemed to be relevant from a mathematical point of view.

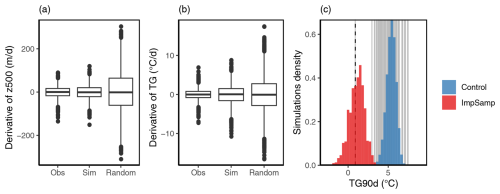
Figure 2 Daily derivatives of z₅₀₀ (in m d⁻¹) (a) and TG (in °C d⁻¹) (b) for winters in ERA5, in the SWG simulations and in random trajectories. The boxes of the boxplots indicate the median (q50); the lower and upper hinges indicate the first (q25) and third (q75) quartiles. The upper whiskers indicate min[max(T), q75 + 1.5 ⋅ (q75 − q25)]. The lower whiskers have a symmetric formulation. The points are the outlying values that are above or below the defined whiskers. (c) Normalized distribution of the TG90d of 1000 SWG simulations with α_cal=0.5 (red histogram, with importance sampling) and 10⁷ SWG simulations with α_cal=0 (blue histogram, without importance sampling). The vertical grey lines display the observed TG90d in ERA5. The dashed black line outlines the winter 1963 value.

Finally, we compare the mean temperatures of 1000 SWG trajectories with α_T set to 0.5 to the mean temperatures of 10⁷ control SWG trajectories with α_T set to 0 (i.e. without importance sampling) and to analogues in 1950–1999 (Fig. 2c). In the control simulations, the SWG covers the range of observed winter TG90d, apart from extreme values in the tail of the distribution, as in winter 1963. The median of simulations with importance sampling is close to the coldest control simulation. The SWG with importance sampling simulates extreme events in the tail of the distribution and is able to reach values on the same order of magnitude as winter 1963. The difficulty of obtaining winters as cold as 1963 without importance sampling shows the added value of this method for record-shattering events. The resulting distributions are comparable to the ones obtained for heat waves with a rare-event algorithm by Ragone and Bouchet (2021) and a control simulation of a climate model.

We verify in Appendix B that the selection of analogues does not yield obvious biases towards the earlier parts of each analogue period and that the quality of analogues is stationary in time across the two periods. Appendix C compares the climatological variations in the SWG without importance sampling to the original ERA5 data.

2.6 Protocol

First we tune the α_T and α_cal parameters for winter DJF simulations. We simulated ensembles of trajectories of 90 d starting on 1 December of each year, with different values of the parameter α_cal. Figure 3a shows the percentage of simulations for which the last day of the simulation falls after 15 February. If the calendar weight value is too small (e.g. α_cal=1), fewer than half of the simulations end with a calendar day after 15 February. This means that the trajectories of the simulated events with α_cal=1 are less consistent with the seasonal cycle. With an α_cal parameter greater than 5, more than 75 % of the simulations have their last day falling after 15 February. Therefore we use α_cal=5 in the following.

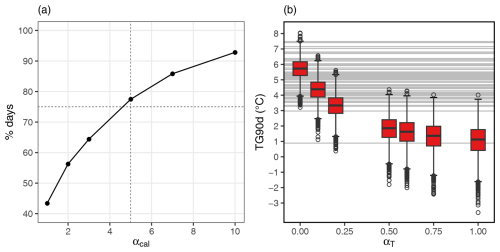
Figure 3 (a) Percentage of simulations of extreme winters for which the last day falls after 15 February as a function of the α_cal parameter. (b) Temperature (TG) distribution of 100 simulations (configuration 2) for each winter between 1950–1951 and 2020–2021 ($\mathrm{100}\times \mathrm{70}=\mathrm{7000}$ simulations total per boxplot) done for various values of the α_T parameter (${\mathit{\alpha }}_T\in \mathit{\{}\mathrm{0},\mathrm{0.1},\mathrm{0.2},\mathrm{0.5},\mathrm{0.75},\mathrm{1}\mathit{\}}$). Horizontal lines represent the winter mean temperature of each winter from 1950–1951 to 2020–2021 in ERA5 data. Boxplots are computed as in Fig. 2a.

We run the SWG with parameter values ${\mathit{\alpha }}_T\in \mathit{\{}\mathrm{0},\mathrm{0.1},\mathrm{0.2},\mathrm{0.5},\mathrm{0.75},\mathrm{1}\mathit{\}}$ starting on each 1 December, between 1950 and 2021. Figure 3b shows that for α_T=0, the SWG simulates events covering the range of winter mean temperatures from 1950–1951 to 2020–2021 apart from winter 1962–1963. For α_T=0.2, a few outlier simulations reach winter 1963 temperatures. A value of α_T greater than 0.5 allows the simulation of a greater proportion of extreme events. The difference for α_T greater than 0.5 being less significant, we chose for the following α_T=0.5.

To compare the configuration of the SWG excluding information from the event of reference to the previous configuration of Yiou and Jézéquel (2020), we use both to simulate the worst-case winter scenario from 1950 to 2021. For each winter from 1950 to 2021, the simulation starts at t₀ – 1 December – and runs for L=90 d over DJF (December, January and February). n=100 simulations are run per winter year; hence 100×71 events are simulated for each experiment.

Then we focus on the record-shattering event of winter 1963. Winter 1963 being our reference as a record-shattering event, we simulate alternative extreme winters in the counterfactual and factual climates without using the information from winter 1963 to evaluate to what extent such a winter can be extrapolated from available data in both climate periods. Simulations are also made using the two sets of analogues – the counterfactual and factual periods. Hence we simulate winters that could have occurred in the selected analogue period. This allows the simulation of worst-case events from the same initial conditions but considering different climate states. We run n=1000 simulations starting on 1 December 1962, using as previously the factual and counterfactual sets of analogues. This allows us to have a wider ensemble of possible winter temperatures starting from the initial conditions of winter 1963.

3 Results

3.1 Sensitivity to SWG configurations

In this subsection, we simulate cold winters of 90 d starting on 1 December of each year from 1950 to 2021. Analogues can be selected in any year from 1950 to 2021. We evaluate the impact of the possibility of sampling analogues from the reference event on the winter average temperature: the SWG configuration in Yiou and Jézéquel (2020) versus the one in the present paper.

Figure 4 shows the results of simulations from 1951 to 2021 using SWG configuration 1 (Fig. 4a) and SWG configuration 2 (Fig. 4b) in Sect. 2, with analogues sampled in 1950–2021. The SWG successfully simulates extremely cold winters, with simulations being 3.9 °C (Fig. 4a) and 3.1°C (Fig. 4b) colder overall compared to the long-term mean of ERA5 temperatures. Moreover, 40 % of all simulations reach a mean temperature as cold as the 1963 record with configuration 1, while only 13 % of them are as cold when using configuration 2.

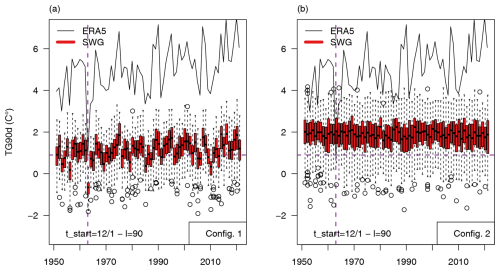
Figure 4 Results of 100 SWG simulations from winter 1950–1951 to winter 2020–2021 with configuration 1 (a) and configuration 2 (b). The continuous black line represents the time series of the winter mean 2 m temperature over France from the ERA5 data. The boxplots represent the ensemble variability in the simulations for each year. The vertical dashed purple line highlights winter 1963, while the horizontal dashed purple line shows the mean temperature of the same winter.

The variability in the simulations performed with configuration 1 follows the variability in historical winter temperatures closely due to the possibility of selecting analogues falling in the observed event with this configuration. The medians of simulations made with configuration 1 are highly correlated (r=0.88) to the observed temperatures. With configuration 2, there is no correlation between the median of simulations and the observed temperature. This is a consequence of the fact that configuration 2 does not use information from the observed event apart from the initial conditions. The simulation length of 90 d being longer than the decorrelation time of atmospheric dynamics, the resulting events should not be highly influenced by their initial conditions. The standard deviation of the medians of the boxplots obtained with configuration 2 is also very low: 0.15 °C compared to the 0.44 °C obtained with configuration 1. This is coherent with the chaotic internal variability in the climate system, resulting in simulated events being representative of the climate analogue period used rather than the initial conditions.

The mean of the boxplot median is also higher by 0.77 °C with configuration 2 compared to configuration 1, which can be explained by the fact that configuration 1 allows more days to be selected during the importance sampling process, so the coldest days can be selected intentionally during the simulations, while some analogue days are excluded when using configuration 2.

3.2 Focus on winter 1963

In this subsection, we simulate winters starting on 1 December 1962 and consider circulation analogues in the counterfactual and factual periods. We simulate 1000 winters that could have been in 1962–1963, with z₅₀₀ analogues in two periods. Figure 5a focuses on those simulations for both the factual and counterfactual analogue periods. The first quartile of simulations does not reach 1963 mean values in both the factual and counterfactual periods (boxplots in Fig. 5a). The year 1963 was already a very rare event in the 1950–1999 climate but remains reachable using only 1971–2021 analogues in a climate with more global warming. The observed increase in mean winter temperatures between the counterfactual and factual periods is not reproduced if we consider extreme winters as simulated by the SWG, even if we exclude winter 1963 from the counterfactual period (configuration 2). We observe an increase of 0.44 °C in TG90d between the two periods, while the difference is only 0.13 °C between the two ensembles of extreme winters. In other words, extremely cold winters do not warm at the same rate as winter mean temperatures.

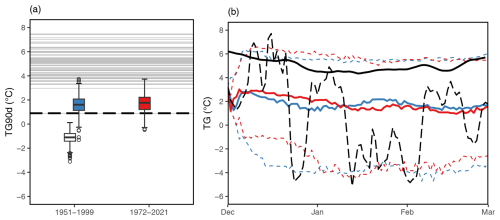
Figure 5 (a) Temperature (TG) distribution of 1000 SWG simulations of winter 1963 with analogues from 1951–1999 or 1972–2021 in ERA5 data using configuration 1 (white boxplot) and configuration 2 (colour-filled boxplots). Horizontal lines represent the winter mean temperature of each winter from 1950 to 2021 in ERA5 data. The dashed black line is the value that was observed in 1962–1963. (b) Time series of the 7 d running mean of daily mean temperatures for winter 1963 (dashed black line), SWG median (plain line), q05 and q95 (dashed lines) temperatures of the 1000 1962–1963 simulations with configuration 2 using 1950–1999 analogues (blue lines) and 1972–2021 analogues (red lines), and the seasonal cycle as computed from 1950–2021 (plain black line).

Figure 5b summarizes the time series of daily average temperatures associated with winter 1963 simulations. The temperatures of winter 1963 are below the seasonal cycle for most of the season. The temperatures of simulated events for both the factual and counterfactual periods are also overall below the seasonal mean for the whole length of the event. The median fluctuates around 2 °C, while the 5th percentile of all simulations reaches −5 °C during most of the winter. The 95th percentile stays under 2 °C above the seasonal average, while the 5th percentile reaches −4 °C during most of the event, which corresponds to the coldest daily mean temperatures observed in 1963. Overall the range of daily winter temperatures as simulated for extreme winter temperatures in the factual and counterfactual periods matches the range of daily mean temperatures observed in the reference event in 1963. Hence a winter like the one of 1962–1963, even with a low probability, can still occur using data from the warmer climate of the 21st century. We find that the likelihood of such cold winters barely decreases with time, as the distributions of simulated temperatures are very similar for the two analogue periods.

3.3 Atmospheric dynamics during winter 1963

During winter 1963, a strong and persistent anticyclonic anomaly prevailed over Iceland. It was associated with a negative z₅₀₀ anomaly over continental Europe, the Azores and the glacial Arctic Ocean, leading to a weakening of the westerlies and advection of cold air from the Arctic (Fig. 6a).

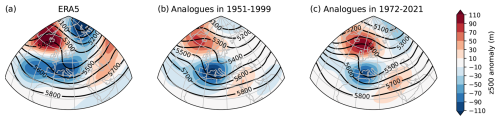
Figure 6 Absolute values (contours, in m) and anomalies (in m) with respect to 1950–2021 (shaded areas) of the 500 hPa geopotential height (z₅₀₀) average over DJF for winter 1963 as observed in ERA5 (a) and simulated by the SWG with counterfactual (b) and factual (c) analogues using configuration 2 (sine data). For the simulations, the composite maps are computed from the coldest 10 % of simulations among the 1000 (i.e. 100 simulations per map).

Here, we compute the composites of z₅₀₀ and z₅₀₀ anomalies over a region that is larger than the region for which the analogues are obtained. The z₅₀₀ composite over DJF does not correspond directly to a North Atlantic weather pattern (the negative phase of the North Atlantic Oscillation (NAO)), as, for instance, obtained by Cattiaux et al. (2010). The low over Europe is located more to the east than for an NAO− weather pattern, while the positive z₅₀₀ anomaly over Iceland is located more to the north than it would be in an Atlantic Ridge weather regime. The respective positive and negative z₅₀₀ anomalies over Iceland and the Azores are, however, characteristic of NAO−, which is often, even if not systematically, an indicator of colder-than-usual winter temperatures over Europe (Hirschi and Sinha, 2007).

The z₅₀₀ anomalies of SWG simulations for winter 1963 are spatially smoother than the ERA5 field for the same winter. This can be explained by the fact that the map is averaged over 100 (10 % of 1000 simulations) different simulations and that simulations are less auto-correlated than observed events would be, thus having more spatial variability. Hence, we compute the z₅₀₀ and z₅₀₀ anomaly composites of SWG simulations for the coldest 10 % of members of the ensemble starting on 1 December 1962. For comparison purposes with winter 1963, this selection is reasonable because 75 % of simulations are warmer than this record event (Fig. 5a), and we want to focus on the coldest members of the ensemble. Appendix D also shows that the average maps are representative of individual events. We find that the pattern of a strong negative anomaly over western Europe and a positive anomaly over Iceland is still reflected in the coldest 10 % of events simulated with the SWG in both the counterfactual (Fig. 6b) and factual (Fig. 6c) simulations. The intensity and position of the z₅₀₀ low over the Barents Sea and the z₅₀₀ high over western Russia, as seen in ERA5, seem to have a lower contribution to the intensity of the event, as they are weaker and less marked in the SWG-simulated events.

4 Conclusions

This paper presents the application of an analogue stochastic weather generator to simulate ensembles of extreme cold winters in continental France. We adapted the method developed by Yiou and Jézéquel (2020) (to simulate extreme heat waves) to the simulation of extreme cold events. In particular, this paper explicitly addresses the question of simulating the most extreme winter without using information from the observed record. The paper displays a proof of concept using ERA5 data for the simulation of extreme winter temperatures in France between 1950 and 2021.

The SWG for the simulation of extreme cold spells inherits some of the technical caveats already pointed out by Yiou and Jézéquel (2020) for the simulation of extreme heat waves. This SWG method is limited by the length of the dataset used as input, so it may not completely sample the atmospheric dynamics of the climate system. The average of resampled analogues is, however, bounded to a lesser extent and can reach values far more extreme than the most extreme ones in the input dataset. The SWG allows the simulation of extreme events outside the observed range but is still limited by the duration of available data.

The length of the factual and counterfactual periods considered was a compromise between the length of the available data (70 years), the non-stationarity of temperatures and the overlapping of the two periods. We needed periods of sufficient length to sample the climate considered correctly. But the shorted overlap between the two periods was necessary to investigate the significance of differences between the factual and counterfactual periods The non-stationarity of climate also means that the longer the periods, the less homogeneous they are in terms of the level of warming. The 50-year periods yield good results in terms of both extremeness (the dataset is large enough to simulate very cold winters) and significant enough difference between the factual and counterfactual periods. Moreover we verified that the analogue days are evenly distributed over the two climate periods and evenly picked during the simulation process. Therefore we consider that the events simulated are representative of the entire analogue period used in the SWG.

This method does not allow us to disentangle anthropogenic warming from other forcings and natural multi-decadal variability in the climate system. But it gives an estimation of the worst-case winter temperature scenario for a given climate period. Another caveat is that the method is mainly based on the use of flow analogues to assess temperatures. It focuses on the link between atmospheric circulation and temperatures and does not take into account other drivers and feedbacks. For instance, snow cover is not considered in the simulations even though it can have a significant impact on extreme winter temperatures (Orsolini et al., 2013).

We showed that a winter as cold as or even colder than the record-breaking event of 1963 could still occur in the current climate at a higher level of warming. This does not mean than such an event will happen in the near future, but it remains possible at the level of warming considered and is relevant from an adaptation point of view. A winter as cold as 1963 would indeed have major impacts on society, especially on the energy system (Añel et al., 2017). For instance, Doss-Gollin et al. (2021) showed that the February 2021 Texas cold snap, which resulted in major failures of the energy system causing energy, food and water shortages, was actually not unprecedented in terms of both temperature anomalies and the resulting heating demand per capita. The lack of preparedness and greater exposure of the energy system due to increasing population and electrification led to disproportionate impacts. In France, the electricity transmission system operator RTE (Réseau de Transport d'Électricité) estimates the sensitivity of electricity consumption to temperature to be 2400 MW °C⁻¹ in winter (RTE, 2021). Hence, it might be desirable for energy systems and logistics to be scaled for the worst-case winter scenarios in the current or future climate conditions and exposures similar to the ones simulated in this study.

The possible occurrence of unprecedented cold winter temperatures in France as simulated in this paper is not inconsistent with the already observed decrease in cold spell intensity in the northern midlatitudes shown by Van Oldenborgh et al. (2019). We focus on very low likelihood winters, with a return period of over 10³ years. This is not representative of meteorological cold waves. For instance, a cold wave in France is defined by Météo France as when the national thermal indicator falls below −2 °C for at least 3 d (Météo France, 2020). A decrease in the intensity of shorter events or an increase in the mean of cold spells is not contradictory to the slow increase in extreme long-lasting winter temperature.

The absence of significant changes in the atmospheric circulation leading to the extreme winters simulated is in line with the typicality of large and persistent temperature anomalies, as shown using large deviation theory (Galfi and Lucarini, 2021; Gálfi et al., 2021). The same atmospheric conditions usually lead to the most extreme events. However these results are valid in a stationary system and obtained using steady-state model simulations. Climate change can lead to important shifts in atmospheric dynamics that could affect the frequency and intensity of extreme events, as well as the dynamics leading to them. The present paper shows no significant shift in the atmospheric circulation of record-breaking winters between the factual and counterfactual periods, which have a difference of 0.72 °C in terms of the level of warming. However these results cannot be extended to a higher shift in global warming level. Simulations of extreme cold spells using the Coupled Model Intercomparison Project phase 6 (CMIP6) simulations (Eyring et al., 2016) would therefore be an extension of this study in order to further explore the evolution of extreme winter temperatures in the midlatitudes in the future – according to different emissions pathways (Riahi et al., 2017) – and the associated atmospheric trajectories.

In this paper, we focused on cold winters (90 d, TG90d) in France. The method can be adapted to simulate cold events of different durations or in other regions. The worst cold spells recorded in France were February 1956 – the coldest month of the 20th century (Andrews, 1956; Dizerens et al., 2017) – and January 1985 (Météo France, 2022a, b). These events caused major disruptions and had a wide health impact (Huynen et al., 2001). The energy sector is sensitive to 15 d events. The cold spell of 3–17 January 1985 is used as the reference event by the French electrical network company. A similar event triggered an unprecedented impulse of solidarity for helping the homeless during winter 1954.

Winter 1963 was the coldest winter recorded in France and a record-shattering event. Using an analogue stochastic weather generator with importance sampling for the simulation of an extremely cold winter, we show that winter 1963 temperatures were already exceptional in the lower level of warming in which it occurred. Estimations of the possibility of such an extreme event occurring in the current climate show that it is still possible to have a winter as cold as in 1963, even if it would remain a highly exceptional event. This paper thus provides a storyline for extremely cold winters in France (Sillmann et al., 2021).

Appendix A: Probability distributions of TGrd according to r

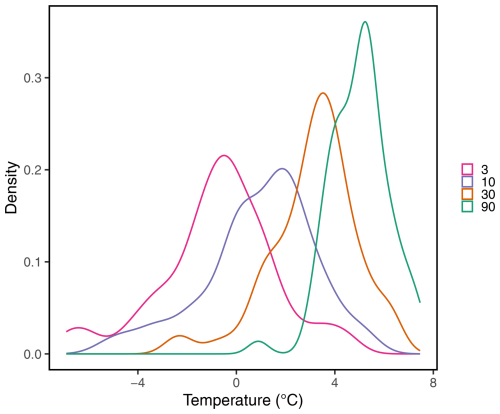
Figure A1 Empirical probability distribution functions of TGrd temperatures with $r\in \mathit{\{}\mathrm{3},\mathrm{10},\mathrm{30},\mathrm{90}\mathit{\}}$ d. The probability density functions are obtained from TG in the ERA5 reanalysis.

We compute the distribution of the annual minima of TGrd for the four r values considered in the paper (3, 10, 30 and 90 d). We obtain empirical probability distributions of TGrd in Fig. A1. As anticipated, the variance of TGrd decreases with increasing r. The probability distribution for r=90 (i.e. the distribution of yearly winter mean temperatures) yields a p value lower than 0.05 when conducting a Shapiro–Wilk normality test, which indicates that it follows a Gaussian distribution. As for the other scales, we compute the minimum of TGrd over a yearly block. The resulting distribution should tend towards a generalized extreme value (GEV) distribution for lower r (Coles, 2001). However, given the non-stationarity of the data and the relatively small sample sizes (n=71), it is challenging to draw any definitive conclusion for lower values of r.

Appendix B: Analogue quality

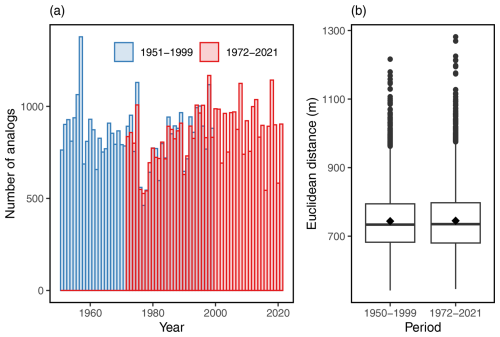
ERA5 data are not stationary because of climate change between 1950 and 2020. This is illustrated for the temperature time series at different event durations in Fig. 1. This also appears in the z₅₀₀ variations due to thermal expansion of the atmosphere. Thus we first checked that the non-stationarity does not affect the distribution and quality of the analogues. Figure B1a shows the year of the 20 best analogues of each winter day of 1950–2021 in either 1951–1999 or 1972–2021. Figure B1b compares the quality of the same two sets of analogues (through the value of the Euclidean distance). We verify that there is no major difference between the two periods and that analogue years show no meaningful trend. Regarding the analogues selected during the SWG simulations, there may indeed be a slight bias towards earlier years in the dataset, but this is not meaningful. The median and mean of the selected analogue years are 1972 and 1973, respectively, for the 1951–1999 period and 1992 and 1994, respectively, for the 1972–2021 period. Therefore, we conclude that the SWG simulations are representative of the climate period of the analogues.

Figure B1 (a) Histograms of years of the K=20 best analogues for each day of the 1951–2021 period in October to March in either 1951–1999 (blue) or 1972–2021 (red). (b) Euclidean distances between z₅₀₀ fields (m) of the analogues in the same two periods.

Appendix C: Climatology of the SWG

The purpose of the α_cal weights is to ensure that the simulations go forward in time and adhere to the seasonal cycle, thereby generating realistic events that do not resemble an eternal-winter scenario with persistently extreme cold temperatures. Yiou and Jézéquel (2020) developed this calendar weighting approach to achieve this objective, and the proportion of days falling at the end of the period of the event is a method that they previously proposed to check if simulated events were deviating from the seasonal cycle. A climatology of the SWG is implicitly computed in Fig. C1 when we initialize the SWG from each 1 December (1951 to 2021) in the ERA5 reanalysis with a calendar constraint but without importance sampling (i.e. α_T=0). Seasonal cycles are not smoothed. The figure shows that the SWG reproduces a seasonal cycle, although the mean seasonal cycle is not as cold as in ERA5. This indicates that the simulated winters yield realistic variations around the seasonal cycle but also that the SWG results are conservative and that colder events may be possible.

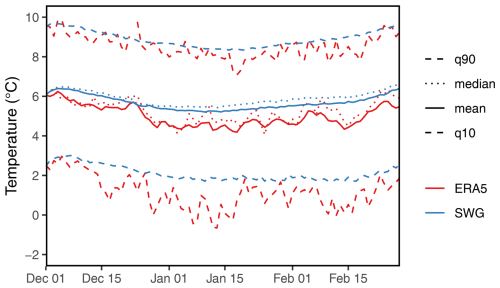
Figure C1 Winter seasonal cycle time series as computed from winters from 1951 to 2021 in ERA5 (red) or from SWG simulations (blue) initialized at the start of the same winters (1000 simulations per winter). The mean (solid lines), the median (dotted lines), and the 10th and 90th percentiles (dashed lines) for both are displayed.

Appendix D: Maps of individual SWG events

Here, we empirically verify that simulations initiated from different conditions yield similar atmospheric patterns. Figure 6 presents the average composite maps of the coldest 10 % of the SWG simulations for each period. Figure D1 demonstrates that these average maps are representative of individual events and that the simulated individual extremes tend to resemble each other. For instance, the z₅₀₀ mean maps of the nine coldest simulations from the SWG using analogues from 1972–2021 are shown.

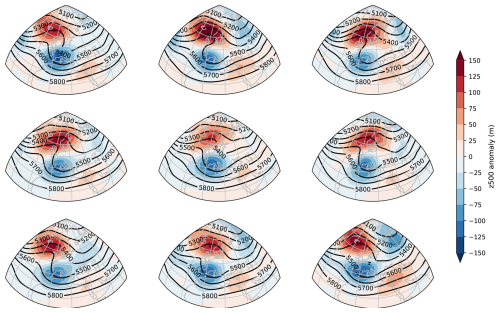
Figure D1 Composites of z₅₀₀ anomalies for the nine coldest individual SWG simulations made from 1972–2021 analogues. The colour scales have a wider range compared to Fig. 6, as they are fitted for individual events.