the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Surrogate-based model parameter optimization in simulations of the West African monsoon
Matthias Fischer
Peter Knippertz
Carsten Proppe
The West African monsoon (WAM) system is a critical climatic phenomenon with significant socio-economic impacts on millions of people. Despite many advancements in numerical weather and climate models, accurately representing the WAM remains a challenge due to its intricate dynamics and inherent uncertainties. Building upon our previous work utilizing the ICON (icosahedral nonhydrostatic) numerical model to construct statistical surrogate models for quantities of interest (QoIs) characterizing the WAM, this paper focuses on the optimization of the three uncertain model parameters of entrainment rate, fall speed of ice, and soil moisture evaporation fraction through innovative multi-objective optimization (MOO) techniques. The problem is approached in two distinct ways: (1) optimization of 15 designated QoIs, such as the latitude and magnitude of the African rain belt or African easterly jet, using existing surrogate models and (2) optimization of twelve 2D meteorological output fields, such as precipitation, cloud cover, and pressure, using new surrogate models that employ principal component analysis. The objectives subject to minimization in the MOO process are defined as the difference between the surrogate model and reference data for each QoI or output field. As reference data, Integrated Multi-satellitE Retrievals for the Global Precipitation Measurement (GPM IMERG) mission are used for precipitation, and the ERA5 reanalysis data from the European Centre for Medium-Range Weather Forecasts are used for all other quantities. The multi-objective optimization problems are tackled through two strategies: (1) assignment of weights with uncertainties to the objectives based on expert opinion and (2) variation in these weights in order to assess their influence on the optimal values of the uncertain model parameters. Results show that the ICON model is already generally well-tuned for the WAM system. However, a lower entrainment parameter would lead to a more accurate simulation of accumulated precipitation, averaged 2 m dew point temperature, and mean sea level pressure over the considered domain (15° W to 15° E, 0 to 25° N). An improvement in 2D output fields instead of QoIs is barely possible with the considered parameters, which confirms meaningful default values of the model parameters for the region. Nevertheless, optimal model parameters strongly depend on the assigned weights for the objectives. To further enhance the accuracy of climate simulations and potentially improve weather predictions, it is crucial to prioritize the refinement of the overall physical models, including the reduction in inherent structural errors, rather than solely adjusting the uncertain parameters in existing model parametrizations. Nevertheless, our methodology demonstrates the potential of integrating statistical and expert-driven approaches to assess and improve the simulation accuracy of the WAM. The findings underscore the importance of considering uncertainties in MOO and the need for a holistic understanding of the WAM's dynamics to enhance prediction skills.
- Article
(5025 KB) - Full-text XML
- BibTeX
- EndNote
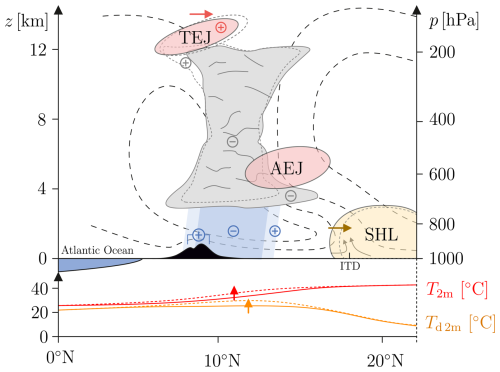
The West African monsoon (WAM) system is characterized by a complex, large-scale circulation pattern, which – mainly through its control of rainfall – has substantial socio-economic impacts (Haile, 2005). An accurate simulation of the WAM in numerical weather and climate models continues to be a considerable challenge, primarily due to the inherent uncertainties and multi-scale, nonlinear interactions within the system. The WAM originates from the complex interplay between the Atlantic Ocean, the vast Sahara Desert, and the African rainforests (Hastenrath, 1991; Hall and Peyrillé, 2006). During boreal summer, intense solar heating over the Sahara creates a low-pressure area, drawing moist air from the cooler Atlantic Ocean inland. This influx of moisture-laden air leads to the formation of a rain belt, which brings significant rainfall to the Sudano-Sahelian region. In addition to the rain belt, key features of the WAM include the intertropical discontinuity (ITD); an air mass boundary where the northeasterly Harmattan and southwesterly monsoon winds converge, and the African easterly jet (AEJ); a mid-tropospheric easterly wind maximum that influences the development and movement of weather systems across the region (Nicholson, 2009; Thorncroft et al., 2011; Fink et al., 2017). The tropical easterly jet (TEJ) at higher altitudes and the Saharan heat low (SHL) are also critical components of the system, affecting atmospheric circulation and precipitation patterns (Flohn, 1964; Lavaysse et al., 2009). The intricate relationship between these dynamics and various atmospheric processes such as deep convection and cloud formation significantly influence the WAM's precipitation distribution and intensity (Mathon et al., 2002; Lebel et al., 2003; Lebel and Ali, 2009; Kendon et al., 2019; Tchotchou and Kamga, 2009). Furthermore, diabatic processes directly affect the realism of simulations of rainfall and the overall WAM circulation (Marsham et al., 2013; Martin et al., 2017). Challenges in modeling these processes, alongside the need for improved grid resolution and parameter choices, have been widely recognized as primary sources of uncertainty in WAM simulations (Cook and Vizy, 2006; Xue et al., 2010; Vellinga et al., 2013). Furthermore, the onset, intensity, and withdrawal of the WAM are influenced by factors such as sea surface temperatures (Messager et al., 2004) and vegetation (Zheng and Eltahir, 1998).
In order to better understand the sensitivity of the WAM to parameter choices in atmospheric models, our prior study (Fischer et al., 2024) utilized the ICON (icosahedral nonhydrostatic) model (Zängl et al., 2015) to simulate the WAM over a nested limited-area domain (28° W to 34° E, 10° S to 34° N) and used the model output to construct surrogate models by means of universal kriging (Rasmussen and Williams, 2005). In that study we varied six uncertain ICON model parameters from the ensemble perturbation namelist (Deutscher Wetterdienst (DWD), 2019), but our analysis revealed that only three of those, namely the entrainment rate (entrorg), the terminal fall speed of ice crystals (zvz0i), and the soil moisture evaporation fraction (c_soil), exert substantial influence on the WAM system. The impacts of varying entrorg and zvz0i were particularly pronounced, affecting designated quantities of interest (QoIs), which characterize the WAM system, such as the position and strength of the AEJ and the SHL. Enhanced entrorg was associated with a general drying effect on the WAM system, leading to decreased precipitation, reduced high-level cloud cover, and a general southward shift of several WAM features. Interestingly, increasing entrorg also resulted in a localized precipitation increase along the central axis of the rain belt, suggesting a concentration of rainfall in areas with favorable ambient conditions. The challenge of tuning the entrainment rate, particularly in the tropics, has often been highlighted. For instance, low entrainment rates have been associated with higher climate sensitivities due to enhanced deep convection and increased moisture transport into the upper troposphere, potentially leading to an unrealistic cloud effect (Stainforth et al., 2005; Sanderson et al., 2008; Sexton et al., 2011). Additionally, Zhu and Hendon (2015) showed that an increased entrainment can improve Madden–Julian oscillation simulations by modulating convection, although the model may still fail to capture the essential moistening by shallow convection. Changes in zvz0i resulted in similar effects but with some differences in the spatial distributions and magnitudes, particularly regarding high- and mid-level cloud cover. The parameter c_soil showed a distinct influence through altered surface evaporation. Higher values lead to higher dew points and lower temperatures over land. The increase in surface moisture contributes to changes in precipitation and cloud cover, particularly at low levels.
Numerical weather prediction (NWP) models, such as the ICON model, involve a substantial number of parameters that must be carefully tuned. While some parameters represent physical quantities (e.g., fall speed of ice), others are non-physical constants in parametrization schemes that cannot be directly measured (e.g., soil moisture evaporation fraction) but are essential for representing sub-grid-scale processes. Highlighting the complexity, Zängl (2023) noted that many parameters within the ICON model have a range of values with no clear optimum. Modifying a parameter may improve model performance in some regions or seasons while degrading it in others or may enhance certain forecast variables at the expense of others. Traditionally, parameter tuning has been conducted by experts without a unified framework. History matching (Williamson et al., 2013) has emerged as a prominent technique for quantifying parameter uncertainties by systematically exploring a range of plausible model configurations and eliminating parameter sets that fail to reproduce observations within acceptable tolerances. This approach is particularly useful in the tuning of climate model parameters, such as those governing aerosol–cloud interactions, where direct measurements are often challenging to obtain (e.g., Lee et al., 2016). Over the past decades, automatic calibration techniques have emerged, incorporating data assimilation methods into operational weather forecasts. A comprehensive review by Ruiz et al. (2013) focused on these techniques, and Zängl (2023) described the current implementation in the ICON model. Ruiz et al. (2013) emphasized that objective optimization often becomes infeasible when complex numerical models and a large number of parameters are involved. To address this, surrogate-based optimization techniques have gained attention in meteorological studies. These methods replace the expensive numerical models with cheaper surrogates, often referred to as meta-models or emulators, which can be trained with fewer NWP evaluations. For example, quadratic meta-models were used to approximate climatic variables by Neelin et al. (2010) and Bellprat et al. (2012). Similarly, Ray et al. (2015) employed a Gaussian process and polynomial regression for the Bayesian calibration of the Community Land Model. Chang et al. (2014) utilized principal component analysis in conjunction with Gaussian process regression to develop surrogate models for calibrating the Greenland Ice Sheet model. In another study, Lu et al. (2018) applied advanced sparse grid interpolation as a surrogate model for the E3SM Land Model, using quantum-behaved particle swarm optimization to identify optimal parameters. Various software packages have also been developed to facilitate specific optimization procedures, such as the toolkit by Watson-Parris et al. (2021), which supports model calibration using a range of surrogate models (e.g., Gaussian process regression), and the parameterization improvement tool by Couvreux et al. (2021), which incorporates Gaussian process regression, history matching, and other techniques.
Despite these advancements, defining suitable objectives remains challenging due to the diverse range of meteorological variables involved. Multi-objective optimization (MOO) studies have emerged to combine multiple variables, where compromises are identified via Pareto fronts. On such Pareto fronts, an improvement in one objective necessitates the deterioration of at least one other objective. Surrogate-based optimization has proven particularly effective for these complex MOO problems, which often require high computational effort. Several studies have focused on identifying Pareto fronts using surrogate models (Shafii and De Smedt, 2009; Gong et al., 2016). Other studies have simplified the analysis by predefining the weighting of objectives, thereby reducing the problem to a single-objective optimization problem. For example, Cinquegrana et al. (2023) assigned equal weights to all objectives. Instead of combining meteorological variables independently in the MOO process, different criteria might be employed, such as the energy norm used by Ollinaho et al. (2014). However, due to the limited number of variables recorded in our study because of data storage constraints, we focus on these variables for optimizing the model parameters. As Zängl (2023) argued, trying to select optimal parameters inherently involves subjective decisions, e.g., prioritizing certain forecast variables or regions. Furthermore, there is a risk that calibrated model processes might compensate for model errors originating from different parametrizations.
To conduct parameter optimization studies, we employ surrogate models to describe the relationship between ICON model parameters and QoIs or full 2D output fields. For the QoIs, we utilize the surrogate models from Fischer et al. (2024). For the 2D output fields, we develop new surrogate models using principal component analysis (PCA) combined with a regression model. We focus our study on the most impactful model parameters, namely entrorg, zvz0i, and c_soil, as global sensitivity analysis (GSA) and validation tests have revealed that the other three model parameters discussed in Fischer et al. (2024) only exert a little influence on QoIs and output fields. The objectives for minimization are defined as the differences between the surrogate model and reference data for each respective QoI or output field. As reference data, we utilize the Global Precipitation Measurement (GPM) of the Integrated Multi-satellitE Retrievals (IMERG) (Huffman et al., 2019) for precipitation and ERA5 reanalysis data provided by the European Centre for Medium-Range Weather Forecasts (ECMWF) (Hersbach et al., 2020) for all other atmospheric variables. Parameter optimization in meteorological modeling has often not focused on the simultaneous consideration of multiple model outputs, and no general framework has been established for this purpose. In this study, we present a novel approach for determining optimal model parameters by incorporating uncertainties in the predefined weights of quantities of interest (QoIs) and output fields and by systematically examining the effects of varying these weights. To the authors' knowledge, no previous meteorological studies have explored the impact of weight variations in MOO in this manner. Also, no studies have conducted such an extensive exploration of model parameter calibration specifically for the West African monsoon system. Our approach, integrating both statistical and expert-driven perspectives, offers a promising pathway to improve simulations of the WAM system and to broaden our understanding of it.
The paper is organized as follows: Sect. 2 outlines the methods employed in this study, including the optimization strategies, as well as the employed data. Section 3 presents the results, focusing on the outcomes of the optimization process and their implications for WAM simulations. Finally, Sect. 4 offers a summary and conclusions of our findings, along with a brief outlook on future research directions in this field.
In this section, we briefly introduce the setup of the ICON model, outline the reference data, and demonstrate the computation of objectives subject to minimization, including the surrogate models developed for this purpose. Finally, we explain the MOO process.
2.1 ICON model
The ICON model (Zängl et al., 2015), the operational forecast system of the DWD (German Meteorological Service), is used here as the full-physics numerical model to simulate the WAM. For this purpose, we employ the 2.5.0 model version in a limited-area nested configuration, where a 26 km grid spacing for the outer region and a 13 km grid spacing for the inner region are used. The outer area extends from 28° W to 34° E and from 10° S to 34° N with the nested domain 2° smaller in each direction. At the outer boundary, ERA5 reanalysis data are used. ERA5 data are available hourly but are updated every 6 h in our simulations to limit the amount of data and computation cost. Apart from this, the model setup, including all namelist parameters, is based on the configuration used in the operational global setup by the DWD. Pante and Knippertz (2019) already obtained reasonable simulation results for the West African region with a similar model setup, although the convection parametrization turned out to be problematic for precipitation forecasting. ICON simulations are initialized on 21 July in the years 2016 to 2019 and run for 41 d. Simulation output data are stored with a horizontal resolution of 0.1° within the region from 0 to 25° N and 15° W to 15° E and a temporal resolution of 1 or 3 h (depending on the variable) from 1 to 31 August of the years 2016 to 2019. All 2D output fields are averaged over the whole time period. The output fields and the QoIs computed from these fields, which represent key characteristics of the WAM, are listed in Table 1. The experimental design consists of 60 training points xi(i=1…60), i.e., combinations of the six considered ICON model parameters. These parameters were chosen based on expert judgment, as they were expected to have a substantial impact on WAM quantities. For each training point i, the QoIs yij(i=1…60) were computed based on the temporally averaged 2D output fields. Surrogate models were developed using Gaussian process regression to describe a relationship between the six model parameters and each QoI j. Our previous study demonstrated that only the three parameters of entrainment rate (entrorg), terminal fall speed of ice crystals (zvz0i), and soil moisture evaporation fraction (c_soil) had a substantial impact on the monsoon system. More details on the model setup and uncertainty contributions are given in Fischer et al. (2024). Consequently, the optimization process in this study is limited to variations in these three parameters to minimize the risk of overfitting, as including parameters with low sensitivity would not produce meaningful adjustments. In hindsight, building surrogate models based solely on an experimental design that perturbed these three parameters would have been advantageous. That approach would likely yield higher model accuracy by concentrating the same number of training points in a lower-dimensional input space. However, since the simulation results had already been obtained in our prior study at considerable computational expense, we opted to use the existing data for the optimization studies to avoid further computational costs. The surrogate models are validated within the 6D input space and are thus considered valid within the 3D subspace for this study. Parameters not included in the optimization process are kept at their default ICON model values.
2.2 Reference data
Selecting appropriate reference data is crucial for identifying optimal model parameters. In our study, we utilize GPM IMERG data for precipitation due to its high-resolution and extensive coverage, crucial for accurately capturing the spatial and temporal variability in rainfall within the WAM region. For other atmospheric variables, such as temperature, pressure, and wind patterns, we rely on the ERA5 reanalysis data. For the optimization using 2D field data, the ICON model output (horizontal resolution of 0.1°), native ERA5 data (horizontal resolution of 0.25°), and native GPM IMERG data (horizontal resolution of 0.1°) are linearly remapped on a rectangular grid with a mesh size of 0.5° and averaged over the August months of 2016–2019. The spatial resolution is chosen as a compromise between accuracy and computation time for the MOO process. The reference values for the QoIs from the reference data are determined by the same procedure as for the ICON model outputs.
2.3 Objectives
The objectives for the individual QoIs and full 2D output fields are defined such that a minimization in the optimization process would lead to the desired improvement of these quantities through the identified modification of the three considered model parameters, namely the entrainment rate, the terminal fall speed of ice crystals, and the soil moisture evaporation fraction. The two approaches incorporate the QoIs and output fields listed in Table 1.
-
Quantities of interest (QoIs). Here, our goal is to improve the accuracy of variables related to the WAM. To achieve this, we employ surrogate models developed in Fischer et al. (2024) for the 15 designated QoIs that are listed in Table 1. The individual objectives are formulated as the squared error between the QoI from the surrogate model ℳQoI,j and from the reference data yref,j. The j=1…15 objectives for the individual QoIs subject to minimization are
where is the vector of the three model parameters. In the surrogate models, the other three parameters, which are not investigated here, are set to their default values.
-
Full 2D output fields. For the optimization of full 2D output fields, we employ the averaged 2D output fields for the 60 training points xi(i=1…60) from Fischer et al. (2024). The results in Fischer et al. (2024, their Figs. 7–9) provide insight into the individual influence of model parameters on the output fields. However, these results only consider the difference between output fields for the 25 % lowest and 25 % highest values of the model parameters among all training points, neglecting interactions between multiple parameters. Using the 25 % training points from each side was considered a compromise between significance (utilizing enough training points for the average) and separation (only using training points for very high and very low parameter values) and assuming a fairly monotonic relationship between parameters and output fields. Furthermore, GSA revealed little interaction between the parameters. In this study, however, for a more sophisticated optimization strategy, surrogate models for the full 2D output fields are determined and used in the optimization process. Principal component regression is employed as a surrogate modeling technique for approximating 2D fields due to its effectiveness and interpretability. In contrast, neural-network-based approaches, such as autoencoders, typically require substantially larger datasets, which are not feasible in this case due to the high computational cost of running ICON model simulations to generate training data.
The temporally averaged 2D fields of the meteorological variables j=1…12 for the n=60 training points xi(i=1…n) are given by with 50 latitudinal and 60 longitudinal grid points. These data are standardized using the mean,
and the standard deviation,
of all n training points at each grid point (k,l) and for each variable j. The grid point data of the standardized field plots can then be expressed as
with zero mean and unit standard deviation at each grid point (k,l) for each variable j.
PCA is performed separately on each variable j using the data . For this purpose, the matrix components of are reshaped into vectors. The covariance matrix is then computed for each variable j using all data points i=1…60. The eigenvectors of this covariance matrix are computed and transformed back into matrix form, resulting in the principal fields Pmj (m=1…P), with P principal fields for each variable j. These fields represent the major variations within the field data for each variable j. Each field Mj of meteorological variable j can now be approximated as a linear combination of the principal fields with respect to input parameter vector x:
In our study P=3 principal fields lead to a high accuracy and are considered to be a good compromise between accuracy and computation time. For the coefficients, we use a linear trend with respect to the physical model parameters. Since we use the vector x in an independent and identically distributed (i.i.d.) uniform input space, we incorporate the transformation of the input space in the definition of ansatz functions using the inverse cumulative distribution function CDF−1. This transformation corresponds to the input space transformation described in Fischer and Proppe (2023), where more detail is given on the transformation process. The ansatz can then be formulated as
with respect to the i.i.d. uniform input parameters . The coefficients are then determined by minimizing the mean squared error between the surrogate model and the training data for each variable j separately:
Traditionally, when a linear model is used for the coefficients with respect to the parameters, an analytical solution for the coefficients can be derived directly from the minimization process, often linking them to the PCA eigenvalues and their associated energy content (Jolliffe, 1986). In contrast, the nonlinear nature of the ansatz functions introduced by the input space transformation in our approach necessitates a numerical optimization of . The input space transformation serves to improve model accuracy by addressing distortions in the parameter space, ensuring a better fit of the surrogate model to the data. Although this approach may alter the conventional interpretation of the coefficients with respect to the principal modes' energy content, it remains a valid and practical method for enhancing surrogate modeling performance. Further methodological details and implications are discussed in our previous work (Fischer and Proppe, 2023). Then, we define the objectives as the sum of mean squared errors between Mj(x) and reference data Yj,ref over all 50×60 grid points. The j=1…12 objectives for the individual meteorological variables j are
As before, for optimization purposes, only the three model parameters considered in this study are optimized, while the remaining three parameters are maintained at their default values. Figure 2 shows the field plots Mj,mean for the ICON mean data, the reference data Yj,ref, and the difference between the two () for each output variable j. The optimization target is to identify the model parameters x, where the difference between predicted ICON field Mj(x) and reference field Yj,ref becomes minimal.
2.3.1 Model validation
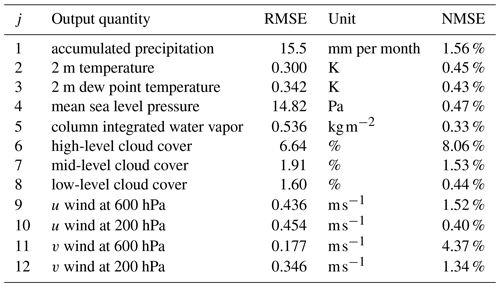
Surrogate models representing the complete 2D output fields must be validated to ascertain their precision. The validation of the surrogate models for QoIs has been conducted in our previous study (Fischer et al., 2024). The accuracy of these 2D surrogates depends on several factors, including the number of training points, the chosen modeling methodology (e.g., PCA, the number of principal fields, the ansatz for the coefficients), and the presence of nonlinearities or chaotic behavior within the physical model. Similar to the validation process for QoI surrogate models, validation of the 2D surrogates is conducted using the root mean squared error (RMSE) and the normalized mean squared error (NMSE) for variable j, employing leave-k-out cross-validation:
Here, denotes the variance of the field data for variable j across all grid points (k,l) and represents the surrogate model for variable j derived from all n training points except those within set K(i) containing the ith point. We employ leave-k-out cross-validation with k=2 to balance validation accuracy and computational efficiency, necessitating the repetition of the entire training process, including PCA, for each model . Consequently, the sets are defined as , e.g., .
It is crucial to utilize generalization errors rather than goodness-of-fit measures like the coefficient of determination R2 to account for overfitting. While RMSE provides insights into absolute error values, NMSE offers a dimensionless measure facilitating a better comparison between the variables. Model accuracy is deemed high if NMSE values approach 0 and low if they approach 1. These values are inherently non-negative and should not exceed 1, as exceeding this threshold would indicate that the covariance between the surrogate model and the data surpasses the data's variance.
2.4 Multi-objective optimization
In this study, our aim is to solve a MOO problem with 3 model parameters and 15 (QoIs) or 12 (output fields) objectives. Given the complexity in such a high-dimensional objective landscape, identifying Pareto fronts is considered impractical due to the extensive computational resources required and the challenges in interpreting the results. Consequently, we simplify this MOO problem by reducing it to several single-objective optimization problems. The reduced objectives are defined based on a combination of the components of the original MOO problem. By employing a weighted sum, we assign a relative importance to the individual objectives.
The total reduced objective functions using the QoIs and the 2D output fields are then
where wQoI,j and woutput,j are weights for the individual objectives that have to be specified in advance. To ensure the weighting of the variables is meaningful and significant, the meteorological variables are normalized with respect to their variation. For this purpose, the standard deviations σQoI,j of evaluations yij(i=1…60) and σoutput,j of 2D field data are used. It should be noted that other normalization methods are conceivable, which could, in turn, influence the weighting. This further highlights the issue with selecting fixed weights, thus motivating an investigation into the impact of different weights in this study.
The variation in model parameters should be confined to plausible values. Fischer et al. (2024) used probability density functions (PDFs) constructed based on expert assessments and previous parameter identification studies. These PDFs for the three considered model parameters are depicted in light grey in Fig. 4. The boundaries of the model parameters in the optimization process are set at the 1 % and 99 % levels of the cumulative distribution function. These boundaries are considered appropriate to maintain the physical plausibility of the values and to account for the reduced accuracy of surrogate models at the distribution tails.
However, a certain set of weights would not allow for a comprehensive understanding of the optimal parameters because the parameters may be highly sensitive to the choice of weights. Therefore, it remains inevitable to consider variation in the selected weights. We approach this in two ways: (1) by inducing uncertainty to the weights to investigate the sensitivity (spread) in the optimal parameters and (2) by varying the individual weights separately to investigate the isolated influence.
Table 1Weights of the objectives used for the weight uncertainty method in MOO for both output fields and QoIs.
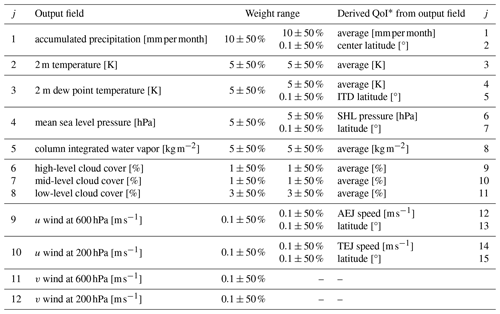
* See Fischer et al. (2024) for details. “Average” corresponds to the spatial average over the whole domain (15° W to 15° E, 0 to 25° N).
-
Weight uncertainty. To incorporate the sensitivity of optimal parameters to variations in the weights of the objectives, we introduce uncertainty in these weights, using expert judgment to define their relative magnitudes. Specifically, we apply the weights along with uniform uncertainty intervals, as indicated in Table 1. It is important to note that the choice of uniformity lacks a physical foundation; the intervals are primarily introduced to induce uncertainty. While other distributions or probability concepts (e.g., probability boxes) could be applied, we limit our choice to uniform distributions for the sake of interpretability and simplicity. Precipitation is assigned the highest importance due to its pivotal role in the WAM system and for user applications. Secondary importance is assigned to temperature, dew point temperature, pressure, and column integrated water vapor, all considered essential but subordinate to precipitation. Cloud cover is attributed a lesser significance, with emphasis on low-level clouds. Wind speeds are assigned the smallest weights. In this multidimensional weight space, we conduct Monte Carlo simulation with 1000 samples, where each sample represents one reduced single-objective optimization problem with a certain combination of weights. The outcomes of this simulation are presented as histograms for the optimal model parameters.
-
Weight variation. Compared to the previous method, the aim of the weight variation approach is not to find an averaged optimum of the conflicting objectives but to investigate the dependence of the optimal parameters on the weights of the objectives. For this purpose, we consider the weight (relative importance) of one objective which is varied step-wise between 0 % and 100 %. The weights of all other objectives are defined relative to each other based on their mean values according to Table 1 such that the sum of all weights is 100 %. To strike a balance between the integrity of the results and computational efficiency, a total of 15 incremental steps were employed for the weight adjustment for each objective.
Several software packages for parameter calibration have been developed in recent years (e.g., Watson-Parris et al., 2021; Couvreux et al., 2021), and these tools are generally applicable across various contexts. However, given the specific requirements of this study – such as input space transformations, the use of ansatz functions for universal kriging, and variations in objective function weights – this work employs a combination of widely adopted Python packages, which have been adapted to meet the study’s goals. Optimization tasks were performed using the “SciPy” package for Python, specifically utilizing the Nelder–Mead method (Virtanen et al., 2020).
The initial step involves validating surrogate models for the 2D output fields and comparing the simulation outputs using ICON default parameters with reference data. Evaluating the physical or technical discrepancies inherent in the field data is crucial for refining model parameters, as it may reveal limitations within the optimization framework. Based on this foundation, the optimization results are then presented and discussed, first based on QoIs and then on the full 2D output fields.
3.1 Model validation
Validation offers critical insights into the significance and reliability of the results. Leave-k-out cross-validation (k=2) was conducted for the surrogate models representing the entire 2D output fields, as outlined in Sect. 2.3. Table 2 shows both the RMSEs and NMSEs for all variables. These metrics comprise both the inherent aleatoric uncertainties stemming from the chaotic nature of weather simulations and the uncertainties arising from the surrogate models. It is important to acknowledge that large errors do not necessarily indicate surrogate models with low accuracy, as they might also indicate substantial aleatoric uncertainties in respective quantities. Furthermore, due to regional variability, the comparison of grid point data within the validation procedure inherently leads to substantially larger errors compared to domain average comparisons for the validation of QoIs (Fischer et al., 2024, Table 3). In our analysis, small NMSEs are evident across all variables except for high-level cloud cover (NMSE 8.06 %) and v winds at 600 hPa (NMSE 4.37 %). Considering these variables have relatively low weights in the optimization process (see Table 1) and that for v winds at 600 hPa the RMSE is also relatively low (0.177 m s−1), large NMSE values in these variables are not considered to impact the overall validity of this study.
3.2 Comparison of ICON output to the reference data
Before analyzing the optimization results, it is crucial to examine notable discrepancies between the ICON model output and the reference data GPM IMERG and ERA5 to illustrate constraints and prospects for the optimization process. Figure 1 illustrates the ICON mean ℳQoI,j(xmean) and reference data yref,j for each QoI j (right panels) together with the results from the surrogate models from Fischer et al. (2024). Figure 2 shows the ICON mean field Mj,mean, the reference field Yj,ref, and the difference between the two () for each variable j.
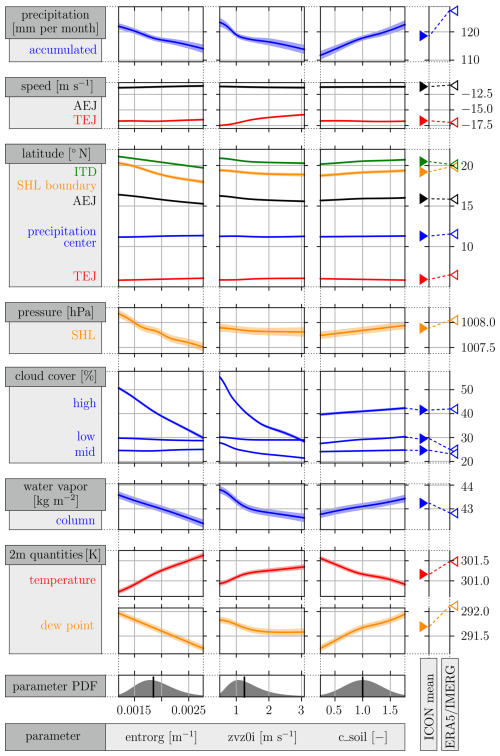
Figure 1Dependencies of all QoIs (ordinate) with respect to the three uncertain model parameters (abscissa). Shaded area around curves illustrates prediction variance from the Gaussian process regression model. In each plot, only one model parameter is varied, while all other model parameters are set to their mean value. Model parameter PDFs including their mean value are shown at the bottom (Fischer et al., 2024). Panels on the right side show the QoI values from ICON simulations using default model parameters and from the reference data (ERA5 reanalysis data and GPM IMERG for precipitation).
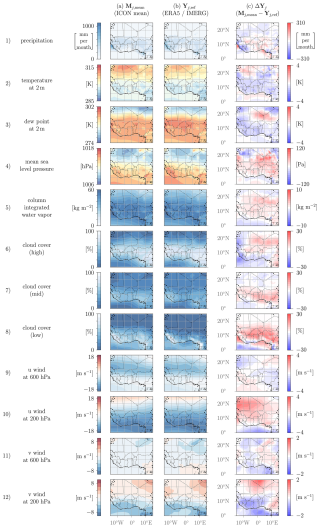
Figure 2Averaged output fields from ICON simulations using default model parameters, from reference data (ERA5 reanalysis data and GPM IMERG for precipitation), and the difference of ICON minus reference.
There is an overall reasonable agreement in most fields between ICON simulations and the ERA5 and GPM IMERG references. In the following discussion we will focus on the most critical variables according to the assigned weights (Table 1).
With respect to precipitation, the domain mean rainfall from ICON simulations is approximately 10 % lower than that observed in GPM IMERG data (Fig. 1, first row). ICON underestimates rainfall in coastal (southwestern West Africa, Niger Delta) and mountainous regions (Guinea Highlands, Cameroon line) and over the Sahara with a slight overestimation in central West Africa (Fig. 2(1c)), whereas the precipitation center remains almost unchanged (Fig. 1, seventh line from top). This is despite the findings in Kniffka et al. (2019), where models using parameterized convection, as is the case in our study, tend to inaccurately capture the northward migration of the rain belt, resulting in reduced rainfall in the Sahel. The former observation indicates that the model has difficulties in capturing rain enhancement by topographic features. A follow-on study by Kniffka et al. (2020) showed that the total rainfall from ICON simulations with parameterized convection largely agrees with station data in southern West Africa, whereas IMERG data exhibit a negative bias relative to the stations, which demonstrates some uncertainty in the observational reference. Overall these results leave it open, whether changes to model parameters can cure the rainfall deficiencies or whether this mostly requires a better representation of topography.
The dominating pattern in the mean sea level pressure (MSLP) differences is a zonal dipole with slightly higher pressure in ICON in the east and lower pressure in the northwest of the domain compared to ERA5 (Fig. 2(4c)), leading to a deeper SHL in ICON (Fig. 1). The pressure pattern is strongly correlated with 2 m temperatures, where higher pressure values correspond to lower surface temperature values (Fig. 2(2c)). At the same time 2 m dew point is reduced in ICON apart from an area around the Algeria–Mali–Niger border triple point (Fig. 2(3c)) but with little impact on the mean ITD latitude (Fig. 1). Despite this, ICON has higher column integrated water vapor in most parts of West Africa (Fig. 2(5c)) and on average (Fig. 1), indicating differences in the vertical distribution of water vapor between ICON and ERA5.
This is to some extent reflected in cloud cover differences at low, mid, and high levels. With respect to low-level cloud cover, ICON simulations show a pronounced positive bias over almost the entire rain belt area relative to ERA5 reanalysis, with a minor negative bias over the equatorial Atlantic Ocean (Fig. 2(8c)). This implies a northward extension of the low-level cloud belt in ICON (Fig. 2(8a)). The averaged low-level cloud cover in ICON reaches 30 % and thus significantly exceeds that of ERA5 data of 25 % (Fig. 1). Such a large difference is somewhat surprising, as it is mostly accompanied by a lower 2 m dew point temperature corresponding to a lower absolute humidity (not shown). This indicates that a calibration with the chosen uncertain model parameters will not be straightforward and could only be achieved through complex interactions within the WAM system. Representing low-level cloud cover has been identified as a significant challenge in prior research, with a notable discrepancy between various models and observational data (Hannak et al., 2017; Kniffka et al., 2020). Notably, Kniffka et al. (2020) showed that low-level cloud cover in ICON utilizing parameterized convection deviates by only 2 % from station data, casting some doubt on the quality of the ERA5 cloud estimates. Mid-level clouds are also mostly enhanced in ICON over the rain belt area but weakened elsewhere (Fig. 2(7c)). High-level clouds in contrast are mostly less widespread in ICON with the exception of areas in Mali and Niger (Fig. 2(6c)). This disagrees somewhat with Kniffka et al. (2019), where an overestimation of high-level clouds in ICON was found.
There are also some moderate differences with respect to circulation. The TEJ is weaker and shifted southward, whereas the characteristics of the AEJ remain relatively unchanged (Fig. 1). The horizontal distributions of differences between ERA5 and ICON show that the subtropical jet is also shifted southward in ICON (Fig. 2(10a, b, c)), while differences in zonal wind at 600 hPa are rather small (Fig. 2(9c)). Finally, fields in meridional wind show only moderate differences with a fairly patchy pattern both at 600 and 200 hPa (Figs. 2(11c) and (12c)).
For a better overview, Fig. 3 summarizes the desired changes in WAM characteristics in model simulations if the reference data are targeted. Precipitation should generally increase but mainly in the mountainous regions close to the Atlantic coast. The SHL should weaken and move northward. Cloud cover should decrease at low and mid levels, while an increase at high levels to the south of the rain belt is desired. The 2 m temperature and 2 m dew point temperature should increase on average over southern West Africa. The TEJ should be slightly enhanced, while the AEJ should remain unaffected.
3.3 Optimization based on quantities of interest
In the following, we will present the results of the optimization with respect to the 15 QoIs. Figure 4 shows histograms of the three optimized model parameters using the weight uncertainty method from Sect. 2.4. Each data point corresponds to the result of an individual single-objective optimization with different weights. For reference, the parameter PDFs employed in Fischer et al. (2024) are depicted in light grey. For entrorg the histogram collapses into optimal values very close to the lower boundary defined in the optimization process. This result demonstrates that the optimization is strongly controlled by the attempt to enhance rainfall in ICON to better match the wetter GPM IMERG data. The most effective way of doing this is by reducing entrainment rates, pushing the optimal values almost to the lowest plausible level. Given that we suspect an influence of topographic rainfall enhancement (see Sect. 3.2), this may lead to a better agreement but not necessarily a physically more realistic model configuration. This underscores the challenge of tuning the entrainment rate in tropical regions. The other two parameters, zvz0i and c_soil, tend to converge towards values close to the means of their original PDFs, with zvz0i narrowly clustered slightly above its mean () and c_soil more broadly distributed slightly below its mean (∼0.8). This suggests that the default settings for these two parameters already provide a relatively good balance for the considered system. The histograms' pronounced peaks for entrorg and zvz0i imply a relative insensitivity to weight variations. This is also supported by the GSA in Fischer et al. (2024), where most QoIs turned out to be very sensitive to these two parameters such that only small changes would substantially affect most QoIs.
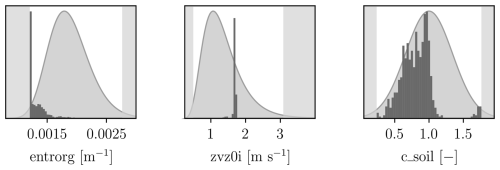
Figure 4Histograms of optimal model parameters as a result of Monte Carlo simulations with weights from Table 1 for optimizing QoIs.
Figure 5 shows histograms of the optimized QoIs corresponding to the parameters in Fig. 4. Vertical lines indicate the values from ICON simulations using default model parameters (solid) and reference data (dashed), corresponding to the right panels in Fig. 1. Generally, QoIs with larger weights (Table 1) shift more markedly from their default towards the reference values. The strong weight for precipitation yields a ∼ 30 % improvement relative to GPM IMERG data. Similarly, 2 m dew point temperature and MSLP show significant improvements with regard to ERA5 data, owing to their medium weights. Conversely, column integrated water vapor and 2 m temperature deteriorate, highlighting an inevitable trade-off in MOO for an overall optimum. The effects on these QoIs become clear, since only the entrainment rate is substantially changed and a decrease in this parameter leads to increased precipitation, reduced 2 m temperature, a higher 2 m dew point, a weaker SHL, and more column integrated water vapor (see Fig. 1). With regard to cloud cover, only mid-level cloud cover shows a strong improvement due to the slightly increased fall velocity of ice (Fig. 1), while low- and high-level cloud cover shows no improvement mostly due to the lower weighting. As discussed in Sect. 3.2, accurately capturing low-level cloud cover remains a challenge for both models and measurements, with none of the considered model parameters or their combinations being able to create a satisfactory solution. This also becomes clear from Fig. 1, where for certain QoIs, such as low-level cloud cover, no parameter combination would lead to alignment with the reference data. Furthermore, QoIs with even lower weights can experience rather diverse changes through the optimization, including deterioration with regard to the reference values (e.g., ITD latitude, AEJ and TEJ speeds and latitudes). This phenomenon illustrates that enhancing certain QoIs often compromises others, indicative of results situated on Pareto fronts. The inability to simultaneously optimize all QoIs to match reference data suggests potential physical discrepancies in the reference datasets or in the ICON model. The marked degradation of certain low-weighted QoIs also highlights the potential risk of overfitting to highly weighted QoIs.
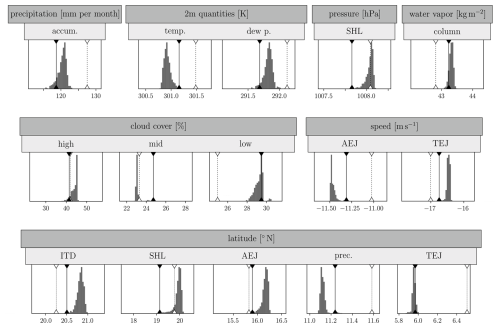
Figure 6 shows the optimal model parameters for varied weights, where each data point represents a single-objective optimization problem. The optimal parameters generally align with those in Fig. 4. However, substantial impacts on optimal parameters are observed for several QoIs when weights vary. In certain instances, although the overall trends are pronounced, minor oscillations or jumps may be observed. These fluctuations are likely attributable to factors inherent in the optimization procedure, such as tolerances and numerical considerations, but could also indicate the presence of multiple local minima. Due to the complex approach, which includes many separate optimization runs, a global optimization procedure is considered infeasible because of the computational effort required. Nonetheless, these variations do not compromise the significance of the results, given the clarity of the predominant trends. For high-weighted low-level cloud cover, significant parameter adjustments are found, i.e., a large entrainment rate and fall velocity of ice. This aligns with the much lower reference values of low-level clouds shown in Fig. 1. However, despite these adjustments, the achievable values for low-level cloud cover remain far from the reference values. As explained in Sect. 3.2, it remains problematic to enforce an optimum in this quantity. For higher weights on the QoIs' 2 m dew point temperature and accumulated precipitation, higher c_soil values are favored, as increased surface latent heat fluxes consistently lead to higher dew points. These findings are supported by Fig. 1, as the surrogate values for these QoIs approach the reference values with higher c_soil values. With regard to the considered latitudes, the entrainment parameter shows the strongest impact (see Fig. 1). High weights on the latitudinal position of WAM features generally lead to a larger optimal entrainment rate. This increased entrainment rate compresses the latitudinal extent of the WAM system, making it narrower, which better matches the ERA5 reanalysis data.
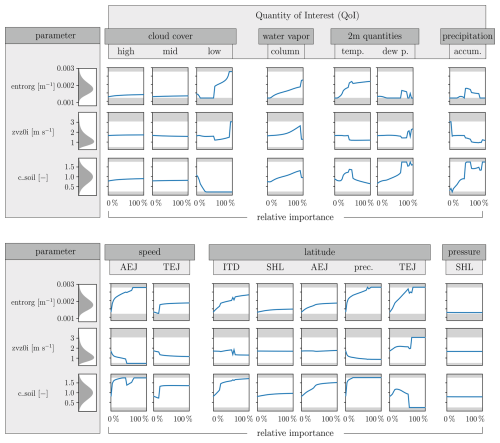
Figure 6Optimal model parameters resulting from MOO. Weights (relative importance) for individual QoIs are successively increased, while weights for all other QoIs are specified based on their mean values in Table 1, summing to 100 %. A separate optimization problem is solved for each weight combination.
The rather unpredictable changes in the parameter c_soil, which sometimes contradict the trends in the reference data shown in the panels in Fig. 1, can be explained by the weaker effect of this parameter compared to the other two. Consequently, the optimal parameters are primarily influenced by entrorg and zvz0i, with c_soil adjusting accordingly.
3.4 Optimization based on output fields
In contrast to the previous section, here we base the optimization on the full 2D output fields of ICON. Figure 7 shows the histograms of the optimized model parameters using the weight uncertainty method from Sect. 2.4, in direct analogy to the QoI optimization (Fig. 4). The optimized parameters generally scatter close to their default values, with slightly lower values for entrorg, slightly larger values for zvz0i, and lower values for c_soil. Thus, the default parameters already appear to provide a reasonable balance across all output variables for the specified time and region, given the weight ranges from Table 1. The parameter values for entrorg and zvz0i are more concentrated compared to c_soil, again highlighting their greater impact on the variables, which is supported by the stronger magnitudes in the spatial variability fields (Fischer et al., 2024, compare their Fig. 7 to their Figs. 8 and 9). These variability fields in comparison to the target difference fields in Fig. 2(c) offer insight into whether the desired target change in a specific variable could be achieved by changing individual model parameters. However, the spatial patterns in this comparison differ strongly for several variables such as precipitation; column-integrated water vapor; 2 m temperature; 2 m dew point temperature; MSLP; and, to a lesser extent, wind speeds. This suggests that modifying individual model parameters would not lead to an overall improvement over the whole domain. For precipitation, changes in parameters primarily induce zonally oriented alterations (Figs. 7(a4) and (b4) and 9(f4) in Fischer et al., 2024), which do not correspond with the target differences, particularly over mountainous regions such as the Guinea Highlands and the Cameroon line. This discrepancy may be attributed to the representation of convection, which is parameterized in our ICON configuration. Although parameterized convection can produce realistic rainfall amounts over Africa (e.g., Kniffka et al., 2019), spatial discrepancies remain pronounced (Fig. 2(c1)). It likely also relates to the spatial resolution, which struggles with complex topography and coastal dynamics. These discrepancies therefore necessitate alternative approaches, such as increasing the resolution in simulations and improving the physical representations within the model.
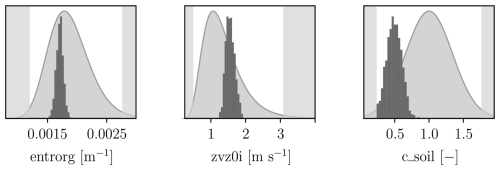
Figure 7Histograms of optimal model parameters as a result of Monte Carlo simulations with weights from Table 1 for optimizing output fields.
For other variables, although the patterns of spatial variability fields for certain parameters exhibit some correlation with the target difference field, the prospects of attaining a combined optimal state for all variables remain limited. This limitation arises when the desired directions of change across variables do not align with the directions caused by a parameter change. An illustrative example of this effect is 2 m temperature and 2 m dew point temperature. Enhancing c_soil leads to more evaporation and thus lower low-level temperatures and higher dew point temperatures (see Fig. 1, opposite sign). However, as the differences between ICON and ERA5 are largely of the same sign (Fig. 2(2c) and (3c)), this disagreement cannot be reconciled by changing c_soil. Therefore, adjusting the three parameters remains insufficient for reducing the regional discrepancies between the ICON model outputs and the reference data.
Finally, Fig. 8 depicts the optimized parameters when varying the weights assigned to the output variables in analogy to Fig. 6 for the QoI optimization. Notable differences from the QoI optimization include the increase in the optimal entrainment rate for high weights on precipitation and high-level clouds, suggesting that a higher entrainment rate can better address regional changes in these variables but not the domain average. Particularly for precipitation, the increase over the Guinea Highlands and the decrease over the eastern Gulf of Guinea for enhanced entrainment rates are dominant (Fig. 7(a4) in Fischer et al., 2024), which controls the optimization towards the reference data (Fig. 2(1c)). Other dependencies of optimal model parameters on assigned weights and discrepancies between the two optimization strategies provide insight for developers to improve parameter definitions or understand their effects. However, these findings should not be overinterpreted, given the limited domain and parameter set of this study.
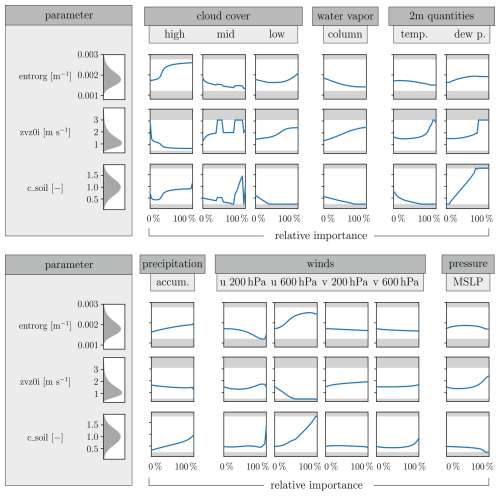
Figure 8Optimal model parameters resulting from MOO. Weights (relative importance) for individual output fields are successively increased, while weights for all other output fields are specified based on their mean values in Table 1, summing to 100 %. A separate optimization problem is solved for each weight combination.
Simulating the West African monsoon with numerical weather and climate models remains a significant challenge. This study aimed to reduce errors in ICON model simulations over the WAM region during the boreal summer by adjusting three uncertain model parameters that have been found to have a strong effect on WAM characteristics: the entrainment rate, the terminal fall speed of ice crystals, and the soil moisture evaporation fraction. The optimization goal was to better align the ICON model output with reference data from ERA5 reanalysis and GPM IMERG for precipitation.
We employed surrogate models using PCA and Gaussian process regression for full 2D output fields and QoIs. By assigning weights based on expert opinion to reflect their relative importance, we solved the surrogate-based optimization problem in a computationally efficient manner. To account for variations in optima due to changes in the weights, we employed two strategies: inducing spread in the weights and varying the weights individually.
Our findings indicate that the model parameters are generally well-tuned in the default model setup, even if the optimal values strongly depend on the weights of the meteorological variables in the optimization process. However, the optimal state for the entrainment rate is extremely low when considering QoIs. This suggests that lower entrainment rates better capture averaged WAM dynamics, including increased rainfall, higher 2 m dew points, and a weaker SHL. When optimizing the full 2D output fields, the default parameters already represent a relatively good balance. For most meteorological variables, parameter changes result in pattern changes that do not align with the desired pattern changes to approximate reference data, indicating that these parameters cannot account for the spatial discrepancies. Furthermore, even when there is some correlation in these spatial patterns, improving the accuracy in certain variables invariably leads to a deterioration in others.
Despite these limitations, this study has developed powerful tools for MOO, applicable across various scientific disciplines. These tools aid in understanding the impact of varying objective weights on optimal parameters and corresponding QoIs. In meteorology, this study has highlighted the constraints of parameter tuning, particularly in regions affected by diverse factors such as complex topography or coastal dynamics. To improve model accuracy further, other strategies should be explored, such as increasing spatial resolution, improving the representation of physical processes, or adopting fundamentally different approaches like artificial intelligence for weather and climate prediction.
Within the context of this paper, an interactive tool has been developed that employs the surrogate models for full 2D output fields to visualize the effect of parameter changes on output fields. Additionally, it allows for the visualization of the differences between the model output for these parameters and the reference data. The online tool is accessible at https://mattfis.github.io/wam-simulations/ (last access: 13 January 2025, https://doi.org/10.5281/zenodo.11505849, Fischer, 2024). Note that the surrogate model has been developed for the six original model parameters. However, in the optimization studies presented in this paper, only the three considered parameters with the largest sensitivities are optimized, while the other three parameters are set to their default values. The computational framework used in this study primarily relies on publicly available software packages, along with custom extensions. Optimization analyses were performed using the SciPy package for Python (https://github.com/scipy/scipy, Virtanen et al., 2020). PCA was performed using the “scikit-learn” package for Python (https://github.com/scikit-learn/scikit-learn, Pedregosa et al., 2011).
The reference data used in this study include the ERA5 reanalysis data (https://doi.org/10.24381/cds.bd0915c6 (Hersbach et al., 2023a) and https://doi.org/10.24381/cds.adbb2d47 (Hersbach et al., 2023b) and the GPM IMERG precipitation data (https://doi.org/10.5067/GPM/IMERG/3B-HH/07, Huffman et al., 2019). These datasets are publicly available and have been widely utilized in the meteorological research community.
MF designed the study, including the optimization strategies and surrogate models, with input from all co-authors. PK provided guidance on the meteorological steps required for the analysis and contributed to the meteorological setup and interpretation of results. CP contributed to the methodological aspects of the study, including the development of surrogate models and optimization strategies. MF prepared the paper with input from all co-authors.
At least one of the (co-)authors is a member of the editorial board of Weather and Climate Dynamics. The peer-review process was guided by an independent editor, and the authors also have no other competing interests to declare.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims made in the text, published maps, institutional affiliations, or any other geographical representation in this paper. While Copernicus Publications makes every effort to include appropriate place names, the final responsibility lies with the authors.
Peter Knippertz acknowledges project C2 “Prediction of wet and dry periods of the West African Monsoon’’ of the Transregional Collaborative Research Center SFB/TRR 165 “Waves to Weather’’ funded by the German Science Foundation (DFG).
This research has been supported by the Deutsche Forschungsgemeinschaft (C2; grant no. SFB/TRR 165).
This paper was edited by Tim Woollings and reviewed by two anonymous referees.
Bellprat, O., Kotlarski, S., Lüthi, D., and Schär, C.: Objective calibration of regional climate models, J. Geophys. Res.-Atmos., 117, 23115, https://doi.org/10.1029/2012jd018262, 2012. a
Chang, W., Applegate, P. J., Haran, M., and Keller, K.: Probabilistic calibration of a Greenland Ice Sheet model using spatially resolved synthetic observations: toward projections of ice mass loss with uncertainties, Geosci. Model Dev., 7, 1933–1943, https://doi.org/10.5194/gmd-7-1933-2014, 2014. a
Cinquegrana, D., Zollo, A. L., Montesarchio, M., and Bucchignani, E.: A Metamodel-Based Optimization of Physical Parameters of High Resolution NWP ICON-LAM over Southern Italy, Atmosphere, 14, 788, https://doi.org/10.3390/atmos14050788, 2023. a
Cook, K. H. and Vizy, E. K.: Coupled Model Simulations of the West African Monsoon System: Twentieth- and Twenty-First-Century Simulations, J. Climate, 19, 3681–3703, https://doi.org/10.1175/jcli3814.1, 2006. a
Couvreux, F., Hourdin, F., Williamson, D., Roehrig, R., Volodina, V., Villefranque, N., Rio, C., Audouin, O., Salter, J., Bazile, E., Brient, F., Favot, F., Honnert, R., Lefebvre, M.-P., Madeleine, J.-B., Rodier, Q., and Xu, W.: Process-Based Climate Model Development Harnessing Machine Learning: I. A Calibration Tool for Parameterization Improvement, J. Adv. Model. Earth Sy., 13, e2020MS002217, https://doi.org/10.1029/2020MS002217, 2021. a, b
Deutscher Wetterdienst (DWD): ICON Namelist Overview, Tech. rep., 2019. a
Fink, A. H., Engel, T., Ermert, V., van der Linden, R., Schneidewind, M., Redl, R., Afiesimama, E., Thiaw, W. M., Yorke, C., Evans, M., and Janicot, S.: Mean Climate and Seasonal Cycle, in: Meteorology of Tropical West Africa, 39 pp., John Wiley & Sons, Ltd, https://doi.org/10.1002/9781118391297.ch1, 2017. a
Fischer, M.: mattfis/wam-simulations: v1.0.2, Zenodo [code], https://doi.org/10.5281/zenodo.11505849, 2024. a
Fischer, M. and Proppe, C.: Enhanced universal kriging for transformed input parameter spaces, Probabilistic Eng. Mech., 74, 103486, https://doi.org/10.1016/j.probengmech.2023.103486, 2023. a, b
Fischer, M., Knippertz, P., van der Linden, R., Lemburg, A., Pante, G., Proppe, C., and Marsham, J. H.: Quantifying uncertainty in simulations of the West African monsoon with the use of surrogate models, Weather Clim. Dynam., 5, 511–536, https://doi.org/10.5194/wcd-5-511-2024, 2024. a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r
Flohn, H.: Investigations on the Tropical Easterly Jet, Bonner meteorologische Abhandlungen, Dümmlers, 1964. a
Gong, W., Duan, Q., Li, J., Wang, C., Di, Z., Ye, A., Miao, C., and Dai, Y.: Multiobjective adaptive surrogate modeling‐based optimization for parameter estimation of large, complex geophysical models, Water Resour. Res., 52, 1984–2008, https://doi.org/10.1002/2015wr018230, 2016. a
Haile, M.: Weather patterns, food security and humanitarian response in sub-Saharan Africa, Philos. T. R. Soc. B, 360, 2169–2182, https://doi.org/10.1098/rstb.2005.1746, 2005. a
Hall, N. M. and Peyrillé, P.: Dynamics of the West African monsoon, J. Phys. IV, 139, 81–99, https://doi.org/10.1051/jp4:2006139007, 2006. a
Hannak, L., Knippertz, P., Fink, A. H., Kniffka, A., and Pante, G.: Why Do Global Climate Models Struggle to Represent Low-Level Clouds in the West African Summer Monsoon?, J. Climate, 30, 1665–1687, https://doi.org/10.1175/jcli-d-16-0451.1, 2017. a
Hastenrath, S.: Climate Dynamics of the Tropics, Springer Netherlands, https://doi.org/10.1007/978-94-011-3156-8, 1991. a
Hersbach, H., Bell, B., Berrisford, P., Hirahara, S., Horányi, A., Muñoz-Sabater, J., Nicolas, J., Peubey, C., Radu, R., Schepers, D., Simmons, A., Soci, C., Abdalla, S., Abellan, X., Balsamo, G., Bechtold, P., Biavati, G., Bidlot, J., Bonavita, M., Chiara, G., Dahlgren, P., Dee, D., Diamantakis, M., Dragani, R., Flemming, J., Forbes, R., Fuentes, M., Geer, A., Haimberger, L., Healy, S., Hogan, R. J., Hólm, E., Janisková, M., Keeley, S., Laloyaux, P., Lopez, P., Lupu, C., Radnoti, G., Rosnay, P., Rozum, I., Vamborg, F., Villaume, S., and Thépaut, J.-N.: The ERA5 global reanalysis, Q. J. Roy. Meteor. Soc., 146, 1999–2049, https://doi.org/10.1002/qj.3803, 2020. a
Hersbach, H., Bell, B., Berrisford, P., Biavati, G., Horányi, A., Muñoz Sabater, J., Nicolas, J., Peubey, C., Radu, R., Rozum, I., Schepers, D., Simmons, A., Soci, C., Dee, D., and Thépaut, J.-N.: ERA5 hourly data on pressure levels from 1940 to present, Climate Data Store [data set], https://doi.org/10.24381/cds.bd0915c6, 2023a.
Hersbach, H., Bell, B., Berrisford, P., Biavati, G., Horányi, A., Muñoz Sabater, J., Nicolas, J., Peubey, C., Radu, R., Rozum, I., Schepers, D., Simmons, A., Soci, C., Dee, D., and Thépaut, J.-N.: ERA5 hourly data on single levels from 1940 to present, Climate Data Store [data set], https://doi.org/10.24381/cds.adbb2d47, 2023b.
Huffman, G., Stocker, E., Bolvin, D., Nelkin, E., and Tan, J.: GPM IMERG final precipitation L3 half hourly 0.1 degree x 0.1 degree V06, Goddard Earth Sciences Data and Information Services Center (GES DISC): Greenbelt, MD, USA [data set], https://doi.org/10.5067/GPM/IMERG/3B-HH/07, 2019. a, b
Jolliffe, I. T.: Principal Component Analysis, Springer New York, ISBN 9781475719048, https://doi.org/10.1007/978-1-4757-1904-8, 1986. a
Kendon, E. J., Stratton, R. A., Tucker, S., Marsham, J. H., Berthou, S., Rowell, D. P., and Senior, C. A.: Enhanced future changes in wet and dry extremes over Africa at convection-permitting scale, Nat. Commun., 10, 1794, https://doi.org/10.1038/s41467-019-09776-9, 2019. a
Kniffka, A., Knippertz, P., and Fink, A. H.: The role of low-level clouds in the West African monsoon system, Atmos. Chem. Phys., 19, 1623–1647, https://doi.org/10.5194/acp-19-1623-2019, 2019. a, b, c
Kniffka, A., Knippertz, P., Fink, A. H., Benedetti, A., Brooks, M. E., Hill, P. G., Maranan, M., Pante, G., and Vogel, B.: An evaluation of operational and research weather forecasts for southern West Africa using observations from the DACCIWA field campaign in June–July 2016, Q. J. Roy. Meteor. Soc., 146, 1121–1148, https://doi.org/10.1002/qj.3729, 2020. a, b, c
Lavaysse, C., Flamant, C., Janicot, S., Parker, D. J., Lafore, J.-P., Sultan, B., and Pelon, J.: Seasonal evolution of the West African heat low: a climatological perspective, Clim. Dynam., 33, 313–330, https://doi.org/10.1007/s00382-009-0553-4, 2009. a
Lebel, T. and Ali, A.: Recent trends in the Central and Western Sahel rainfall regime (1990–2007), J. Hydrol., 375, 52–64, https://doi.org/10.1016/j.jhydrol.2008.11.030, 2009. a
Lebel, T., Diedhiou, A., and Laurent, H.: Seasonal cycle and interannual variability of the Sahelian rainfall at hydrological scales, J. Geophys. Res., 108, 8389, https://doi.org/10.1029/2001jd001580, 2003. a
Lee, L. A., Reddington, C. L., and Carslaw, K. S.: On the relationship between aerosol model uncertainty and radiative forcing uncertainty, P. Natl. Acad. Sci. USA, 113, 5820–5827, https://doi.org/10.1073/pnas.1507050113, 2016. a
Lu, D., Ricciuto, D., Stoyanov, M., and Gu, L.: Calibration of the E3SM Land Model Using Surrogate-Based Global Optimization, J. Adv. Model. Earth Sy., 10, 1337–1356, https://doi.org/10.1002/2017MS001134, 2018. a
Marsham, J. H., Dixon, N. S., Garcia-Carreras, L., Lister, G. M. S., Parker, D. J., Knippertz, P., and Birch, C. E.: The role of moist convection in the West African monsoon system: Insights from continental-scale convection-permitting simulations, Geophys. Res. Lett., 40, 1843–1849, https://doi.org/10.1002/grl.50347, 2013. a
Martin, G. M., Peyrillé, P., Roehrig, R., Rio, C., Caian, M., Bellon, G., Codron, F., Lafore, J.-P., Poan, D. E., and Idelkadi, A.: Understanding the West African Monsoon from the analysis of diabatic heating distributions as simulated by climate models, J. Adv. Model. Earth Sy., 9, 239–270, https://doi.org/10.1002/2016ms000697, 2017. a
Mathon, V., Laurent, H., and Lebel, T.: Mesoscale Convective System Rainfall in the Sahel, J. Appl. Meteorol., 41, 1081–1092, https://doi.org/10.1175/1520-0450(2002)041<1081:mcsrit>2.0.co;2, 2002. a
Messager, C., Gallée, H., and Brasseur, O.: Precipitation sensitivity to regional SST in a regional climate simulation during the West African monsoon for two dry years, Clim. Dynam., 22, 249–266, https://doi.org/10.1007/s00382-003-0381-x, 2004. a
Neelin, J. D., Bracco, A., Luo, H., McWilliams, J. C., and Meyerson, J. E.: Considerations for parameter optimization and sensitivity in climate models, P. Natl. Acad. Sci. USA, 107, 21349–21354, https://doi.org/10.1073/pnas.1015473107, 2010. a
Nicholson, S. E.: A revised picture of the structure of the “monsoon” and land ITCZ over West Africa, Clim. Dynam., 32, 1155–1171, https://doi.org/10.1007/s00382-008-0514-3, 2009. a
Ollinaho, P., Järvinen, H., Bauer, P., Laine, M., Bechtold, P., Susiluoto, J., and Haario, H.: Optimization of NWP model closure parameters using total energy norm of forecast error as a target, Geosci. Model Dev., 7, 1889–1900, https://doi.org/10.5194/gmd-7-1889-2014, 2014. a
Pante, G. and Knippertz, P.: Resolving Sahelian thunderstorms improves mid-latitude weather forecasts, Nat. Commun., 10, 3487, https://doi.org/10.1038/s41467-019-11081-4, 2019. a
Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V., Thirion, B., Grisel, O., Blondel, M., Prettenhofer, P., Weiss, R., Dubourg, V., Vanderplas, J., Passos, A., Cournapeau, D., Brucher, M., Perrot, M., and Duchesnay, E.: Scikit-learn: Machine Learning in Python, J. Mach. Learn. Res., 12, 2825–2830, https://jmlr.org/beta/papers/v12/pedregosa11a.html (last access: 20 January 2025), 2011 (code available at: https://github.com/scikit-learn/scikit-learn, last access: 20 January 2025). a
Rasmussen, C. E. and Williams, C. K. I.: Gaussian Processes for Machine Learning, The MIT Press, https://doi.org/10.7551/mitpress/3206.001.0001, 2005. a
Ray, J., Hou, Z., Huang, M., Sargsyan, K., and Swiler, L.: Bayesian Calibration of the Community Land Model Using Surrogates, SIAM/ASA Journal on Uncertainty Quantification, 3, 199–233, https://doi.org/10.1137/140957998, 2015. a
Ruiz, J. J., Pulido, M., and Miyoshi, T.: Estimating Model Parameters with Ensemble-Based Data Assimilation: A Review, J. Meteorol. Soc. Jpn., 91, 79–99, https://doi.org/10.2151/jmsj.2013-201, 2013. a, b
Sanderson, B. M., Piani, C., and Ingram, W. J.: Towards constraining climate sensitivity by linear analysis of feedback patterns in thousands of perturbed-physics GCM simulations, Clim. Dynam., 30, 175–190, https://doi.org/10.1007/s00382-007-0280-7, 2008. a
Sexton, D., Murphy, J., Collins, M., and Webb, M.: Multivariate Probabilistic Projections Using Imperfect Climate Models. Part I: Outline of Methodology, Clim. Dynam., 38, 1–30, https://doi.org/10.1007/s00382-011-1208-9, 2011. a
Shafii, M. and De Smedt, F.: Multi-objective calibration of a distributed hydrological model (WetSpa) using a genetic algorithm, Hydrol. Earth Syst. Sci., 13, 2137–2149, https://doi.org/10.5194/hess-13-2137-2009, 2009. a
Stainforth, D., Aina, T., Christensen, C., Collins, M., Faull, N., Frame, D., Kettleborough, J., Knight, S., Martin, A., Murphy, J., Piani, C., Sexton, D., Smith, L., Spicer, R., Thorpe, A., and Allen, M.: Uncertainty in predictions of the climate response to rising levels of greenhouse gases, Nature, 433, 403–406, https://doi.org/10.1038/nature03301, 2005. a
Tchotchou, L. A. D. and Kamga, F. M.: Sensitivity of the simulated African monsoon of summers 1993 and 1999 to convective parameterization schemes in RegCM3, Theor. Appl. Climatol., 100, 207–220, https://doi.org/10.1007/s00704-009-0181-2, 2009. a
Thorncroft, C. D., Nguyen, H., Zhang, C., and Peyrillé, P.: Annual cycle of the West African monsoon: regional circulations and associated water vapour transport, Q. J. Roy. Meteor. Soc., 137, 129–147, https://doi.org/10.1002/qj.728, 2011. a
Vellinga, M., Arribas, A., and Graham, R.: Seasonal forecasts for regional onset of the West African monsoon, Clim. Dynam., 40, 3047–3070, https://doi.org/10.1007/s00382-012-1520-z, 2013. a
Virtanen, P., Gommers, R., Oliphant, T. E., Haberland, M., Reddy, T., Cournapeau, D., Burovski, E., Peterson, P., Weckesser, W., Bright, J., van der Walt, S. J., Brett, M., Wilson, J., Millman, K. J., Mayorov, N., Nelson, A. R. J., Jones, E., Kern, R., Larson, E., Carey, C. J., Polat, İ., Feng, Y., Moore, E. W., VanderPlas, J., Laxalde, D., Perktold, J., Cimrman, R., Henriksen, I., Quintero, E. A., Harris, C. R., Archibald, A. M., Ribeiro, A. H., Pedregosa, F., van Mulbregt, P., and SciPy 1.0 Contributors: SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python, Nat. Methods, 17, 261–272, https://doi.org/10.1038/s41592-019-0686-2, 2020 (code available at: https://github.com/scipy/scipy, last access: 20 January 2025). a, b
Watson-Parris, D., Williams, A., Deaconu, L., and Stier, P.: Model calibration using ESEm v1.1.0 – an open, scalable Earth system emulator, Geosci. Model Dev., 14, 7659–7672, https://doi.org/10.5194/gmd-14-7659-2021, 2021. a, b
Williamson, D., Goldstein, M., Allison, L., Blaker, A., Challenor, P., Jackson, L., and Yamazaki, K.: History matching for exploring and reducing climate model parameter space using observations and a large perturbed physics ensemble, Clim. Dynam., 41, 1703–1729, https://doi.org/10.1007/s00382-013-1896-4, 2013. a
Xue, Y., Sales, F. D., Lau, W. K.-M., Boone, A., Feng, J., Dirmeyer, P., Guo, Z., Kim, K.-M., Kitoh, A., Kumar, V., Poccard-Leclercq, I., Mahowald, N., Moufouma-Okia, W., Pegion, P., Rowell, D. P., Schemm, J., Schubert, S. D., Sealy, A., Thiaw, W. M., Vintzileos, A., Williams, S. F., and Wu, M.-L. C.: Intercomparison and analyses of the climatology of the West African Monsoon in the West African Monsoon Modeling and Evaluation project (WAMME) first model intercomparison experiment, Clim. Dynam., 35, 3–27, https://doi.org/10.1007/s00382-010-0778-2, 2010. a
Zängl, G.: Adaptive tuning of uncertain parameters in a numerical weather prediction model based upon data assimilation, Q. J. Roy. Meteor. Soc., 149, 2861–2880, https://doi.org/10.1002/qj.4535, 2023. a, b, c
Zängl, G., Reinert, D., Rípodas, P., and Baldauf, M.: The ICON (ICOsahedral Non-hydrostatic) modelling framework of DWD and MPI-M: Description of the non-hydrostatic dynamical core, Q. J. Roy. Meteor. Soc., 141, 563–579, https://doi.org/10.1002/qj.2378, 2015. a, b
Zheng, X. and Eltahir, E. A. B.: The Role of Vegetation in the Dynamics of West African Monsoons, J. Climate, 11, 2078–2096, 1998. a
Zhu, H. and Hendon, H. H.: Role of large-scale moisture advection for simulation of the MJO with increased entrainment, Q. J. Roy. Meteor. Soc., 141, 2127–2136, https://doi.org/10.1002/qj.2510, 2015. a