the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
African easterly waves in an idealized general circulation model: instability and wave packet diagnostics
Joshua White
We examine the group dynamic of African easterly waves (AEWs) generated in a realistic, spatially non-homogeneous African easterly jet (AEJ) using an idealized general circulation model. Our objective is to investigate whether the limited zonal extent of the AEJ is an impediment to AEW development. We construct a series of basic states using global reanalysis fields and initialize waves via transient heating over West Africa. The dominant response is a localized, near-stationary wave packet that disperses upstream and downstream. The inclusion of a crude representation of boundary layer damping stabilizes the waves in most cases, consistent with other studies in the past. In some basic states, however, exponential growth occurs even in the presence of damping. This shows that AEWs can occasionally emerge spontaneously. The key result is that, whether triggered by an external forcing or generated internally, the wave packet can remain within the AEJ for multiple wave periods instead of being swept away. Drawing from other studies, this also suggests that even the damped waves can grow if coupled with additional sources of energy such as moist convection and dust radiative feedback. The wave packet in the localized AEJ appears to satisfy a condition for absolute instability, a form of spatial hydrodynamic instability. However, this needs to be verified more rigorously. We conclude that the limited zonal extent of the AEJ is not an impediment. Our results also suggest that the intermittent nature of AEWs is mediated, not by transitions between convective and absolute instability, but likely by external sources such as propagating equatorial wave modes.
- Article
(8362 KB) - Full-text XML
- BibTeX
- EndNote
African easterly waves (AEWs) are the dominant synoptic-scale feature of the summertime West African monsoon (WAM). The AEW storm track extends across the southern and northern sides of the mid-tropospheric African easterly jet (AEJ). Burpee (1972) showed that the climatological basic state over North Africa is associated with a reversal in the meridional gradient of potential vorticity (PV), satisfying the necessary condition for mixed baroclinic–barotropic instability (Charney and Stern, 1962). He proposed that AEWs are the result of small amplitude disturbances growing on the unstable basic state. In this viewpoint, AEWs amplify at the expense of the background reservoir of zonal kinetic energy and zonal available potential energy (e.g., Hsieh and Cook, 2005). Calculations made using field campaign data have generally supported this notion (e.g., Norquist et al., 1977; Reed et al., 1977). Furthermore, the fastest-growing (or slowest-decaying) normal modes of the AEJ in idealized numerical models appear to have wave number and frequency that are close to observed AEWs (e.g., Rennick, 1976; Simmons, 1977; Thorncroft and Hoskins, 1994; Leroux and Hall, 2009). In this regard, hydrodynamic instability has been a useful model to account for the existence of AEWs.
1.1 Criticisms of linear normal mode instability
In the recent past, the applicability of linear normal mode instability to AEWs has been questioned. Two main criticisms have been put forth. The first one concerns the impact of viscous damping. Hall et al. (2006) showed that AEW growth rates were reduced, or even reversed, by what they take to be realistic levels of damping in an idealized general circulation model. They contended that an AEJ, which is otherwise super-critical to inviscid normal modes, may be stabilized by boundary layer damping. The second criticism concerns the localized nature of the AEJ. As shown by Dickinson and Molinari (2000), the climatological meridional gradient reversal of PV associated with the AEJ during July–October spans around 60–70∘ of longitudes. Some studies have claimed that the zonal extent of the AEJ, and the implied region of instability, is too short to sustain wave growth. Thorncroft et al. (2008) estimated that the AEJ length is no more than twice the wavelength of an AEW. They argued that the limited extent of the AEJ and the stabilizing effect of damping would preclude unstable modes from emerging spontaneously out of background noise. These two lines of argument led Thorncroft et al. (2008) to suggest that large amplitude triggers are necessary for the generation of AEWs.
Whereas Hall et al. (2006) and Thorncroft et al. (2008) used a climatological basic state, Leroux and Hall (2009) used the same model but with 336 different states derived from global reanalysis data. While many of their basic states showed no development, some showed growing waves. They reiterated the conclusion of Thorncroft et al. (2008) regarding the importance of external triggers for AEWs. They also concluded the growth rate of waves was most consistently related not necessarily to the strength of the AEJ but to the vertical wind shear associated with it. In a related study, Leroux et al. (2010) showed that external triggers from extratropics can also account for AEW activity. The triggering hypothesis for AEWs is now a widely accepted view of AEW formation. Yet, it should be noted that there is little doubt that observed and modeled waves appear to be sustained by baroclinic and barotropic energy conversions from the background state of the atmosphere over North Africa (e.g., Norquist et al., 1977; Thorncroft and Hoskins, 1994; Hsieh and Cook, 2007). How does that occur within a zonally limited AEJ? We attempt to address this question.
1.2 Destabilization by moist convection and dust aerosol forcing
While the results of Hall et al. (2006) and Leroux and Hall (2009) have spurred the adoption of the viewpoint that AEWs need an external trigger, at least two critical aspects of the dynamics are missing in their simulations. First, their model had no interactive moist convection. The AEW storm track region of North Africa is home to frequent and intense mesoscale convective systems (e.g., Laing et al., 1999; Fink and Reiner, 2003; Laing et al., 2011). It has been shown that moist convection is essential to account for observed AEW structure and strength (e.g., Mass, 1979; Schwendike and Jones, 2010; Hsieh and Cook, 2008; Mekonnen and Rossow, 2011; Berry and Thorncroft, 2012b; Janiga and Thorncroft, 2014; Tomassini et al., 2017; Russell et al., 2020). Both time-mean and transient moist convection act to destabilize AEWs (Russell and Aiyyer, 2020). Although it can be argued that the basic states used by Hall et al. (2006) and Leroux and Hall (2009) have some imprint of time-mean convection, the lack of wave-coupled moist convection severely underestimates their potential growth rate.
Second, AEWs are also subject to strong aerosol radiative forcing associated with the Saharan mineral dust (SMD) (e.g., Karyampudi and Carlson, 1988). There is increasing evidence that SMD can lead to AEW amplification (Jones et al., 2004; Ma et al., 2012). Grogan et al. (2016) showed that the radiative forcing associated with SMD can enhance the eddy available potential energy (EAPE) such that AEW growth rates can be significantly amplified relative to dust-free conditions. Using analytical solutions and model simulations, Nathan et al. (2017) showed that even a sub-critical AEJ, wherein the background PV gradient is single-signed, can yield AEWs that are destabilized by the SMD. They showed that the radiative–dynamical feedback due to SMD can offset the low-level damping.
Taken together, it can be argued that the destabilizing behavior of moist convection and dust radiative forcing should be an important consideration while addressing the first of the two criticism of linear normal mode instability. This does not imply that finite amplitude triggers have no role to play. Instead, it simply means that they are not necessary as claimed by Hall et al. (2006). It is certainly plausible that disturbances induced by large convective outbreaks and extratropical intrusions can project on the normal modes, yielding weak but finite amplitude waves that can then exponentially grow via dust radiative instability and moist convection. This will crucially depend on how much the external forcing projects on the scale of AEWs. Indeed, Thorncroft et al. (2008) found that the waves in their model were much weaker than observations even though the amplitude of the forcing was of a reasonable scale, representing the action of multiple mesoscale convective systems. They also recognized that coupling with moist convection was needed to account for observed wave amplitudes.
As noted earlier, in the recent past, two arguments against linear normal mode instability have been put forth. The first one regarding the stabilizing effect of frictional damping has been addressed in several studies, as discussed above, by including the effects of moist convection and dust radiative forcing. The second criticism regarding the limited zonal extent of the instability is yet to be convincingly examined. Our objective is to address it by elucidating a key property of the wave packets generated in the localized AEJ.
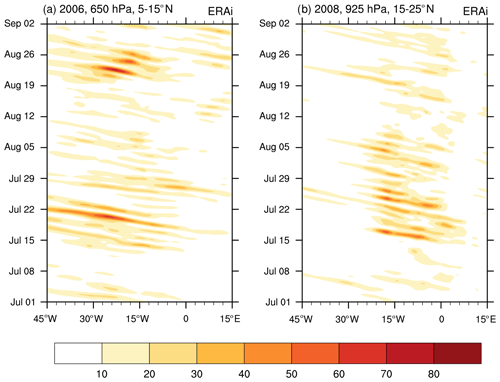
Figure 1Hovmöller diagram of eddy kinetic energy (J kg−1) from ERAI for July–August for the year (a) 2006 at 650 hPa, averaged over 5–15∘ N, and (b) 2008 at 925 hPa, averaged over 15–25∘ N.
2.1 AEW packets
Past studies have established that AEW wavelength (λ), and westward phase speed (cp) are about 3000 km and 10 m s−1 respectively. Estimating the zonal extent (L) of the AEJ to be around 2λ, an approximate residence time is
The argument that the AEJ is too localized (e.g., Thorncroft et al., 2008; Leroux and Hall, 2009) essentially is the statement that a week's time is not sufficient for normal modes to emerge out of background noise. However, an important consideration that is missing from this viewpoint is that the reference speed here should reflect the group propagation instead of the phase. This notion is not new. It has been demonstrated convincingly that extratropical baroclinic eddies are best modeled as modulated wave packets, and their dynamics are intimately tied to their group propagation (e.g., Pierrehumbert, 1984; Mak and Cai, 1989; Orlanski and Katzfey, 1991; Chang et al., 2002; Swanson, 2007). Following this lead, Diaz and Aiyyer (2013a, b) showed that composite AEWs in global reanalysis fields appeared as dispersive wave packets.
Figure 1 shows Hovmöller slices of eddy kinetic energy (EKE) at two different levels. The left panel shows 650 hPa EKE averaged over 5–15∘ N for 2006. The right panel shows 925 hPa EKE averaged over 15–25∘ N for 2008. EKE is calculated using 2–10 d band-pass-filtered winds from the European Centre for Medium-Range Weather Forecasts (ECMWF) interim reanalysis (ERAI). These two levels highlight the northern and southern AEW storm tracks. Both panels of Fig. 1 show distinct wave packets that appear to disperse upstream and downstream. The key observations are that (i) the wave packets are co-located with the AEJ, which extends from about 3∘ W–30∘ E (see Fig. 3), and (ii) the group speed is much smaller than the phase speed. With the group speed as the reference propagation metric, we can estimate the residence time as
and with cg≪cp we have
This relation states that the residence time is mediated by the group propagation dynamic. For a slowly propagating wave packet, it indicates that even a localized AEJ can support growth by the combined effects of the jet instability, moist convection, and SMD radiative forcing. In subsequent sections, we explore the structure of the AEW packet's group speed and the implication for its instability.
An important caveat should be recognized in relation to Fig. 1. We have interpreted it as a pure AEW packet. In nature, however, a variety of tropical and extratropical systems ranging from synoptic (e.g., equatorial waves, breaking extratropical waves) to intraseasonal (the Madden–Julian Oscillation) can modulate the amplitude of AEWs (e.g., Matthews, 2004; Leroux and Hall, 2009; Ventrice et al., 2011; Alaka and Maloney, 2012, 2014). This modulation could, in principle, present itself like the dispersion of a linear wave packet if it leads to preferential amplification on one side of the packet. In a related issue, Aiyyer et al. (2012) showed that cloud signatures associated with tropical cyclones can artificially project onto a wide range of eastward- and westward-propagating equatorial modes as a result of the filtering in the wave-number–frequency domain. The use of an idealized numerical model, wherein the main response is the AEW storm track, mitigates some of this concern and provides an independent assessment of the relevance of group dynamics for observed AEW packets.
2.2 Spatial instability
Using a local kinetic energy budget, Diaz and Aiyyer (2013a) showed that upstream energy dispersion allowed new development within the lagging edge of a slowly propagating AEW packet. Their results also suggested the intriguing potential for the AEJ to support absolute instability, a form of spatial hydrodynamic instability (e.g., Pierrehumbert, 1984; Huerre and Monkewitz, 1990). Herein, both temporal and spatial growth play a role in the development of disturbances. The instability can be classified as either absolute or convective, with the delineation arising due to two possibilities when a disturbance is introduced within an unstable plane-parallel jet (Briggs, 1964; Pierrehumbert, 1984; Dunkerton, 1993).
-
A developing wave packet grows and disperses upstream and downstream of its excitation point. Any fixed point in the domain eventually experiences exponential growth. This situation represents absolute instability and a conceptual illustration for easterly flow in shown in Fig. 2a.
-
A developing wave packet continues to grow but is unable to spread sufficiently upstream and is swept away by the flow such that a fixed point sees growth followed by decay in wave amplitude. This situation represents convective instability and a conceptual illustration for easterly flow in shown in Fig. 2b.
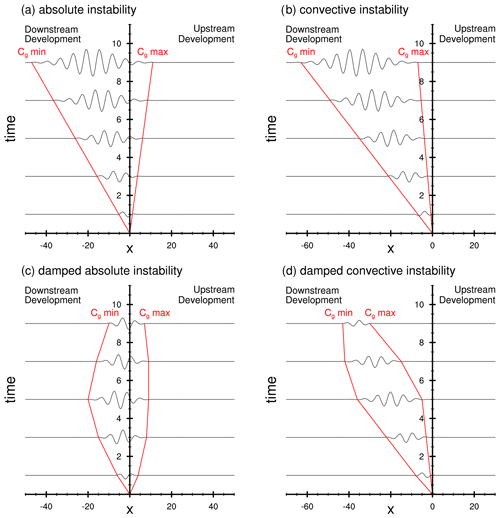
Figure 2Absolute (a, c) and convective (b, d) instability conceptually represented in the x–t plane for an unstable easterly flow. If Cg=0 within the cone, then there is both upstream and downstream development, and the flow is absolutely unstable (a). Otherwise, the flow is convectively unstable (b). If the growth of the wave packet is sufficiently damped as in panels (c) and (d), the amplitude of the wave packet will eventually decay to zero, resulting in weaker waves and a shorter-lived wave packet. Adapted from Diaz and Aiyyer (2015).
When the region of instability is zonally confined, a wave packet that is unable to disperse upstream will cease to grow after it exits this region. On the other hand, with both upstream and downstream dispersion, an absolutely unstable wave packet can continue to grow at all subsequent times. If the basic state cannot support any development, it is deemed stable. It is also possible that a basic state that is unstable under inviscid conditions can be stabilized by damping (e.g., Hall and Sardeshmukh, 1998). In the atmosphere, sources of damping include boundary layer friction, radiative, and convective damping. Thus, in the presence of damping, the growth rate from either of the two spatial instabilities can be reduced or reversed. This is shown in the conceptual diagrams in Fig. 2c and d. We will refer to these situations as damped absolute and convective instabilities respectively.
Diaz and Aiyyer (2015) examined the stability of the zonally uniform version of the climatological AEJ using direct numerical simulations. In their model, a stationary spreading and growing wave packet persisted for several days, even with moderate parameterized damping. They estimated the total group velocity (Cg) following the method described in Orlanski and Chang (1993). In the lieu of a rigorous analytical determination of spatial instability, the heuristic approach (e.g., Orlanski and Chang, 1993) as adapted for easterly waves by Diaz and Aiyyer (2015) is useful:
Based on the analysis of their simulations, Diaz and Aiyyer (2015) claimed that a zonally uniform representation of the AEJ was absolutely unstable. Given that moist convection and dust radiative effects can be additional sources of destabilization, it suggests that absolute instability may be a viable mechanism for the existence of AEWs.
2.3 Hypotheses
Several aspects of the results of Diaz and Aiyyer (2015) ought to be explored further. First, their AEJ did not capture the streamwise inhomogeneity of the observed jet. Second, they only considered a single climatological basic state. They also speculated that the basic states used in Thorncroft et al. (2008), Hall et al. (2006), and Leroux and Hall (2009) were convectively unstable. This is yet to be confirmed. Additionally, Fig. 1 highlights the intermittent AEW activity. Since AEWs tend to propagate in groups, this results in alternate periods of enhanced and reduced synoptic activity. For example during 2006, two distinct wave packets can be seen starting around 14 July and 19 August, with maximum activity just west of −15∘ E. Although Fig. 1 shows only two selected examples, such interspersed episodes of enhanced AEW activity are commonly observed each year. It is of interest to identify factors that mediate this episodic nature of AEW packets. Based on the preceding discussions, we identify two questions and attendant hypotheses to address our objective.
-
How do persistent AEW packets develop in the zonally localized AEJ?
Hypothesis. AEW persistence is related to the generation of a nearly stationary wave packet within a realistic, localized AEJ. This specifically addresses the concern raised in previous studies (e.g., Thorncroft et al., 2008; Leroux and Hall, 2009).
We note that one of the hallmarks of absolute instability is a wave packet that disperses upstream and downstream, with a zero group speed somewhere in the packet. However, a formal determination of absolute instability requires the investigation of the dispersion relationship in the complex plane (e.g., Pierrehumbert, 1984; Dunkerton, 1993). Since that is beyond the scope of this effort, we do not make a formal claim of absolute instability. As in Diaz and Aiyyer (2015), but with a fully varying background flow, we only present a heuristic analysis based on direct numerical simulations.
-
What mediates the vacillation of AEW activity?
Hypothesis. A slowly varying background flow alternates aperiodically in time between supporting stationary and traveling wave packets, leading to the AEW episodes.
In the context of spatial instability, it posits that AEW episodes are mediated by transition between the nature of the instability of the background state (i.e., absolute → convective, and convective → absolute). This also suggests the possibility that intermittent AEW activity may be related to an internal mechanism involving the instability of the AEJ in addition to previously suggested external sources of forcing.
It should be noted that issue of variability of AEW activity mediated by external mechanisms has been examined in several past studies. Leroux et al. (2011) determined that extratropical disturbances from the North Atlantic storm track can influence AEW activity. Others have documented the impact of equatorial Kelvin waves and the Madden–Julian Oscillation on the intraseasonal modulation of AEWs (e.g., Matthews, 2004; Leroux and Hall, 2009; Ventrice et al., 2011; Alaka and Maloney, 2012, 2014). While moist convection has been shown to be important to the evolution of AEWs, in the spirit of retaining only the essence of the dynamics, we do not explicitly account for its feedback in our approach. We test these hypotheses by employing an idealized general circulation model.
We use the University of Reading multilevel primitive equation model configured as described in Hall et al. (2006). We choose this model for several reasons. It is the same model that was used in related studies discussed earlier (Thorncroft et al., 2008; Leroux and Hall, 2009; Leroux et al., 2011). By using a consistent model and experimental approach, we can not only build upon their work but also provide clarification and a novel interpretation of their results. We provide below some information on the model configuration for completeness.
The model has a horizontal spectral resolution of T31 for 10 equally spaced sigma levels. The full nonlinear equations for tendencies of temperature, vorticity, divergence and log (surface pressure) are integrated using a semi-implicit time step of 22.5 min. A ∇6 diffusion is implemented for the momentum and temperature fields. As in Hall et al. (2006), low-level damping is also applied to the momentum and temperature fields, intended as a modest representation of near-surface turbulent heat and momentum transfer. The damping rates in the lower levels linearly decrease from the surface over with an average e-folding timescale of 2 d for momentum and 4 d for temperature. In the free atmosphere (σ<0.8), damping timescales are 10 d for momentum and 30 d for temperature. In addition, we also damp the areas of the globe poleward of 30∘ in both hemispheres to preclude development in the extratropical storm tracks.
Since the model equations are not linearized about a fixed state, a standard approach to maintaining a time-invariant basic state was implemented by Hall et al. (2006). Herein, a forcing term is added to the equations that collectively represent the effects of diabatic heating and transient effects needed to maintain the basic state. The data for the basic state are taken from the National Centers for Environmental Prediction–Department of Energy (NCEP/DOE AMIP II) Reanalysis (Kanamitsu et al., 2002).
3.1 Wave forcing
To excite waves in the AEJ, we force the model with a pulse of localized heating following the method of Thorncroft et al. (2008). The heat source (H) is placed at 15∘ N, 20∘ E and is switched off after 24 h into the simulation. This heating is meant to represent the latent heat release associated with several mesoscale convective systems (MCSs) and is defined as
where r is the horizontal radius and r0 is the horizontal bounding radius of the heating with a distance of 5∘ longitude and latitude. H0 is the deep convective profile from Thorncroft et al. (2008) defined as
The vertically integrated heating rate for this heating is 5 K d−1, corresponding to a peak rain rate of 20 mm d−1. The initial heating is scaled by a factor of 10−4 to ensure consistency with linearization about a fixed basic state. The resulting perturbations are later scaled up by the same factor for display.
To reiterate, we use the same method of initiating waves in a fixed basic state as was done by Thorncroft et al. (2008) and Leroux and Hall (2009) to specifically address the concerns raised by them. Our conclusions are not sensitive to the choice of a wave maker in the model. We have forced the model with red noise and other localized perturbations (e.g., finite amplitude Gaussian vortex) and reach the same conclusion as presented in subsequent sections.
3.2 Simulations
All simulations span 100 d. To quantify wave amplitude, we use the standard definition of eddy kinetic energy (EKE):
where v represents the perturbation velocity field. We define a quantity β as the ratio
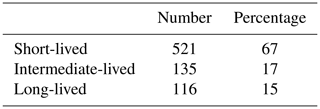
where the square brackets denote averaging over 5–20∘ N and is the maximum EKE within the first 24 h. β is not a growth rate but rather a convenient measure of the strength of the wave packet at any given time relative to the energy input by the initial transient thermal forcing. We use it to classify the longevity of wave packets. If at the lagging edge within the first 20 d, it is classified as short-lived. If for longer than 20 d but less than the full 100 d of the simulation, it is classified as intermediate-lived, and if it for the full simulation, it is classified as long-lived. This method of classification does not require that the fastest-growing or slowest-decaying normal mode be isolated within the simulation period. We examine the evolution of wave packets in the following three basic state configurations.
-
Climatological basic state. This has a June–September mean over 1987–2017.
-
Individual basic states. These were created using 15 d averages, with 5 d overlap, for the same period as above. This yields 775 distinct basic states. Within each year, they represent slow and continuously evolving background flow. This approach of using a sequence of basic states taken from the reanalysis data is similar to Leroux and Hall (2009), who examined a series of basic states taken from global reanalysis. However, their focus was on global temporal growth rates of waves, and they did not perform any spatial diagnostics of the AEW packets.
-
Ensemble-averaged basic states. Out of the 775 individual basic states, subsets based on wave packet longevity are averaged to create three additional basic states. These correspond to the ensemble-averaged short-, intermediate-, and long-lived basic states.
In total, the model is run 779 times with different basic states derived as above.
Each simulation results in one distinct wave packet. Of those, 521 (67 %) are short-lived, 135 (17 %) are intermediate-lived, and 116 (15 %) are long-lived (Table 1). For brevity, we focus on the results from the climatological and ensemble-averaged basic states.
4.1 Climatological basic state
We begin with the response to transient heating imposed on the climatological basic state. Figure 3 shows the basic state zonal winds at σ=0.65 and a latitude–height cross section averaged over 15∘ W–15∘ E. The panels show the zonally localized AEJ peaking around 12–15∘ N and around 600 hPa along the vertical. The monsoon westerlies are located near the surface. The outcome of this simulation is consistent with Thorncroft et al. (2008). During the first 2 d of the simulation, the fixed-heating produces a baroclinic vortex directly where it is applied. Subsequently, a series of perturbations resembling observed AEWs emerges. Figure 4 shows the resulting perturbation streamfunction at hPa) and 0.65(≈650 hPa) on days 5, 11, 17, and 23. The individual phases propagate westward, but the wave packet remains nearly stationary and slowly decays. Figure 5a shows a Hovmöller diagram of the EKE, averaged over 5–20∘ N during the first 40 d of this simulation. The EKE falls below 10 % of its initial value by day 20. Therefore, we classify the resulting wave packet within the climatological basic state as short-lived.
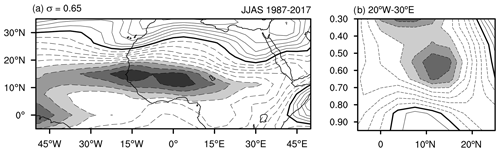
Figure 3JJAS 1987–2017 averaged climatological zonal winds ( m s−1 shaded and negative values dashed) for (a) σ=0.65 level and (b) latitude–height cross section averaged over 15∘ W–15∘ E.
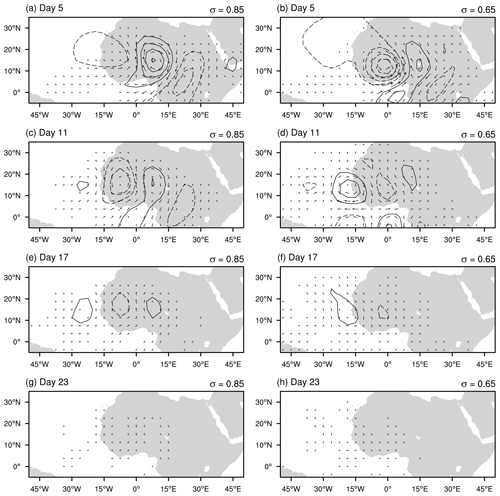
Figure 4Streamfunction (interval 1×105 m2 s−1 with negative values dashed) and horizontal wind vectors at σ=0.85 (a, c, e, g) and 0.65 (b, d, f, h) showing the wave response within the climatological composite basic state for days 5, 11, 17, and 23 from top to bottom.
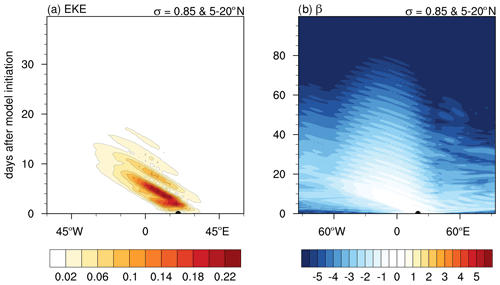
Figure 5Hovmöller diagram of EKE (a, J kg−1) and β (b) at σ=0.65 resulting from fixed heating on the JJAS 1987–2017 composite basic state averaged over 5–20∘ N. Note the difference in times shown between panel (a) and panel (b). The black semicircle at time 0 days represents the location of the initial heating perturbation.
Figure 5b illustrates the parameter β calculated using Eq. (8) for the full duration of the simulation. It shows that even though the wave packet was decaying, it was not swept out of the region, and its structure persisted near 0∘ E. This suggests that the ground-relative group speed was zero within the wave packet, which is one of the conditions associated with absolute instability (Eq. 4). Importantly, as often seen in observations (see Fig. 1 here; and Diaz and Aiyyer, 2013a, 2015), the AEW packet is stationary within the AEJ over West Africa. Calculations of energy budget confirm that barotropic and baroclinic energy conversions from the basic state are both sources of EKE (not shown). However, the presence of damping in the model leads to the eventual decay of the wave packet. This is consistent with the picture of damped absolute instability (Fig. 2c).
4.2 Wave responses for the ensemble-averaged categories
We now consider the ensemble-average basic states for the short-, intermediate-, and long-lived wave packets. The zonal winds at σ=0.65 and a height–latitude cross section for the three basic states are shown in Fig. 6. The basic-state AEJ gets progressively stronger and shifts equatorward, moving from short- to long-lived wave packets. The jet in the former reaches a peak of about 9 m s−1 and in the latter about 10 m s−1. As the AEJ is more directly above the surface westerlies and stronger in the long-lived basic state, both horizontal and vertical wind shear are enhanced as compared to the other two basic states (Fig. 6). Therefore, we anticipate that both barotropic and baroclinic conversion rates will be highest in this basic state. Each of these basic states yields quite similar reversals in the meridional PV gradient (not shown), which are capable of supporting the development of AEWs through mixed barotropic–baroclinic instability. Consistent with it, energy budgets confirm barotropic and baroclinic energy conversions from the basic state (not shown).
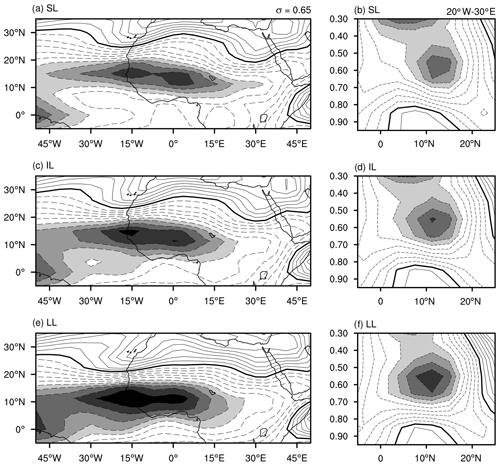
Figure 6Zonal winds ( m s−1 shaded with negative values dashed) at σ=0.65 (a, c, e) and latitude–height cross section averaged over −15 to 15∘ E (b, d, f) for the short-, intermediate-, and long-lived basic states.
As in the climatological case, each ensemble-average basic state generates a series of disturbances that resemble AEW packets. Figure 7 shows short-lived response for days 5–23, separated by roughly one wave period. On day 5, the streamfunction field shows waves with horizontal tilt consistent with barotropic instability. The wave packet has its peak amplitude around 0∘ E. On day 11, the amplitude has dropped substantially, and by day 23, the streamfunction fails to reach the minimum contour used in the figure. Figure 8 shows the evolution of the intermediate-lived wave packet. The streamfunction on day 5 closely resembles the same for the short-lived wave packet but with greater amplitude. This suggests that the basic state for intermediate-lived wave packet permits larger growth rates. By day 11, the wave packet is still present but has undergone some damping, although not nearly to the same extent of the short-lived wave packet. On day 17, the wave packet persists but is weaker. By day 23, the AEW packet has further diminished. Figure 9 shows the evolution of the long-lived wave packet. As opposed to the short- and intermediate-lived wave packets, this one continues to grow at all subsequent times after initiation. The waves are tilted upshear in both the horizontal and vertical planes, indicating barotropic and baroclinic energy conversions.
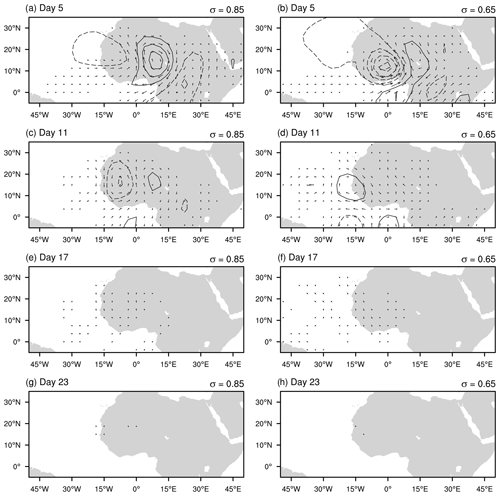
Figure 7Streamfunction (interval 1×105 m2 s−1 with negative values dashed) and horizontal wind vectors at σ=0.85 (a, c, e, g) and 0.65 (b, d, f, h) showing the wave response within the short-lived basic state for days 5, 11, 17, and 23 from top to bottom.
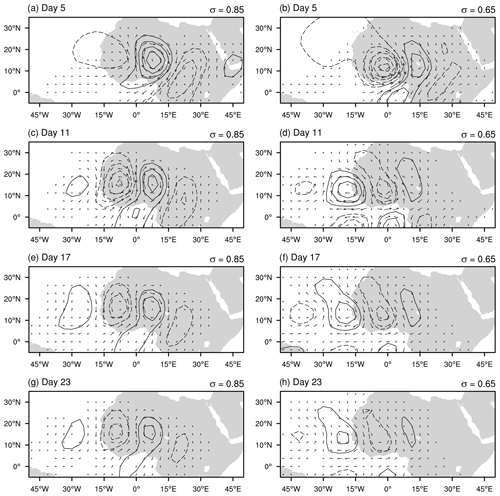
Figure 8Streamfunction (interval 1×105 m2 s−1 with negative values dashed) and horizontal wind vectors at σ=0.85 (a, c, e, g) and 0.65 (b, d, f, h) showing the wave response within the intermediate-lived basic state for days 5, 11, 17, and 23 from top to bottom.
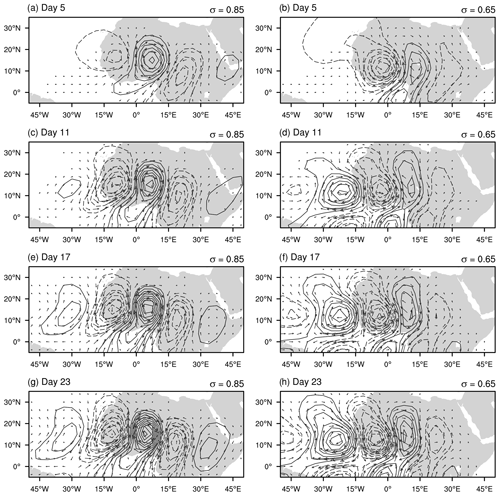
Figure 9Streamfunction (interval 1×105 m2 s−1 with negative values dashed) and horizontal wind vectors at σ=0.85 (a, c, e, g) and 0.65 (b, d, f, h) showing the wave response within the long-lived basic state for days 5, 11, 17, and 23 from top to bottom.
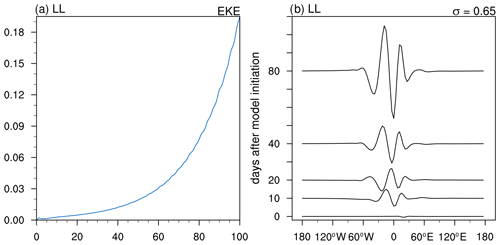
Hovmöller diagrams for EKE and β for these three simulations are shown in Fig. 10. The former is shown for the first 30 d, while the latter is shown for the full 100 d of the simulation. The location of the center of the transient heating is shown using a black dot. The EKE panels for the short- and intermediate-lived cases show damped wave packets, while the long-lived panel shows an amplifying wave packet. Owing to the logarithmic definition of β, we can see the behavior of the wave packets long after the transient heating. Initially, the response is a baroclinic vortex that projects on a wide range of modes. Some of those are advected out of the localized region of instability and damped. In the short-lived case, the wave packet that remains is much weaker and is not sustained by barotropic–baroclinic energy conversions against the imposed frictional damping. This is illustrated by the progressively negative values of β within the vicinity of 0∘ E. After 60 d, the wave packet amplitude is indistinguishable from noise in the model. In the intermediate-lived simulation, the damping does not diminish the wave packet as quickly. As a result, the wave packet is visible throughout its lifetime. However, the EKE drops below 10 % of its original value by day 40. The long-lived case shows a growing, expanding wave packet. By the end of the simulation, its amplitude reaches 2 orders of magnitude higher than its initial value.
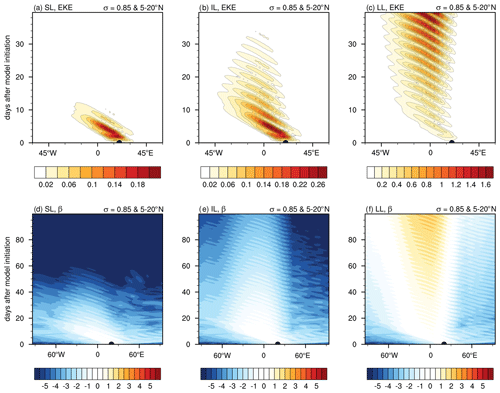
Figure 10Hovmöller diagram of EKE (a–c) and β (d–f) at σ=0.65 resulting from fixed heating on the short- (a, d), intermediate- (b, e), and long-lived (c, f) composite basic states averaged over 5–20∘ N. The black dot represents the location of the initial heating perturbation.
Another illustration of the behavior of the wave packets in the three simulations is presented in Fig. 11. Here, the streamfunction (σ=0.65 level), averaged over 10–20∘ N, is plotted against longitude for selected times. Note the different ranges for the ordinate in the three panels. Taken together with Fig. 10, it is evident that the wave packet in all three simulations remains nearly stationary. In the short- and intermediate-lived cases, the leading and lagging edges of the AEW packet slowly seem to be collapsing towards 0∘ E. They resemble the conceptual diagram for damped absolute instability shown in Fig. 2c. On the other hand, the amplification and expansion of the wave packet in the long-lived case resemble the conceptual diagram for absolute instability shown in Fig. 2a.
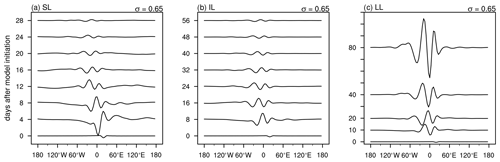
Figure 11Streamfunction (105 m2 s−1) averaged over 10–20∘ N at σ=0.65 and plotted as a function of longitude for selected days for short- (a), intermediate- (b), and long-lived (c) simulations. Each day's streamfunction is offset along the ordinate for visualization.
Figure 12 shows the global averaged EKE and its growth rate, with the latter defined as
In each simulation, the transient response to the fixed-heating forcing causes an initial spike in EKE, followed by a period of adjustment after the heating is switched off. As expected, the short- and intermediate-lived wave packet growth rates are negative owing to the stabilization effect of the imposed friction. The long-lived case shows exponential growth. It appears that 20 d of simulations is sufficient to reach this steady growth rate and signifies the emergence of the dominant normal mode for the localized jet.
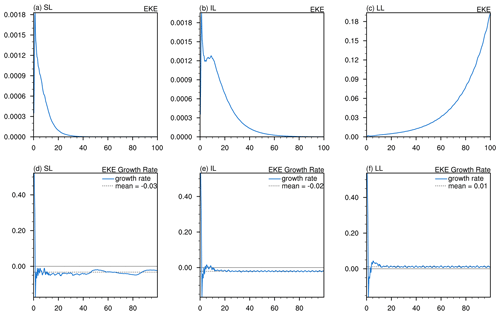
Figure 12Time series of the globally averaged EKE (a–c, J kg−1) and growth rates (d–f, d−1) resulting from the fixed-heating anomaly on the short- (a, d), intermediate- (b, e), and long-lived (c, f) basic states. The mean growth rate, averaged over the last 50 d of the simulation, is shown by the dashed line.
4.3 Group speed
Diaz and Aiyyer (2015) adapted the method of Orlanski and Chang (1993) to calculate the group speed across their simulated wave packets. We write it for the zonal group speed as follows:
where ua is the perturbation zonal ageostrophic wind, p is pressure, A is the area, Φ′ is the perturbation geopotential, is the basic state zonal wind, and Te is the total eddy energy, which was defined by Orlanski and Katzfey (1991) as the sum of the eddy kinetic energy and the eddy available potential energy:
where v is the perturbation velocity, αm is the time mean specific density, Θ is the potential temperature, is its horizontal average, and θ is the perturbation potential temperature. As written above, Cg includes the contribution of both the ageostrophic geopotential flux and the energy transport by the background flow.
To apply Eq. (9) to our model output, we integrate over latitudes 5∘ S–30∘ N in the meridional direction, half-wavelengths in the zonal direction, and the entire depth of the model in the vertical direction. The group speed is further averaged over days 30–35 for display. Figure 13 shows the calculation for the climatological and the three ensemble-averaged basic states. In all four cases, the group speed is westward on the leading edge, eastward on the lagging edge, and vanishes somewhere in between. For the short-lived case this happens at 30∘ W, for the intermediate-lived case around 10∘ W, and for the long-lived case around 0∘ E. Owing to upstream and downstream dispersion, portions of the wave packet remain within the region of instability. Thus, the condition for inviscid absolute instability for easterly mean flow (Eq. 4) is satisfied in all four ensemble-averaged basic states. The inclusion of damping stabilizes three of them. However, in light of our earlier discussion regarding the destabilizing role of moist convection and SMD, the wave packet's group dynamic provides a means for a persistent structure and amplification that can overcome damping via coupling with these additional energy sources.
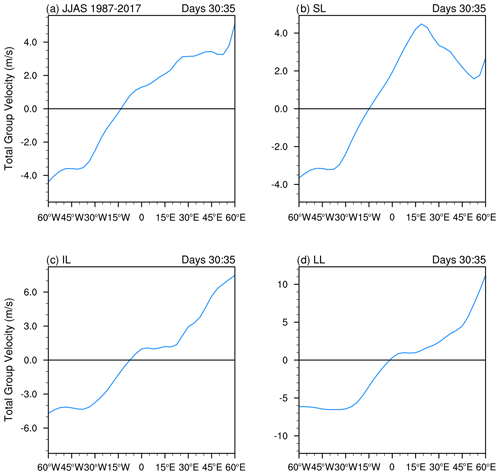
Figure 13Total group velocity (m s−1) averaged over days 30–35 of the simulation for the four basic states as marked on the panel: (a) the JJAS long-term climatology, (b) short-lived (SL), (c) intermediate-lived (IL), and (d) long-lived (LL). Cg is evaluated from Eq. (9), integrated over half-wavelengths in the zonal direction, from −5 to 30∘ N meridionally, throughout the model depth in the vertical direction.
4.4 Sensitivity to sponge region
The simulation for the long-lived case shows an exponentially growing stationary wave packet. Since the model is global, and allows for reentry of waves, it is of interest to examine whether this affects the growth rate. A standard approach to minimizing re-entrant waves is to include a sponge region of damping (e.g., Dunkerton, 1993). We repeat our simulation for the long-lived case by imposing additional damping outside 60∘ W–60∘ E. The growth rate and the structure of the wave packets for this simulation are shown in Fig. 14. A comparison with Figs. 11 and 13 shows that the outcome, with and without the sponge region, is similar. This result provides confidence that the wave packet response and amplification are not dependent on reentering waves. It also points to the possibility of the existence of a mode that is characterized by local absolute instability. The evidence that we have provided for absolute instability is, however, circumstantial. A rigorous analysis (e.g., Pierrehumbert, 1984; Dunkerton, 1993) is needed to confirm its applicability.
4.5 Examples of convective wave packets
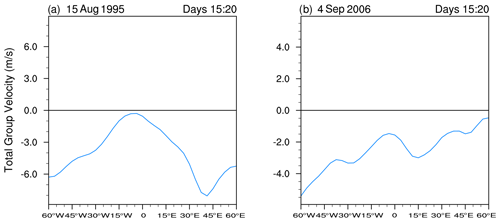
When we examine each of the 775 simulations individually, we find that the majority of them satisfy the criterion for inviscid absolute instability as given in Eq. (4). However, most of them are stabilized by damping and fall under the short-lived category. Only 22 cases satisfy the criterion for inviscid convective instability with westward group speed over the entire wave packet. We now briefly show two examples: one for the basic state taken from the 15 d average centered on 15 August 1995 and the other on 4 September 2006. The perturbation streamfunction (σ=0.65 level) for these two simulations is shown in Fig. 15. In both cases, the resulting wave packet after 5 d looks quite similar to the short-lived composite case. However, over time, the wave packet slowly moves beyond the coast of West Africa and is damped.
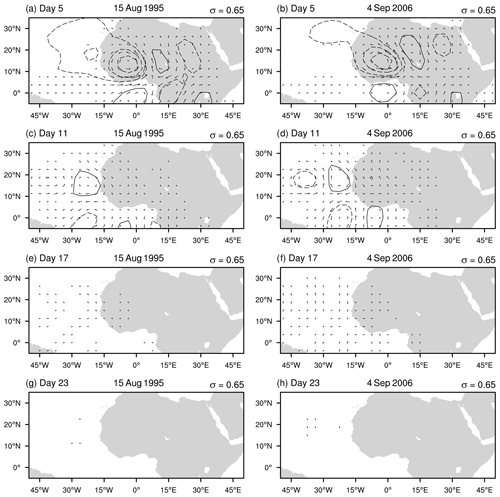
Figure 15Streamfunction (interval 1×105 m2 s−1 with negative values dashed) showing the wave response within the basic state formed by the 15 d average centered around 15 August 1995 (a, c, e, g) and 4 September 2006 (b, d, f, h).
The growth rates for these two cases are similar to the short-lived basic state simulations (not shown). The Hovmöller diagrams for EKE and the β parameter look similar to the short-lived case (not shown). However, the total group velocity (Fig. 16) shows uniformly negative values. This indicates that the entire wave packet propagates downstream. Note that we average the group velocity over days 15–20 in this case because the wave packet is mostly advected out of the region of instability after this period. In the absence of damping, the wave packet would experience growth as long as it remains within the area of instability. Once it exits the region, it will cease to experience growth. However, as seen in Fig. 15, the presence of damping stabilizes the wave packet, and it decays after initiation even while passing through the unstable region associated with the AEJ.
The objective of this work is to examine some characteristics of wave packets generated within the AEJ. In part, it is motivated by previous studies that have questioned the ability of the zonally localized AEJ to support growing AEWs (e.g., Thorncroft et al., 2008; Leroux and Hall, 2009). Our work is guided by two hypotheses that we test using an idealized model.
Following the method used by Thorncroft et al. (2008) and Leroux and Hall (2009), we examine the response to transient heating within the AEW storm track using an idealized general circulation model. We begin with a climatological basic state and then a series of 15 d average states. Out of the 775 simulations, 67 % of the wave packets are short-lived, 17 % are intermediate-lived, and 15 % were long-lived. The basic states for these categories are further combined to yield ensemble-averaged states and three additional simulations are performed. In all three simulations, a nearly stationary wave packet ensues and is located over West Africa. The short- and intermediate-lived wave packets are eventually damped, but the long-lived wave packets remain unstable. The group velocity for these three wave packets, and indeed most of the basic states considered here, is found to be westward on the leading edge and eastward on the lagging edge of the wave packet. Only 22 cases showed uniformly westward group velocity across the wave packet.
All ensemble-averaged basic states considered here are associated with reversal in PV gradients and thus satisfy the criterion for inviscid barotropic–baroclinic instability. Consistent with that, the wave structures exhibit upshear tilt in horizontal and vertical planes. As expected, both barotropic and baroclinic conversions of energy from the basic state to the waves are found (not shown). The scope of the present work does not include a detailed examination of the differences in the basic state to account for the wave packet behavior. Nonetheless, we note that the long-lived basic state had more vertical and horizontal shear associated with the AEJ as compared to the short-lived basic state. As seen in Fig. 6, the AEJ in the long-lived basic state is stronger and is more directly located above the surface monsoon westerlies. This corresponds to stronger horizontal and vertical wind shear and, with increased barotropic–baroclinic energy conversions, yields a higher growth rate of the long-lived wave packet (Fig. 12).
We used the same experimental method as Thorncroft et al. (2008) and Leroux and Hall (2009) in order to maintain consistency and connections with previous related studies. The fact that the majority of basic states appear to be stabilized by the imposed damping agrees with Hall et al. (2006) and Leroux and Hall (2009). In the absence of spontaneous generation of AEWs, large amplitude external triggers may be necessary as proposed by Thorncroft et al. (2008). However, as noted in Sect. 1.2, recent work has shown that even a sub-critical AEJ may be destabilized by dust aerosol radiative effect (Nathan et al., 2017) and that moist convection has a major impact in maintaining and amplifying AEWs (Russell et al., 2020). Even triggered waves will fail to amplify if additional sources of destabilization are not present. Indeed, Thorncroft et al. (2008) found that the waves in their simulation were much weaker compared to observations even though the external forcing was of reasonable strength. They recognized that the triggered waves need to be coupled with moist convection in order to match the observed amplitudes in nature. While we have not accounted for interaction with precipitating moist convection and dust aerosol forcing, several other studies have documented their role in destabilizing AEWs (Berry and Thorncroft, 2012a; Schwendike and Jones, 2010; Janiga and Thorncroft, 2014; Poan et al., 2014; Grogan et al., 2016; Tomassini et al., 2017; Nathan et al., 2017; Russell and Aiyyer, 2020; Russell et al., 2020).
Returning to our motivating hypotheses and questions, our results suggest that the background flow over West Africa supports near-stationary wave packets. Furthermore, wave packet diagnostics indicate that the heuristic condition for inviscid absolute instability (e.g., Orlanski and Chang, 1993; Diaz and Aiyyer, 2015) is satisfied. This is the case not only for the climatological state but also for the majority of individual basic states from June–September 1987–2017. Most of our simulations produce only short-lived AEW packets, indicating that damping (in the absence of dust radiative or moist convective feedbacks) can stabilize an otherwise super-critical jet. Occasionally, however, the amplification via hydrodynamic instability does overcome damping and leads to exponential growth. Importantly, in nearly all cases, the wave packet remains within the area of instability over West Africa, thereby increasing the potential for interaction with moist convection and dust aerosols that are ubiquitous here.
Our results do not discount the role of large amplitude triggers of local or remote origin. If these externally forced disturbances project onto the AEW modes, they can lead to subsequent amplification if coupled with moist convection and dust radiative feedback. Our results suggest a complementary mechanism for AEW origin that relies on upstream energy dispersion. If we take the view that the group dynamic of AEWs favors a near-stationary wave packet within the AEJ, then the barotropic–baroclinic energy conversions associated with the jet, moist convection, and dust radiative effects can lead to rapid amplification. The potential for the AEJ to be absolutely unstable despite the damping – as noted for a subset of the basic states – also raises the possibility that AEW packets can be generated spontaneously within the AEJ and persist for multiple wave periods until nonlinear effects become prominent. The key result is that, whether the packet is triggered by an external forcing or generated internally, it is not swept out of the region of instability. This addresses the criticism that the limited zonal extent of the AEJ may be an impediment to AEW growth.
Our second hypothesis that intermittent activity of AEWs may be mediated by transition between convective and absolute instability of the basic states is not supported by the results. We find that convective wave packets are relatively infrequent in our simulations. It may be a limitation of our modeling framework, but nonetheless the implication is that the intermittent nature of AEW activity is likely set externally. Equatorial Kelvin waves and the Madden–Julian Oscillation have been shown to modulate AEW activity (e.g., Matthews, 2004; Leroux and Hall, 2009; Ventrice et al., 2011; Alaka and Maloney, 2012, 2014). These external intraseasonal oscillations can modify the background thermodynamic profile and lead to episodes of enhanced and suppressed AEW activity by altering the AEW growth rates.
While our direct numerical simulations suggest the potential applicability of absolute instability, our evidence must be considered circumstantial. A formal investigation of the spatial instability of the AEJ is warranted. A caveat of our findings is that we use a highly simplified representation of the atmosphere and neglect the feedback with precipitating moist convection and dust radiative feedback on the dynamics of the wave packets. It is likely that they may play an important role in modifying the nature of spatial instability of AEW packets. This remains to be explored further. In addition, our simulations do not represent modulation of AEWs by external phenomena such as the Madden–Julian Oscillation, convectively coupled Kelvin waves, or breaking extratropical baroclinic waves. The impact of these externally imposed sources of wave forcing on the group dynamics of AEWs also needs to be examined.
We find that the background flow over North Africa supports an upstream and downstream dispersing wave packet that is located within the AEJ. The implication is that, no matter what the source of the initial perturbations may be – spontaneous development or external triggers – the wave packet is not swept out of the localized region of instability. Consequently, AEWs have the opportunity to develop further via energy conversions from the jet and destabilization by moist convection and dust radiative forcing as shown in previous studies. Our work has shown the importance of the group propagation dynamic for the instability of AEWs.
The code for the University of Reading IGCM can be obtained from http://www.met.reading.ac.uk/~mike/dyn_models/igcm/ (last access: 20 March 2021) (University of Reading, 2021).
The reanalysis data used here can be obtained from the European Centre for Medium-Range Weather Forecasts (ECMWF; https://www.ecmwf.int/en/forecasts/datasets/reanalysis-datasets/era-interim/, last access: 20 March 2021) (ECMWF, 2021). The data documentation is provided in Dee et al. (2011).
JW conducted the simulations and analysis and produced the visualizations. AA performed some of the analysis and conducted the sponge region experiments. JW and AA wrote computer code for analysis and visualization, and both wrote the text of the paper.
The authors declare that they have no conflict of interest.
We thank Walter Robinson, Carl Schreck, Arlene Laing, Stu Bishop, James Russell, and Ademe Mekonnen for useful discussions. The original code for the model used here was kindly provided by Nick Hall. We are also grateful to three anonymous reviewers for their numerous constructive comments.
This work was supported by US National Science Foundation (NSF) through award no. 1433763.
This paper was edited by Peter Knippertz and reviewed by three anonymous referees.
Aiyyer, A., Mekonnen, A., and Schreck III, C. J.: Projection of Tropical Cyclones on Wavenumber-Frequency-Filtered Equatorial Waves, J. Climate, 25, 3653–3658, https://doi.org/10.1175/JCLI-D-11-00451.1, 2012. a
Alaka, G. J. and Maloney, E. D.: The Influence of the MJO on Upstream Precursors to African Easterly Waves, J. Climate, 25, 3219–3236, https://doi.org/10.1175/JCLI-D-11-00232.1, 2012. a, b, c
Alaka, G. J. and Maloney, E. D.: The Intraseasonal Variability of African Easterly Wave Energetics, J. Climate, 27, 6559–6580, https://doi.org/10.1175/JCLI-D-14-00146.1, 2014. a, b, c
Berry, G. J. and Thorncroft, C. D.: African Easterly Wave Dynamics in a Mesoscale Numerical Model: The Upscale Role of Convection, J. Atmos. Sci., 69, 1267–1283, 2012a. a
Berry, G. J. and Thorncroft, C. D.: African Easterly Wave Dynamics in a Mesoscale Numerical Model: The Upscale Role of Convection, J. Atmos. Sci., 69, 1267–1283, https://doi.org/10.1175/JAS-D-11-099.1, 2012b. a
Briggs, R. J.: Electron-Stream Interaction with Plasmas, MIT Press, MIT Press, Cambridge, MA, available at: https://direct.mit.edu/books/book/4332/Electron-Stream-Interaction-with-Plasmas (last access: 20 March 2021), 1964. a
Burpee, R. W.: The Origin and Structure of Easterly Waves in the Lower Troposphere of North Africa, J. Atmos. Sci., 29, 77–90, 1972. a
Chang, E. K. M., Lee, S., and Swanson, K. L.: Storm Track Dynamics, J. Climate, 15, 2163–2183, https://doi.org/10.1175/1520-0442(2002)015<02163:STD>2.0.CO;2, 2002. a
Charney, J. G. and Stern, M. E.: On the Stability of Internal Baroclinic Jets in a Rotating Atmosphere, J. Atmos. Sci., 19, 159–172, 1962. a
Dee, D. P., Uppala, S. M., Simmons, A. J., Berrisford, P., Poli, P., Kobayashi, S., Andrae, U., Balmaseda, M. A., Balsamo, G., Bauer, P., Bechtold, P., Beljaars, A. C. M., van de Berg, L., Bidlot, J., Bormann, N., Delsol, C., Dragani, R., Fuentes, M., Geer, A. J., Haimberger, L., Healy, S. B., Hersbach, H., Hólm, E. V., Isaksen, L., Kållberg, P., Köhler, M., Matricardi, M., McNally, A. P., Monge-Sanz, B. M., Morcrette, J.-J., Park, B.-K., Peubey, C., de Rosnay, P., Tavolato, C., Thépaut, J.-N., and Vitart, F.: The ERA-Interim Reanalysis: Configuration and Performance of the Data Assimilation System, Q. J. Roy. Meteorol. Soc., 137, 553–597, 2011. a
Diaz, M. and Aiyyer, A.: Energy Dispersion in African Easterly Waves, J. Atmos. Sci., 70, 130–145, 2013a. a, b, c
Diaz, M. and Aiyyer, A.: The Genesis of African Easterly Waves by Upstream Development, J. Atmos. Sci., 70, 3492–3512, 2013b. a
Diaz, M. and Aiyyer, A.: Absolute and Convective Instability of the African Easterly Jet, J. Atmos. Sci., 72, 1805–1826, 2015. a, b, c, d, e, f, g, h, i
Dickinson, M. and Molinari, J.: Climatology of Sign Reversals of the Meridional Potential Vorticity Gradient over Africa and Australia, Mon. Weather Rev., 128, 3890–3900, https://doi.org/10.1175/1520-0493(2001)129<3890:COSROT>2.0.CO;2, 2000. a
Dunkerton, T. J.: Inertial Instability of Nonparallel Flow on an Equatorial β-Plane, J. Atmos. Sci., 50, 2744–2758, https://doi.org/10.1175/1520-0469(1993)050<2744:IIONFO>2.0.CO;2, 1993. a, b, c, d
ECMWF – European Centre for Medium-Range Weather Forecasts: ERA-Interim, available at: https://www.ecmwf.int/en/forecasts/datasets/reanalysis-datasets/era-interim/, last access: 20 March 2021. a
Fink, A. H. and Reiner, A.: Spatiotemporal Variability of the Relation Between African Easterly Waves and West African Squall Lines in 1998 and 1999, J. Geophys. Res., 108, 1–17, 2003. a
Grogan, D. F. P., Nathan, T. R., and Chen, S. H.: Effects of Saharan Dust on the Linear Dynamics of African Easterly Waves, J. Atmos. Sci., 73, 891–911, 2016. a, b
Hall, N. M. J. and Sardeshmukh, P. D.: Is the Time-Mean Northern Hemisphere Flow Baroclinically Unstable?, J. Atmos. Sci., 55, 41–56, https://doi.org/10.1175/1520-0469(1998)055<0041:ITTMNH>2.0.CO;2, 1998. a
Hall, N. M. J., Kiladis, G. N., and Thorncroft, C. D.: Three-Dimensional Structure and Dynamics of African Easterly Waves. Part II: Dynamical Modes, J. Atmos. Sci., 63, 2231–2245, 2006. a, b, c, d, e, f, g, h, i, j
Hsieh, J.-S. and Cook, K. H.: Generation of African Easterly Wave Disturbances: Relationship to the African Easterly Jet, Mon. Weather Rev., 133, 1311–1327, 2005. a
Hsieh, J.-S. and Cook, K. H.: A study of the energetics of African easterly waves using a regional climate model, J. Atmos. Sci., 64, 421–440, https://doi.org/10.1175/JAS3851.1, 2007. a
Hsieh, J.-S. and Cook, K.: On the instability of the African easterly jet and the generation of African waves: Reversals of the potential vorticity gradient, J. Atmos. Sci., 65, 2130–2151, https://doi.org/10.1175/2007JAS2552.1, 2008. a
Huerre, P. and Monkewitz, P. A.: Local and Global Instabilities in Spatially Developing Flows, Annu. Rev. Fluid Mech., 22, 473–537, 1990. a
Janiga, M. A. and Thorncroft, C. D.: Convection over Tropical Africa and the East Atlantic during the West African Monsoon: Regional and Diurnal Variability, J. Climate, 27, 4159–4188, 2014. a, b
Jones, C., Mahowald, N., and Luo, C.: Observational evidence of African desert dust intensification of easterly waves, Geophys. Res. Lett., 31, L17208, https://doi.org/10.1029/2004GL020107, 2004. a
Kanamitsu, M., Ebisuzaki, W., Woollen, J., Yang, S.-K., Hnilo, J. J., Fiorino, M., and Potter, G. L.: NCEP-DOE AMIP-II Reanalysis (R-2), B. Am. Meteorol. Soc., 83, 1631–1644, 2002. a
Karyampudi, V. M. and Carlson, T. N.: Analysis and Numerical Simulations of the Saharan Air Layer and Its Effect on Easterly Wave Disturbances, J. Atmos. Sci., 45, 3102–3136, https://doi.org/10.1175/1520-0469(1988)045<3102:AANSOT>2.0.CO;2, 1988. a
Laing, A. G., Fritsch, J. M., and Negri, A. J.: Contribution of Mesoscale Convective Complexes to Rainfall in Sahelian Africa: Estimates from Geostationary Infrared and Passive Microwave Data, J. Appl. Meteorol., 38, 957–964, 1999. a
Laing, A. G., Carbone, R. E., and Levizzani, V.: Cycles and Propagation of Deep Convection over Equatorial Africa, Mon. Weather Rev., 139, 2832–2853, 2011. a
Leroux, S. and Hall, N. M. J.: On the Relationship between African Easterly Waves and the African Easterly Jet, J. Atmos. Sci., 66, 2303–2316, 2009. a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q
Leroux, S., Hall, N. M. J., and Kiladis, G. N.: A climatological study of transient-mean-flow interactions over West Africa, Q. J. Roy. Meteorol. Soc., 136, 397–410, https://doi.org/10.1002/qj.474, 2010. a
Leroux, S., Hall, N. M., and Kiladis, G. N.: Intermittent African Easterly Wave Activity in a Dry Atmospheric Model: Influence of the Extratropics, J. Climate, 24, 5378–5396, 2011. a, b
Ma, P.-L., Zhang, K., Shi, J. J., Matsui, T., and Arking, A.: Direct Radiative Effect of Mineral Dust on the Development of African Easterly Waves in Late Summer, 2003–07, J. Appl. Meteorol. Clim., 51, 2090–2104, https://doi.org/10.1175/JAMC-D-11-0215.1, 2012. a
Mak, M. and Cai, M.: Local Barotropic Instability, J. Atmos. Sci., 46, 3289–3311, https://doi.org/10.1175/1520-0469(1989)046<3289:LBI>2.0.CO;2, 1989. a
Mass, C.: A Linear Primitive Equation Model of African Wave Disturbances, J. Atmos. Sci., 36, 2075–2092, https://doi.org/10.1175/1520-0469(1979)036<2075:ALPEMO>2.0.CO;2, 1979. a
Matthews, A. J.: Intraseasonal Variability over Tropical Africa during Northern Summer, J. Climate, 17, 2427–2440, https://doi.org/10.1175/1520-0442(2004)017<2427:IVOTAD>2.0.CO;2, 2004. a, b, c
Mekonnen, A. and Rossow, W. B.: The Interaction Between Deep Convection and Easterly Waves over Tropical North Africa: A Weather State Perspective, J. Climate, 24, 4276–4294, https://doi.org/10.1175/2011JCLI3900.1, 2011. a
Nathan, T. R., Grogan, D. F. P., and Chen, S.-H.: Subcritical Destabilization of African Easterly Waves by Saharan Mineral Dust, J. Atmos. Sci., 74, 1039–1055, 2017. a, b, c
Norquist, D. C., Recker, E. E., and Reed, R. J.: The Energetics of African Wave Disturbances as observed During Phase III of GATE, Mon. Weather Rev., 105, 334–342, https://doi.org/10.1175/1520-0493(1977)105<0334:TEOAWD>2.0.CO;2, 1977. a, b
Orlanski, I. and Chang, E. K. M.: Ageostrophic Geopotential Fluxes in Downstream and Upstream Development of Baroclinic Waves, J. Atmos. Sci., 50, 212–225, 1993. a, b, c, d
Orlanski, I. and Katzfey, J.: The Life Cycle of a Cyclone Wave in the Southern Hemisphere Part I: Eddy Energy Budget, J. Atmos. Sci., 48, 1972–1997, 1991. a, b
Pierrehumbert, R. T.: Local and Global Baroclinic Instability of Zonally Varying Flow, J. Atmos. Sci., 41, 2141–2162, 1984. a, b, c, d, e
Poan, D. E., Lafore, J.-P., Roehrig, R., and Couvreux, F.: Internal processes within the African Easterly Wave system, Q. J. Roy. Meteorol. Soc., 141, 1121–1136, https://doi.org/10.1002/qj.2420, 2014. a
Reed, R. J., Norquist, D. C., and Recker, E. E.: The Structure and Properties of African Wave Disturbances as Observed During Phase III of GATE, Mon Weather Rev., 105, 317–333, 1977. a
Rennick, M. A.: Generation of African Waves, J. Atmos. Sci., 33, 1955–1969, 1976. a
Russell, J. O. H. and Aiyyer, A.: The Potential Vorticity Structure and Dynamics of African Easterly Waves, J. Atmos. Sc., 77, 871–890, https://doi.org/10.1175/JAS-D-19-0019.1, 2020. a, b
Russell, J. O. H., Aiyyer, A., and Dylan White, J.: African Easterly Wave Dynamics in Convection-Permitting Simulations: Rotational Stratiform Instability as a Conceptual Model, J. Adv. Model. Earth Syst., 12, e01706, https://doi.org/10.1029/2019MS001706, 2020. a, b, c
Schwendike, J. and Jones, S. C.: Convection in an African Easterly Wave over West Africa and the eastern Atlantic: A model case study of Helene (2006), Q. J. Roy. Meteorol. Soc., 136, 364–396, 2010. a, b
Simmons, A. J.: A Note on the Instability of the African Easterly Jet, J. Atmos. Sci., 34, 1670–1674, 1977. a
Swanson, K. L.: Storm Track Dynamics, in: The Global Circulation of the Atmosphere, edited by: Schneider, T. and Sobel, A. H., Princeton University Press, Princeton, 78–103, 2007. a
Thorncroft, C. D. and Hoskins, B. J.: An Idealized Study of African Easterly Waves. I: A Linear View, Q. J. Roy. Meteorol. Soc., 120, 953–982, 1994. a, b
Thorncroft, C. D., Hall, N. M. J., and Kiladis, G. N.: Three-Dimensional Structure and Dynamics of African Easterly Waves. Part III: Genesis, J. Atmos. Sci., 65, 3596–3607, 2008. a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r
Tomassini, L., Parker, D. J., Stirling, A., Bain, C., Senior, C., and Milton, S.: The interaction between moist diabatic processes and the atmospheric circulation in African Easterly Wave propagation, Q. J. Roy. Meteorol. Soc., 143, 3207–3227, 2017. a, b
University of Reading: Baroclinic Model, IGCM, Dynamical Processes Group Department of Meteorology, University of Reading, National Centre for Atmospheric Science, Reading, available at: http://www.met.reading.ac.uk/~mike/dyn_models/igcm/, last access: 20 March 2021. a
Ventrice, M. J., Thorncroft, C. D., and Roundy, P. E.: The Madden-Julian Oscillation's Influence on African Easterly Waves and Downstream Tropical Cyclogenesis, Mon. Weather Rev., 139, 2704–2722, https://doi.org/10.1175/MWR-D-10-05028.1, 2011. a, b, c