the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
The stratosphere: a review of the dynamics and variability
Neal Butchart
Large-scale, intra-seasonal to inter-annual variability of the stratosphere is reviewed. Much of the variability is dynamical and induced by waves emanating from the troposphere. It is largely characterized by fluctuations in the strength of the polar vortex in winter and a quasi-biennial oscillation in the equatorial winds. Existing theories for the variability are generally formulated in terms of wave–mean-flow interactions, with refinements due, in part, to teleconnections between the tropics and extratropics. Climate and seasonal forecast models are able to reproduce much of the observed polar stratospheric variability and are increasingly successful in the tropics too. Compared to the troposphere the models display longer predictability timescales for variations within the stratosphere. Despite containing just ∼17 % of the atmosphere's mass, the stratosphere's variability exerts a powerful downward influence on the troposphere that can affect surface extremes. The stratosphere is therefore a useful source of additional skill for surface predictions. However, a complete dynamical explanation for the downward coupling is yet to be established.
The works published in this journal are distributed under the Creative Commons Attribution 4.0 License. This license does not affect the Crown copyright work, which is re-usable under the Open Government Licence (OGL). The Creative Commons Attribution 4.0 License and the OGL are interoperable and do not conflict with, reduce or limit each other.
© Crown copyright 2022
The existence of the stratosphere, or at least a second layer to the Earth's atmosphere, was first established at the beginning of the twentieth century when Assmann (1902) and Teisserenc de Bort (1902) independently noted from balloon observations that from altitudes of 10–12 km up to around 17 km (the maximum achieved by the balloons) the atmosphere is isothermal, unlike lower down where the temperatures decrease with altitude. The term stratosphere1 from the French stratosphère meaning “sphere of layers” was introduced by Teisserenc de Bort (1902), who also gave us the term troposphere for the lowermost layer of the atmosphere. Nowadays it is recognized that the stratosphere is not isothermal and extends up to about 50 km with temperatures, in general, increasing with height (Fig. 1). Above that, temperatures decrease upward in the mesosphere before increasing upward again in the thermosphere (Fig. 1). These three layers, stratosphere, mesosphere and thermosphere, are often collectively referred to as the “middle atmosphere” (Andrews et al., 1987). They contain ∼17 % of the mass of the Earth's atmosphere, with the majority of that in the stratosphere (Baldwin et al., 2019). The focus of this review is the dynamics and dynamically driven variability of the stratosphere with some consideration given to how this influences the troposphere.
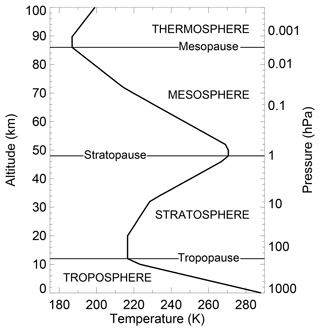
Figure 1Annually averaged mid-latitude temperature profile, based on the US Standard Atmosphere (Committee on Extension of Standard Atmosphere, 1976; Minzner, 1977).
The stratosphere is also the home of the ozone layer (McElroy and Fogal, 2008), which protects us from harmful ultraviolet (UV) radiation (Boucher, 2010). In order to explain some early ozone observations, Dobson et al. (1929) suggested the concept of a global-scale mass circulation which, with later refinements, evolved into what we now know as the Brewer–Dobson circulation (Butchart, 2014). This is a dynamically driven circulation (Sect. 2.2), and one consequence is that it drives the seasonal and zonally averaged temperatures of the extratropical stratosphere away from radiative equilibrium. Instead, on seasonal timescales and large spatial scales, the climate of the stratosphere can be described as being in radiative–dynamical equilibrium (Sect. 2.2).
A similar conceptual global transport circulation was invoked by Brewer (1949) to explain why the stratosphere was observed to be dry. With very low amounts of water vapour the dynamical effects of latent heating due to water experiencing phase transitions can be ignored in the stratosphere. Negligible latent heating effects and strong stable stratification due to the temperatures increasing with height distinguishes stratospheric dynamics from tropospheric dynamics which generally involve moist processes.
Variability in stratospheric winds and temperatures arises mostly through dynamical processes, though fluctuations in incoming solar radiation, temporary volcanic aerosol injections, and changes in composition such as ozone depletion and recovery also contribute variability on a range of timescales. This review considers only the large-scale variability of dynamical origins for which the two most distinctive phenomena are sudden stratospheric warmings (SSWs; Sect. 2.5), which occur in high latitudes in winter, mostly in the Northern Hemisphere (NH), and the quasi-biennial oscillation (QBO; Sect. 3.1) observed in the equatorial stratospheric winds. Comprehensive reviews of the QBO and SSWs can be found in the Baldwin et al. (2001, 2021, respectively) series of reviews.
The first recorded SSW was over Berlin in January 1952 when Scherhag (1952) measured a rise in stratospheric temperatures of ∼30 K in just 2 d. Measurements in following years showed that this was neither a one-off event nor local, with similar SSWs occurring roughly every other year in the boreal winter and the rapid increase in temperatures also seen in the zonal mean (Baldwin et al., 2021). Current theoretical understanding of SSWs originates from the pioneering research by Matsuno (1971) and relies on three principle dynamical mechanisms: propagation of Rossby waves from the troposphere, the waves interacting with the mean flow due to wave breaking and dissipation, and an induced mean meridional overturning circulation (Haynes et al., 1991) leading to rapid adiabatic warming (i.e. the SSW). These same dynamical mechanisms drive the extratropical stratosphere away from radiative balance and explain the observed latitudinally varying structures of the zonal mean temperature and wind fields (Sect. 2.2). Intraseasonal and interannual variability is, in turn, driven by variability in this dynamical forcing of the stratosphere away from radiative balance.
Tropical variability in the lower and middle stratosphere is dominated by the QBO, which, like SSWs, was discovered from observations that became available in the 1950s (Ebdon and Veryard, 1961; Reed et al., 1961). The QBO is one of the most distinctive modes of natural variability seen anywhere in the Earth's atmosphere that is not directly associated with the changing seasons. It is characterized by alternate layers of eastward and westward winds descending through the equatorial stratosphere roughly every 28 months. The original canonical model proposed to explain this oscillation (Lindzen and Holton, 1968; Holton and Lindzen, 1972) remains relevant today. Again this invokes vertical wave propagation from the troposphere and wave–mean-flow interactions, though now the waves are equatorial Kelvin and Rossby-gravity waves plus a broad spectrum of gravity waves (Sect. 3.1).
Despite waves from the troposphere being instrumental in most of the dynamical variability seen throughout the stratosphere, fluctuations in the wave flux from the troposphere are not essential to obtain the variability. Indeed, the QBO arises mostly from the feedback between the waves and the mean flow rather than an oscillation in the wave sources and filtering within the troposphere (Anstey et al., 2022b). Likewise, Hardiman et al. (2020) argue that, for monthly means, vacillations between the waves and mean flow can explain much of the sub-seasonal and interannual variability in the strength of the NH polar vortex. Teleconnections between the tropics and extratropics also feature in determining variability in the different regions with, for example, the strength of the NH polar vortex and likely occurrence of an SSW dependent on the phase of the QBO (Anstey and Shepherd, 2014). The reverse influence of the extratropics on the tropics was thought to be relatively weak (O'Sullivan, 1997) until two interruptions of the regular QBO cycles in recent years by waves from the extratropics (Newman et al., 2016; Osprey et al., 2016; Anstey et al., 2021) prompted a reassessment (Sect. 4.2).
Advances over the last two decades have established that variability in the stratosphere can exert a powerful downward influence on the troposphere both in the extratropics (Kidston et al., 2015) and the tropics (Haynes et al., 2021), as well as on a wide range of timescales. This has fundamentally changed the traditional view that the relatively small mass of the stratosphere restricts it to a passive or weak dynamical role in surface climate and weather. Instead it is now generally accepted that the dynamical coupling between the stratosphere and troposphere is two-way. Hence, a better understanding of stratospheric variability together with improvements in its representation in global models (Gerber et al., 2012; Anstey et al., 2022a) will potentially bring benefits of more reliable climate projections (Gerber and Manzini, 2016) and more accurate predictions of surface weather (Butler et al., 2016; Domeisen et al., 2020a) and extremes (Domeisen and Butler, 2020).
2.1 Zonal mean climate
Unlike the troposphere, the stratosphere does not feel the thermal inertia of the oceans and without dynamics would be close to radiative equilibrium at all latitudes with a thermal structure and underlying annual cycle determined by a balance between heating due to absorption of incoming radiation (mostly solar UV) and cooling due to infrared emissions (Shine, 1987). Maximum radiative heating occurs at the summer pole, while the maximum cooling is located at the winter pole. At the equinoxes the maximum heating shifts to the Equator with cooling at both poles. Consequently, the winter pole is relatively cold, while the summer pole is relatively warm. This leads to a meridional temperature gradient and, by gradient wind balance, an eastward2 circumpolar vortex in the winter hemisphere with westward flow in the summer hemisphere. These features are seen for the observed zonal mean stratospheric climate (Fig. 2), though there are significant departures from the radiatively determined state, particularly in winter (cf. Fig. 2 with Figs. 6 and 8 in Shine, 1987). During the polar night when there is no incoming solar radiation the observed high-latitude stratosphere is significantly warmer than would be expected if temperatures were determined by the radiative cooling alone, especially in the NH (Shine, 1987). Correspondingly, the eastward polar night jets are weaker than for the radiatively determined state with the NH jet peaking at just over 40 m s−1 in the upper stratosphere (Fig. 2a) compared to ∼100 m s−1 in the Southern Hemisphere (SH; Fig. 2b), which is also closer to the radiative equilibrium value (Shine, 1987).
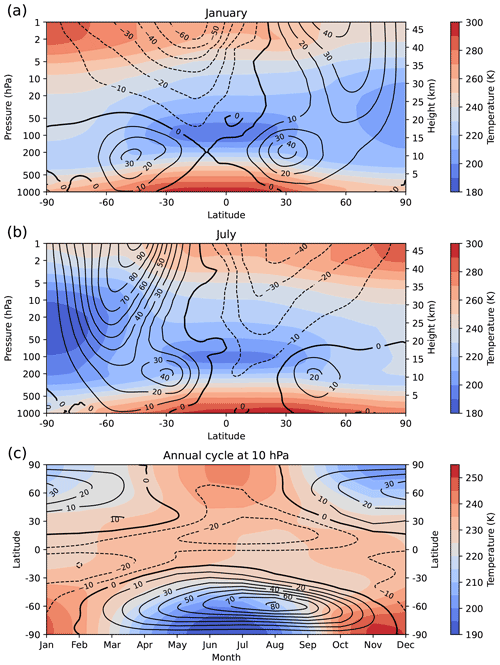
Figure 2Zonal and monthly mean 1979–2020 climatology based on 6-hourly ERA5.1 reanalyses data (Hersbach et al., 2020) for temperature (K; colour shading) and zonal winds (m s−1; black contours) for (a) January, (b) July and (c) the annual cycle at 10 hPa. The contour interval for the winds is 10 m s−1, with negative values indicated by dashed contours. Data kindly retrieved from the ERA5 archive and processed by Martin Andrews.
Inter-hemispheric differences are also visible in the annual cycle of the climatological temperatures and zonal wind at 10 hPa (Fig. 2c). The annual cycle amplitude is larger in the SH than the NH, and the transition from eastward to westward winds in the SH occurs 8 and not 6 months after the corresponding transition in the NH. Despite these differences the underlying annual cycle throughout the extratropical stratosphere is fundamentally a radiatively driven phenomenon with an amplitude comparable to the dynamically driven intraseasonal and interannual variability (see below).
The departure of the stratosphere from radiative equilibrium is due to a hemispheric-scale mean meridional overturning circulation, sometimes referred to as the “diabatic circulation”. It consists of (i) ascent at the tropical tropopause and throughout the tropical stratosphere and (ii) descent in the extratropical stratosphere causing adiabatic cooling and warming, respectively. Murgatroyd and Singleton (1961) were the first to attempt a calculation of this circulation, though a full theoretical understanding was not obtained until the 1970s (Sect. 2.2). Nonetheless, Murgatroyd and Singleton's 1961 qualitative description of the structure of the circulation agrees well with current understanding of stratospheric dynamics.
2.2 Wave–mean-flow dynamics
Concurrent with Murgatroyd and Singleton's 1961 calculations, Charney and Drazin (1961) deduced from theory that the upward propagation of Rossby waves into the stratosphere can only occur through zonal mean winds that are eastward relative to the wave phase speed, and then only if those winds are not too strong. Even when these conditions are met, all but the largest-scale waves are inhibited from propagating. The planetary-scale waves that can propagate are mainly forced by surface topography and land–sea contrasts (Held et al., 2002; Garfinkel et al., 2020b), with some additional forcing resulting from baroclinic processes (Tung and Lindzen, 1979; Boljka and Birner, 2020). Based on the observed climatological zonal mean zonal winds (Fig. 2a and b) this then explains why the circulation in the summer stratosphere is relatively zonal symmetric and why the deviations from zonal symmetry are larger in the NH winter than the SH winter. In general, the zonal asymmetries are dominated by the first and second zonal wave harmonics as illustrated by the example daily maps of geopotential height at 10 hPa shown in Fig. 3. Also noticeable in the figure is the absence of zonal asymmetries in summer (Fig. 3b and c) and the weaker wave amplitudes in the SH compared to the NH (cf. Fig. 3a and d), which is due to the difference in the surface topography and the land–sea contrast between the hemispheres.
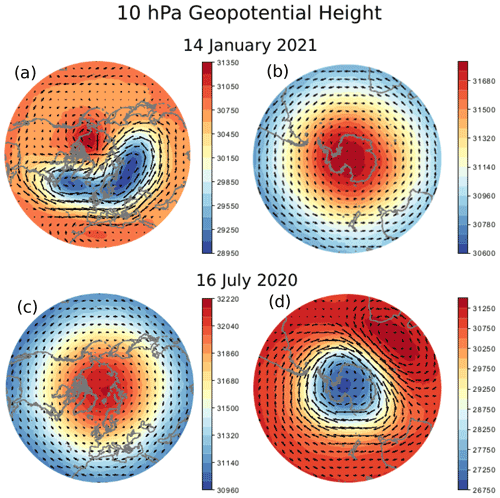
Figure 3Geopotential height (m) and vectors of horizontal wind (m s−1) at 10 hPa for (a) 14 January 2021 and (c) 16 July 2020 for the NH and (b) 14 January 2021 and (d) 16 July 2020 for the SH. From UK Met Office daily operational analysis for 12Z.
Charney and Drazin (1961) also showed that the steady, non-dissipated Rossby waves they considered had no effect on the mean flow. Similar theoretical relationships between mountain (gravity) waves and the mean flow were derived by Eliassen and Palm (1961) and form the basis for a non-acceleration theorem, or Eliassen–Palm theorem, which states that, to second order in wave amplitude, waves that are steady and conservative (i.e. waves that are not time varying and not subjected to any forcing or dissipation) do not change the mean flow. Following further theoretical developments in the 1960s and 1970s (e.g. Dickinson, 1968; Matsuno, 1971; Uryu, 1973, 1974; Boyd, 1976), Andrews and McIntyre (1976, 1978) introduced a generalized form of the Eliassen–Palm and Charney–Drazin theorems expressed in terms of the transformed Eulerian mean (TEM) equations, which are now widely used for analysing wave–mean-flow interactions (Sect. 8 in Held, 2019). The generalization of Andrews and McIntyre (1976, 1978) is ubiquitous as it is relevant to both gravity and Rossby waves and is applicable in the tropics as well as the extratropics.
Andrews and McIntyre (1976, 1978) derived the TEM equations by defining a residual mean meridional circulation,
and transforming the zonal mean thermodynamic and zonal momentum equations in latitude, log-pressure coordinates (ϕ, z) to
and
respectively. Here an overbar refers to a zonal average and a prime the deviation therefrom or eddy. Zonal, meridional and vertical velocities are denoted by u, v and w, respectively; θ is potential temperature; is the zonal mean diabatic (radiative) heating; is the basic state density with H defined as scale height for log-pressure coordinates, generally taken to be ∼7 km, and ρs is a sea level reference density. The rotation rate and radius of the Earth are Ω and a, respectively. On the right-hand side of Eq. (3) F is the Eliassen–Palm flux vector defined as
and
with
In the thermodynamic Eq. (2) the second term on the right-hand side can generally be neglected (Andrews and McIntyre, 1978) such that, for steady-state conditions, the equation is isomorphic to that used by Murgatroyd and Singleton (1961) to calculate the diabatic circulation. Dunkerton (1978) used this TEM equation to estimate the residual mean meridional circulation for steady conditions, and, as might be expected, his results agree remarkably well with those of Murgatroyd and Singleton (1961). From this Dunkerton (1978) deduced that, rather than the Eulerian mean meridional circulation , it is this residual mean circulation incorporating dynamical contributions from the eddy heat and momentum fluxes that is responsible for driving the stratosphere away from radiative equilibrium. Full theoretical details of the actual dynamical mechanisms involved are presented in the classic paper on downward control of the diabatic circulation by Haynes et al. (1991) and are not repeated here. One aspect that is worth noting is that the residual mean meridional circulation approximates Lagrangian transport and, on an hemispheric scale, forms the advective component of the Brewer–Dobson circulation, which also includes two-way mixing (Butchart, 2014).
For the TEM equations the non-acceleration relations derived by Eliassen and Palm (1961) reduce to the simple expression ; i.e. the forcing term on the right-hand side of the zonal momentum Eq. (3) is zero. F indicates the direction (Jucker, 2021) and magnitude of wave propagation in the meridional plane and, for small-amplitude waves, represents the flux of wave activity (Andrews, 1987). The observed climatological winter mean is negative throughout the stratosphere (Fig. 4) and therefore has a westward acceleration (eastward deceleration) effect on the circumpolar vortex. This explains why the polar night jets (Fig. 2a and b) are weaker than would be expected from purely radiative considerations (Sect. 2.1). The arrows in Fig. 4 indicate that Rossby waves are propagating upward from the troposphere, though on reaching the stratosphere they turn equatorward. Essentially this is because of the variation in latitude of the refractive index (due mainly to its dependence on the Coriolis parameter 2Ωsin ϕ) in the wave equation (Matsuno, 1970), which determines the direction of propagation of Rossby waves in the (ϕ,z) plane (Butchart et al., 1982). As expected, the wave fluxes are stronger in the northern winter than in the southern winter due to the relatively weak surface forcing in the SH.
Figure 4Climatological mean F (arrows) and (contours levels: , and ±8 m s−1 d−1, with dashed contours denoting negative values) for (a) December–February in the NH and (b) June–August in the SH, based on ERA-Interim (Dee et al., 2011) for the period of 1979–2018. Note the Equator is on the left in panels (a) and (b). For a clearer visualization of the direction of wave propagation F is scaled as , where p is pressure and ps is a reference sea level pressure taken as 1000 hPa. Figure is courtesy of Hua Lu. Figure 4a adapted with permission from Fig. 1b of Lu et al. (2015). © American Meteorological Society.
Rossby waves in the stratosphere are often transient and almost certainly thermally damped (Andrews et al., 1987), but the main cause of negative ∇⋅F and, therefore, an eastward deceleration (westward acceleration) of the mean flow is wave breaking, at least in the extratropics. Waves propagating vertically, which do not encounter a critical layer (i.e. where the phase speed approaches that of the mean flow and propagation is inhibited), attain large amplitudes due to the exponentially decreasing density with height, and the waves eventually break. Waves also break on encountering a critical layer either horizontally or vertically. Both gravity and Rossby waves experience amplitude growth with height. In the extratropical (and tropical) stratosphere, most gravity waves predominantly propagate upward3, with some reaching the mesosphere, where their breaking contributes significantly to driving the temperature away from radiative equilibrium (Leovy, 1964). On the other hand, as Rossby waves are mostly refracted equatorward before reaching the mesosphere (e.g. Fig. 4), the breaking occurs in the stratosphere and is now commonly diagnosed in terms of potential vorticity.
2.3 Potential vorticity
Like potential temperature (θ), potential vorticity (PV) is a quasi-conservative quantity in the stratosphere. With θ as the vertical coordinate,
where ζθ is the relative vorticity evaluated along isentropic surfaces (surfaces of constant θ) and g gravitational acceleration. In the stratosphere isentropic surfaces are quasi-horizontal. PV generally increases poleward due to the Coriolis parameter 2Ωsin ϕ in Eq. (7), and it is these gradients that support Rossby wave propagation. A key advance in our understanding came when McIntyre and Palmer (1983) presented coarse-grained maps of the isentropic distribution of PV derived from newly available satellite observations which showed that PV gradients in the middle stratosphere were not uniform at all latitudes. Instead they identified a “main vortex” with steep PV gradients at its edge surrounded by a “surf zone” exhibiting relatively weak large-scale gradients (Fig. 5). Today the main vortex is known as the “polar vortex”. McIntyre and Palmer (1983) argued that the tongues of PV seen drawn out from the main vortex in their maps (cf. Fig. 5b) gave the first “reasonably convincing direct view of the breaking of planetary scale Rossby waves”, and McIntyre and Palmer (1984) went on to claim these were, in fact, the “world’s largest breaking waves”.
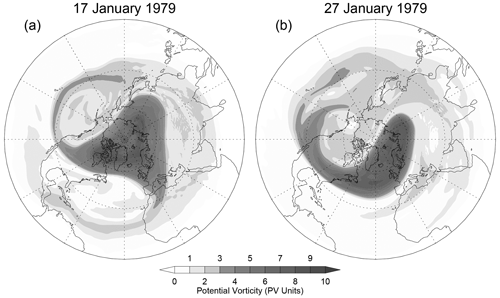
Figure 5Potential vorticity on the 850 K isentropic surface (∼10 hPa) for (a) 17 January and (b) 27 January 1979. Figure 2 from McIntyre and Palmer (1983) updated using PV derived from ERA-Interim (Dee et al., 2011) data. Note that in January 1979 observations of middle stratosphere were still rather sparse and therefore the extra detail in the updated maps is a manifestation of the reanalysis of the data.
PV maps provide a useful diagnostic for separating the reversible effects of Rossby wave propagation, such as the distortion and displacement of the polar vortex, from the irreversible effects of the waves breaking. The latter is characterized by tongues of PV drawn from the polar vortex (e.g. Fig. 5) and the eventual non-linear mixing of PV into the surf zone. A corollary of this is an erosion of the vortex with a sharpening of the PV gradients at its edge (Fig. 5). Therefore, both reversible and irreversible processes can contribute to the variability of the polar vortex.
McIntyre and Palmer (1983, 1984) conjectured that wave breaking and the concomitant vortex erosion occur almost continuously throughout the winter. By simply measuring the size of the vortex in terms of the area enclosed within contours of constant PV on the isentropic maps (Fig. 6a), Butchart and Remsberg (1986) confirmed this for the winter of 1978/79, with the confirmation subsequently extended to all northern winters from 1964–1982 by Baldwin and Holton (1988). Figure 6a shows that, with wave breaking, the vortex weakens throughout winter compared to what would be expected if there were no waves and the stratosphere evolved radiatively (Fig. 6b). If the amplitudes of the waves become sufficiently large, the vortex is displaced off the pole or even split in two, and usually this corresponds with the occurrence of an SSW (Sect. 2.5).
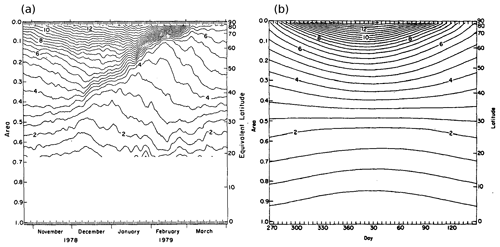
Figure 6Area enclosed by contours of potential vorticity on the 850 K isentropic surface (∼10 hPa) for (a) the 1978/79 NH winter and (b) an idealized simulation of the NH winter in the absence of Rossby waves. Figures 4 and 6 of Butchart and Remsberg (1986), respectively. Details of the calculations and information on the data used can be found in Butchart and Remsberg (1986). © American Meteorological Society. Used with permission.
2.4 Polar vortex variability
In terms of the interannual standard deviation of the monthly and zonal mean zonal winds, the maximum variability of the polar night jet occurs in high latitudes in the NH winter but in the SH winter is displaced toward mid-latitudes (Shiotani et al., 1993; Kuroda and Kodera, 2001) and does not extend down into the lower stratosphere (Fig. 7a and c, respectively). Instead the variability in the SH spring (Fig. 7d) is more similar to that of the NH winter, albeit slightly weaker, though stronger than the corresponding variability seen in the NH spring (Fig. 7b). This is what is expected for variability resulting from Rossby wave forcing from the troposphere. The mid-winter SH jet is generally strong enough (Fig. 2) to limit Rossby wave propagation (Sect. 2.2) and hence the variability, and the jet only becomes comparable in strength to the NH mid-winter jet as it weakens in spring (Fig. 2c). In contrast, by April in the NH the switch to the summer westward circulation has often already commenced (Fig. 2c), and, again, this inhibits Rossby wave propagation.
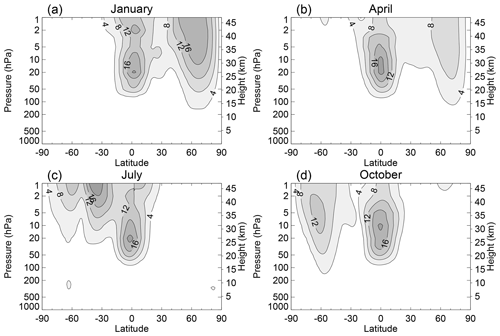
Figure 7Interannual standard deviation of monthly and zonal mean eastward wind (m s−1) for (a) January, (b) April, (c) July and (d) October. Based on the same ERA5.1 reanalysis data (Hersbach et al., 2020) for 1979–2020 as used in Fig. 2. The contour interval is 4 m s−1. The large interannual standard deviation in the low latitudes is a consequence of the QBO and is discussed further in Sect. 3.1.
An alternative approach for analysing the interannual variability of the polar night jets is to use empirical orthogonal functions (EOFs; Feser et al., 2000). For reanalysis data from 1980 to 1999 the first EOF explains 87 % of the variance in the zonal mean zonal wind at 50 hPa in the NH, while at the same level in the SH the first two EOFs explain 59 % and 35 % of the variance, respectively (Butchart et al., 2011). Variations in the jet strength are represented by the first mode of variability or EOF, while the second mode corresponds to a meridional shift of the jet. The two local maximums in the latitudinal structure of the interannual standard deviation for July (Fig. 7c) are then simply a manifestation of the larger contribution from the second EOF in the SH, as compared to the NH, which results from year-to-year fluctuations in the latitude of the jet maximum.
Because the strength of the polar night jet modulates Rossby wave propagation from the troposphere (Sect. 2.2, Charney and Drazin, 1961) there is potential for the jet strength to vacillate. A weakening followed by reversal of the eastward jet due to wave–mean-flow interactions diminishes wave propagation from the troposphere. This then reduces the deceleration effect of the waves, and radiative effects restore the jet's strength. More wave propagation is then allowed, and wave–mean-flow interactions begin to weaken the jet again; thus a vacillation cycle is created. Stratospheric vacillations of this form were first identified in idealized numerical experiments (Holton and Mass, 1976) and subsequently in a general circulation model (GCM) where they had a timescale of approximately 100 d (Christiansen, 1999). Establishing the role of vacillations in the observed variability is more challenging. Hardiman et al. (2020) found that for the 39 years of ERA-Interim (Dee et al., 2011) a single fixed-amplitude sine wave with a 120 d period provided a reasonable fit in the middle stratosphere (10 hPa, 55–65∘ N) to the sub-seasonal zonal wind variations from the mean seasonal cycle over the period November through March if a best-fit phase and constant offset were calculated for each of the 39 years. An important outstanding question is how much of the variability represented by the single sine wave is purely internal (i.e. would occur if the wave flux from the troposphere remained constant) and how much is the result of variations in the upward wave flux itself, at the tropopause (Scott, 2016)?
In contrast, Newman et al. (2001) concluded that the interannual variability of Arctic lower-stratospheric temperatures during spring is almost completely determined by the variability of the (meridional) eddy heat flux near the tropopause slightly earlier in the year. For large-scale Rossby waves the heat flux , where T is temperature) is approximately proportional to the vertical component of the EP flux (F(z), Eq. 5) and, hence, the vertical flux of wave activity. Over the 22 years of 1979–2001 Newman et al. (2001) observed that mean temperatures poleward of 60∘ N at 50 hPa and averaged from 1 to 16 March were significantly correlated with the 45–75∘ N mean eddy heat flux at 100 hPa averaged from 15 January to 28 February. In particular, they found that a strong planetary wave eddy heat flux in the 100–400 hPa and 45–75∘ N region during January-February results in a warm March polar lower stratosphere, while a weak planetary wave eddy heat flux results in a cold March polar lower stratosphere. Newman et al. (2001) noted that their result is consistent with a theoretical framework based on linear wave propagation and also robust to the choice averaging periods and latitude ranges. A similar relationship exists between Antarctic lower-stratospheric temperatures in spring and the eddy heat flux emerging from the troposphere slightly earlier in the year, and for both hemispheres this relationship appears robust across a range of model simulations (Austin et al., 2003; Manzini et al., 2003; Eyring et al., 2006; Osprey et al., 2010).
During the extended winter season, temperatures and zonal winds at high latitudes in the middle stratosphere can vary quite significantly from day to day in both hemispheres, as well as from year to year. For example, when the standard deviations of the daily variations in mean temperature poleward of 60∘ N and zonal mean zonal wind at 60∘ N are calculated at 10 hPa for October to March for each winter and then averaged for the 41 winters from 1979/80 to 2019/20, the values are ∼7 K and ∼13 m s−1, respectively, and comparable to the inter-annual spread in daily values shown by the light grey shading in Fig. 8a and b.
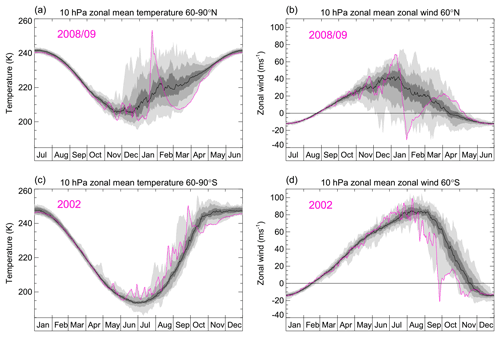
Figure 8Daily temperature and winds from MERRA2 data (Gelaro et al., 2017) for 1979–2020. The black line is the multi-year average of the daily time series with the 30th/70th and 10th/90th percentiles and the range shown by the dark, medium and light grey shading, respectively. The purple lines show the daily values for year 2008/09 in the NH and 2009 in the SH.
As noted above, the strongest inter-annual (and also daily) variability in the SH occurs roughly 2 months later in the annual cycle than in the NH. Therefore, the corresponding 6-month period in the SH is June to November, and for the 41 winters of 1980 to 2020 the averages of the standard deviations of the daily 10 hPa time series of the mean temperature poleward of 60∘ S and zonal mean zonal wind at 60∘ S are ∼4 K and ∼9 m s−1, respectively, which is slightly weaker than their NH counterparts. In both hemispheres daily variability is not uniform over the 6 months but includes periods when temperatures and winds evolve more steadily, similar to the summer months (Fig. 8) when the dynamical forcing is weak or nonexistent. At other times significant and rapid rises in temperature and deceleration of eastward polar night jet (e.g. purple curves in Fig. 8) are observed, especially in the NH. Corresponding rapid falls in temperature and/or a sudden acceleration of the jet are not observed as the upward-propagating Rossby waves can only decelerate the polar night jet (Sect. 2.2)4. Instead, a strengthening of the polar vortex and decline in the anomalously high polar temperatures occurs on the longer radiative damping timescales as illustrated by the behaviour seen in 2008/09 (Fig. 8a and b). Depending on the definition used, the events where there is a significant rapid rise in polar temperatures and a reversal from eastward to westward wind at 60∘ latitude, such as in January 2009 (e.g. Manney et al., 2009), are generally referred to as “sudden stratospheric warmings” (Butler and Gerber, 2018).
2.5 Sudden stratospheric warmings
In the decade following Scherhag's 1952 first observation of a mid-winter stratospheric warming (see Introduction), many more reports of anomalous warming events appeared in the literature (e.g. Keegan, 1962; Scherhag, 1960; Craig and Hering, 1959; Palmer, 1959; Teweles, 1958; Teweles and Finger, 1958), and by the early 1960s such events had acquired the name “stratospheric sudden warmings” (Reed et al., 1963), though today it is considered more appropriate to refer to these events as “sudden stratospheric warmings” (Butler et al., 2015). Initially SSWs were simply categorized as either mid-winter warmings or final warmings which are a manifestation of the year-to-year variability in the timing and vertical structure of the spring transition from an eastward to westward circulation in the middle- and high-latitude stratosphere (Matthias et al., 2021). In the 1960s warmings were further separated into “minor” and “major” (Butler et al., 2015). “Minor” warmings occur when a significant temperature increase is observed (i.e. at least 25 K in a period of a week or less) at any stratospheric level in any area of the wintertime hemisphere but the criteria for a major warming are not met. A warming is “major” if at 10 hPa or below the latitudinal mean temperature increases poleward from 60∘ latitude and an associated circulation reversal is observed (i.e. mean eastward winds poleward of 60∘ latitude are succeeded by mean westward winds in the same area). These criteria for distinguishing major from minor warmings are still used today, and the occurrences of major warmings can be identified in Fig. 8b and d as the times when the zonal winds fall below the zero wind line in the figures. This occurs only once in the SH (in 2002); i.e. only one major warming has been observed in the SH since 1979 and indeed since records began5. For any particular date during the NH winter the lightest grey shading in Fig. 8b shows that there are westward winds in less than 10 % of the years but, as SSWs can occur at any time during winter, major warmings are actually observed roughly every other year (Baldwin et al., 2021), though the exact frequency of occurrences varies from decade to decade (Domeisen, 2019) for reasons that are not yet fully understood.
Early research into understanding SSWs contributed to the development of the TEM theory of wave–mean-flow interactions (Sect. 2.2), and it is now accepted that the weakening and reversal of the polar night jet that occurs during warmings results from anomalously large negative values of ∇⋅F in Eq. (3). This generally results from an amplification and a refraction of upward-propagating Rossby waves poleward, where they deposit westward wave momentum mainly due to non-linear wave breaking (Sect. 2.3). A ramification of the non-zero ∇⋅F is an induced residual mean meridional circulation (Haynes et al., 1991) with adiabatic descent producing the observed warming of the polar stratosphere. Matsuno (1971) was the first to propose a model for SSWs based on planetary waves propagating from the troposphere, and in this model SSWs are classified as either (zonal) wave number one or wave number two warmings depending on which is the most dominant wave (O'Neill and Taylor, 1979). Higher wave number warmings do not occur as only the largest-scale Rossby waves can propagate up into stratosphere as a result of the Charney and Drazin (1961) theorem (Sect. 2.2). This then provides a dynamical distinction between major and minor warmings as the reversal of the flow at 10 hPa prohibits upward wave propagation beyond that level following a major warming. Consequently, after a major warming, the strong radiative cooling causes the polar temperatures to fall, though at a slower rate than the preceding rise, and SSWs are often followed by a period when the polar vortex is relatively cold and quiescent (e.g. see the winter 2008/09 curves in Fig. 8a and b).
One aspect of the mechanism for SSWs that is less well understood is the cause of the amplification of the waves. The rarity of SH SSWs provides compelling evidence for the importance of the wave flux from the troposphere as the SH topography and land–sea contrast is unable to produce sufficiently strong planetary wave forcing for more frequent SSWs as observed in the NH. However, even in the NH, anomalously large upward wave fluxes compared to the climatological values shown, for instance, in Fig. 4 are essential for SSWs. Some studies have argued that the anomalous fluxes result from blocking (e.g. Quiroz, 1986; Martius et al., 2009) and/or other tropospheric precursor events (e.g. Taguchi and Hartmann, 2006; Cohen and Jones, 2011), while other studies have stressed the importance of the state of the stratosphere. One possibility originally proposed by Palmer (1981a) to explain the occurrence of the 1979 SSW is the stratosphere is preconditioned to favour enhanced upward propagation of Rossby and gravity waves (Albers and Birner, 2014; Hitchcock and Haynes, 2016). An alternative possibility, first suggested by Plumb (1981), is that internal wave–mean-flow feedbacks within the stratosphere lead to a resonant growth of Rossby wave amplitudes (Matthewman and Esler, 2011). Most likely both the state of stratosphere and tropospheric precursors are relevant for the generation of SSWs since it has been estimated that only about a third of SSWs are preceded by extreme anomalous upward planetary wave fluxes from the lower troposphere (Birner and Albers, 2017).
Despite the uncertainty over the precise mechanism for the generation of SSWs, the geometric vortex parameters associated with the warming are known to be important (Albers and Birner, 2014). Hence the traditional mathematical classification of SSWs in terms of the dominant wave number is often supplemented by more physically based classifications of SSWs linked to the morphology of the polar vortex as diagnosed from maps of the isentropic distribution of PV (Waugh, 1997). Charlton and Polvani (2007) were the first to use such an approach and classified SSWs as either “(vortex) displacement”, characterized by a clear shift of the polar vortex off the pole, or “(vortex) split”, when the polar vortex breaks into two separate vortices of comparable size. Examples of displaced and split warming events are shown in Fig. 9b and c, respectively. A simple relationship between the geometric vortex parameters and a Fourier decomposition of the fields does not exist (Waugh, 1997), but wave number one warmings generally result in a vortex displacement, and the presence of wave number two is essential for a split vortex. Classifying SSWs according to whether they are vortex-splitting or vortex-displacement events has proved useful for tracking the nature and timing of the surface impacts of SSWs (Hall et al., 2021a). Therefore, understanding the generation of SSWs is likely to lead to a better understanding of their surface effects (Sect. 6.3).
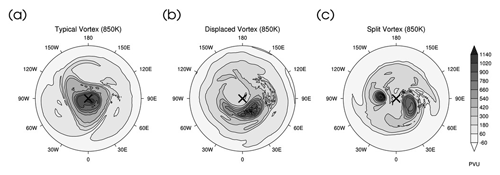
Figure 9Daily averaged PV (10−6 m2s−1 K kg−1) fields for three different states of the NH polar vortex on the 850 K isentropic surface: (a) the stable state of the vortex, (b) a displaced vortex and (c) a vortex that has split into two daughter vortices. Black crosses mark the North Pole. Figure 1 from Mitchell et al. (2011). © American Meteorological Society. Used with permission.
Modes of variability in the tropical stratosphere are associated with distinct peaks in spectral density, or power, in the periodogram of the monthly and zonal mean zonal winds at the Equator (Fig. 10, Pascoe et al., 2005). The first peak occurs at 6 months and represents the so-called “semi-annual oscillation (SAO)”, which is essentially a mesospheric phenomenon that extends down into the upper stratosphere. It is driven mainly by the transport of zonal momentum by vertically propagating equatorial and gravity waves plus cross-equatorial meridional advection of mean momentum which locks the SAO to the seasonal cycle (Kawatani et al., 2020).
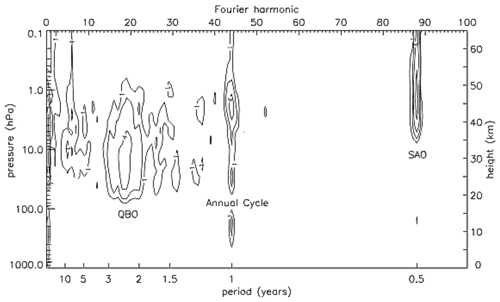
Figure 10Periodogram (Fourier analysis) of equatorial zonal mean zonal wind for 44 years of reanalysis data from 1958 to 2001. The Fourier harmonic axis indicates the number of cycles that a given periodic mode experienced during the 44 years. The periods of some Fourier harmonics are also indicated. Contours are drawn at Fourier amplitudes of 1, 2, 4, 8 and 16 m s−1. Figure 3 from Pascoe et al. (2005). © American Geophysical Union.
A second peak in the spectral density represents the annual cycle and is present throughout the depth of the stratosphere, though the amplitude of the cycle is much smaller than that for either the SAO in the upper stratosphere or the QBO (see below) in the lower and middle stratosphere, at least for the zonal mean zonal wind (Fig. 10). However, for the zonal mean temperature the annual cycle becomes the dominant mode at the tropical tropopause. It is driven by variations in adiabatic ascent (cooling) that result from the seasonal cycle in the diabatic (Brewer–Dobson) circulation (Yulaeva et al., 1994). As this seasonal cycle is a consequence of the inter-hemispheric differences in the wintertime extratropical wave driving (Sect. 2.2), the annual cycle in the tropical tropopause temperature is dynamically driven (e.g. Jucker and Gerber, 2017), in contrast to the annual cycle in the extratropical winds and temperature (Sect. 2.1), which is radiatively determined.
The third peak in the spectral density in the periodogram shown in Fig. 10 is broader than those for the SAO and annual cycle, thereby indicating a range of frequencies or periods – 22 to 40 months with an average of 28.5 months for the years 1958–2001 shown in the figure. It is also the dominant signal of variability in the equatorial zonal winds in the lower and middle stratosphere and results from the QBO.
3.1 Quasi-biennial oscillation
Ebdon and Veryard (1961) and Reed et al. (1961) are independently credited with the discovery of quasi-periodic reversals of the prevailing winds at the Equator from eastward to westward and back again roughly every 28 months in the lower and middle stratosphere. Corresponding oscillations were also identified in temperature and ozone, and soon after its discovery this irregular oscillation became known as the “quasi-biennial oscillation” or QBO (Angell and Korshover, 1964). The original discovery was based on single station data near the Equator, but similar behaviour is seen for the zonal means. For the zonal mean zonal wind, the signal is centred at the Equator with a latitudinal half width of about 12∘ (Baldwin et al., 2001). The most iconic image of the QBO is that of a Hovmöller diagram showing alternate descending layers of eastward and westward winds such as in Fig. 11. In this figure repeated transitions in monthly averaged zonal mean zonal winds at the Equator appear to originate in the upper stratosphere and then propagate downward, at least until 2016. These repeating irregular cycles have, in fact, been continuously observed since the 1950s before being unexpectedly interrupted in 2016 (Newman et al., 2016; Osprey et al., 2016). A second interruption was observed in 2019/20 in the zonal wind above Singapore (Anstey et al., 2021, Fig. 1a), though the occurrence of this interruption is not so apparent in the zonal mean zonal wind shown in Fig. 11.
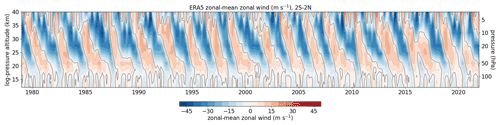
Figure 11Equatorial QBO. Hovmöller diagram of the vertical profile of the monthly averaged, zonal mean zonal wind, averaged from 2∘ S to 2∘ N. Based on ERA5 data (Hersbach et al., 2020) for the 1979–2021. Figure is courtesy of James Anstey.
In the years following its discovery, various dynamical mechanisms were proposed for the QBO, but it was difficult to explain key aspects such as (i) the QBO's downward propagation from 10 to 40 hPa without loss of amplitude and (ii) the super rotation of the atmosphere at the Equator during the eastward phase without vertical transport of momentum by equatorial waves. Lindzen and Holton (1968) were the first to consider such processes. They argued that with a broad spectrum of gravity waves propagating up from the troposphere there would be (i) eastward acceleration of the mean flow in regions of eastward vertical shear from the waves with eastward phase speeds and (ii) westward acceleration in regions of westward vertical shear from the waves with westward phase speeds. Moreover, since selective filtering by the mean flow meant that only waves with westward phase speeds could propagate through strong eastward winds, and vice versa for waves with eastward phase speeds, the shear zones would descend over time. This proposed mechanism was corroborated with results from idealized numerical experiments (Lindzen and Holton, 1968).
Instead of gravity waves, Holton and Lindzen (1972) considered vertical transport of momentum by thermally and mechanically damped upward-propagating planetary-scale Kelvin and Rossby-gravity waves and also obtained a realistic QBO in an idealized numerical model. However, subsequent studies suggest that the observed large-scale waves are unable to fully explain the observed QBO accelerations (Dunkerton, 1997). Most likely a combination of equatorial Kelvin and Rossby-gravity waves and small-scale gravity waves cause the alternating eastward and westward accelerations, though for the shear zones to descend, the wave forcings (accelerations) have to exceed the effects of mean upward advection by the residual mean meridional or diabatic circulation (Sect. 2.2), especially in the lower stratosphere (Match and Fueglistaler, 2020).
The two-way interaction between the mean flow and vertical fluxes of wave momentum is now well established as the fundamental process leading to the QBO, but major challenges remain in determining the details of the waves involved. Small-scale gravity waves are, in particular, difficult to observe (Hertzog, 2020), and hence the precise partitioning of the various wave types in the forcing of the QBO is uncertain. Estimating the wave momentum flux from the available observations is also problematic as it relies on numerous assumptions (Vincent and Alexander, 2020). In addition, the relative importance of the different wave dissipation mechanisms (e.g. damping or critical layer wave breaking that occurs when the phase speed is close to the wind speed) is poorly understood (Anstey et al., 2022b).
Strictly, the QBO is not a wave but a sequence of alternating eastward and westward wind regimes propagating downward. Therefore, the cycles are not pure sinusoids and display variability from cycle to cycle (Pascoe et al., 2005). Many cycles show the descent of the region of westward vertical shear apparently stalling around 30 hPa followed by the eastward winds persisting longer in the lower stratosphere (Fig. 11). Some of the variability most likely results from variations in the sources (mostly convection) of the tropical waves (Schirber, 2015), which are not well understood. Another possibility suggested by Dunkerton (1983) was that laterally propagating Rossby waves from the NH winter could modulate the strength of the QBO during its eastward phase, though evidence from idealized simulations (O'Sullivan, 1997) did not support this. Hence, prior to 2016, the consensus was the laterally propagating Rossby waves from the extratropics had only a small effect (e.g. Shuckburgh et al., 2001; Hamilton et al., 2004) on the QBO. Since 2016, horizontal wave momentum transport from the winter hemisphere has been implicated (Anstey et al., 2021) with initiating interruptions to the QBO cycling in 2016 and 2019, and this has prompted renewed interest in the role of the extratropics in modulating tropical stratospheric variability (see Sect. 4.2). A tendency for the phases of the QBO and annual cycle to align is thought to arise from the annual cycle in the tropical upwelling in the equatorial lower stratosphere that opposes the QBO's downward progression (Hampson and Haynes, 2004; Rajendran et al., 2018).
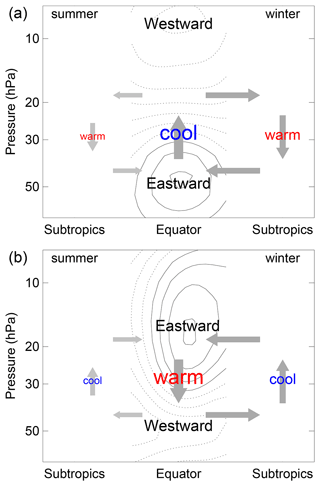
Figure 12Schematic showing the secondary residual meridional circulation (grey arrows) associated with the QBO equatorial temperature anomalies and the asymmetry in the circulation between the summer and winter hemispheres (Peña Ortiz et al., 2008). The locations of the warm and cool anomalies are shown in red and blue, respectively, with the font size giving a qualitative guide to the strength of the anomalies. Solid (dotted) contours indicate eastward (westward) zonal mean zonal winds at intervals of 10 m s−1 starting at ±5 m s−1 for (a) westward shear zone and (b) eastward shear zone. After Fig. 1 from Plumb and Bell (1982).
Due to thermal wind balance, a corresponding QBO signal is also observed in the temperatures at the Equator, with warm and cool anomalies where there is eastward and westward vertical wind shear, respectively (Baldwin et al., 2001). Maintaining the balance requires a secondary residual meridional circulation with ascent at the Equator in the regions of westward vertical shear and descent in regions of eastward vertical shear (Fig. 12). Plumb and Bell (1982) noted that vertical advection associated with this secondary circulation could account for some of the observed phase asymmetries by, for instance, retarding the downward propagation of the westward shear zone (cf. the stalling noted above) and speeding up the descent of the eastward shear zone. The secondary circulation also acts to concentrate the strongest eastward accelerations close to Equator (Dunkerton, 1991), which again is consistent with the observed meridionally narrower eastward phase compared to westward phase (Coy et al., 2016; Pahlavan et al., 2021a).
Vertical advection by the secondary circulation along with the QBO temperature anomalies is the primary reason for a similar period oscillation in ozone, which was first seen in subtropical data by Funk and Garnham (1962). At the Equator, transport (advection) is the dominant process in the lower stratosphere, and the ozone and wind QBO anomalies are generally in phase. Above about 15 hPa the effects of the temperature-dependent ozone chemistry becomes more relevant and the ozone anomalies change sign (Chipperfield et al., 1993). Feedbacks from these ozone anomalies, in turn, modulate the dynamical variability. For example, in model simulations ozone-related diabatic feedbacks prolong the QBO period and strengthen the QBO signal in temperature (Butchart et al., 2003) and zonal wind (Tian et al., 2006) in the lower and middle stratosphere. However, without a better understanding of the precise role of chemical processes in the ozone QBO, there is uncertainty in the strength of the feedbacks, and this remains an area of active research (Zhang et al., 2021).
One process providing a coupling between the tropics and extratropics in the stratosphere is the residual meridional circulation (Eq. 1). The extratropical planetary waves drive the diabatic circulation (Sect. 2.2), which is the principal reason for an annual cycle in temperature at the tropical tropopause. Likewise, the vertical component of the QBO's secondary meridional circulation causes adiabatic warming and cooling in the subtropical stratosphere and thereby forces a similar period oscillation in the temperatures in the region extending out to ∼45∘ latitude (Randel et al., 1999). In the subtropics the secondary circulation has descent (ascent) at altitudes where there is ascent (descent) at the Equator, and therefore the QBO anomaly in the temperature at the Equator changes sign poleward of about 15∘. This subtropical temperature QBO is mainly confined to the winter hemisphere due to a modulation by the seasonal cycle (Pahlavan et al., 2021a).
Other mechanisms through which the tropical variability, and in particular the QBO, has a remote impact on the extratropical stratosphere are less well understood (Anstey and Shepherd, 2014). These impacts also extend down into the troposphere (Sect. 6.3) and upward into the mesosphere and are commonly referred to as “QBO teleconnections” (Anstey et al., 2022b).
4.1 QBO teleconnections
Angell and Korshover (1964) provided the first evidence of the QBO possibly influencing the high-latitude stratosphere when they reported a QBO signal in polar temperatures (and ozone) in both hemispheres. With more years of observations (1962–1977) Holton and Tan (1980) found that the strength of the NH winter polar vortex correlated well with the phase of the equatorial QBO: a warmer, weaker vortex coincided with westward equatorial winds at 50 hPa, whereas when the winds were eastward the vortex was colder and stronger. A corollary of this so-called “Holton–Tan (HT) effect” first reported by Labitzke (1982) is that the occurrence of an SSW is more likely when the QBO winds are westward at 50 hPa than when the winds are eastward (Baldwin et al., 2021). Holton and Tan (1980) also noted a QBO signal in the SH zonal wind, this time in spring. An illustration of the HT effect in both hemispheres is presented in Fig. 13. Comparing this figure with the inter-annual standard deviation of the monthly mean zonal winds (Fig. 7) highlights the importance of QBO teleconnections in modulating the variability of the polar vortex.
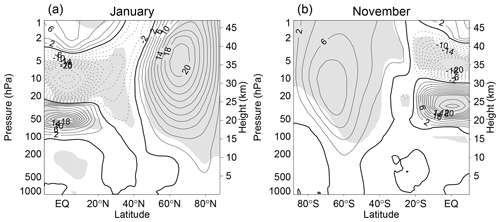
Figure 13Holton–Tan effect for January in the NH and November in the SH. Latitude–height cross sections of the monthly and zonal mean zonal wind averaged over all years when the winds at the Equator are ≥2.5 m s−1 minus the average over all years when the winds at the Equator are m s−1 at 50 and 30 hPa in January and November, respectively. The contour interval is 2 m s−1 for values between −20 and +20; otherwise, the interval is 10 m s−1. Negative values are shown by dotted contours, and shading indicates where the differences are statistically significant at the 95 % level according to Student's t test. Based on the same ERA5.1 reanalysis data (Hersbach et al., 2020) for 1979–2020 as used in Fig. 2.
A full understanding of the underlying mechanisms for the QBO polar vortex teleconnection remains elusive, despite numerous investigations into the HT effect following its discovery (Anstey and Shepherd, 2014). Holton and Tan (1980) noted that the zero zonal wind line at the edge of the tropical QBO was typically further poleward during the westward phase than in the eastward phase and argued that this contributed to confining the extratropical planetary waves more toward high latitudes, thereby leading to the warmer, weaker vortex. This is often referred to as the “Holton–Tan mechanism”. In contrast, Garfinkel et al. (2012) suggested that enhanced polar refraction of planetary waves results from the QBO's secondary meridional circulation modifying the Rossby wave refractive index in the subtropics. As the extratropical planetary wave activity is further modulated by the strength of the vortex (Sect. 2.4), this has, so far, hampered attempts to isolate which of these two proposed mechanisms for the HT effect is more relevant (Anstey et al., 2022b). More recently, Yamazaki et al. (2020) have suggested an alternative tropospheric pathway for the boreal winter in which a convection anomaly resulting from the QBO effect on the tropical troposphere (see Sect. 6.2) generates a Rossby wave train into the mid-latitude troposphere, which, in turn, influences the upward propagation of planetary waves into the polar vortex.
Model studies suggest that, in general, the HT effect is sensitive to the state of the polar vortex (Anstey and Shepherd, 2014), though in some models QBO teleconnections are also effected by circulation biases (Karpechko et al., 2021). A dependency on the vortex strength is one possible reason for the observed intra-seasonal variations and inter-hemisphere differences in extratropical QBO response: in the NH the HT effect is most robust in December and January (Zhang et al., 2019), while in the SH the winter polar vortex is much stronger (Sect. 2.1) and the response is more distinctive around the time of the final warming (Baldwin and Dunkerton, 1998). Interactions found between the QBO stratospheric teleconnections and the solar cycle (Naito and Hirota, 1997) and El Niño–Southern Oscillation (ENSO; Garfinkel and Hartmann, 2007) make the causes of these differences uncertain as both the QBO and polar vortex variability are, separately, impacted by these longer timescale modes of variability. The QBO altitudes which exert the strongest influence on the extratropics is another uncertain aspect (Anstey et al., 2022b).
4.2 Interruptions to the QBO
In February 2016 a shallow layer of westward winds began to form at the Equator within the decaying eastward phase of the QBO (Newman et al., 2016; Osprey et al., 2016). At the time this was a complete surprise, and over the next few months the usual oscillation in the equatorial winds appeared to cease (Fig. 11), raising concerns among leading researchers of the QBO entering a “death spiral” (Dunkerton, 2016) and disappearing altogether. We now know that this did not happen, and by late 2016 the regular cycling of the equatorial winds had recommenced (Fig. 11), albeit with the phase progression shifted from what would be expected if the interruption had not occurred (Anstey et al., 2021).
Compared to previously observed QBO cycles, the anomalous behaviour in 2016 was unprecedented (Newman et al., 2016; Osprey et al., 2016). It could not be accounted for by the established canonical model of the QBO, which relies only on the vertical transport of momentum (Sect. 3.1). Instead, Osprey et al. (2016) and Coy et al. (2017) attributed the anomalous westward acceleration near 40 hPa to enhanced horizontal EP flux, F(ϕ) (Eq. 3), entering the tropics from the NH. Arguably this was the first observational evidence of the extratropical stratosphere directly influencing the variability of the tropical stratosphere, as opposed to indirectly though the meridional circulation. Further evidence for the direct influence was obtained when the QBO was surprisingly interrupted again in December 2019, though this time the horizontally propagating Rossby waves came from the SH (Anstey et al., 2021).
A dynamical explanation for the interruptions is still in its infancy. While several studies have examined the role of different wave types and found that tropical mixed Rossby-gravity waves have an important role in the anomalous westward accelerations (Lin et al., 2019; Kang et al., 2020; Kang and Chun, 2021), others (Hitchcock et al., 2018) have stressed the importance of feedback mechanisms. Nonetheless, all conclude that during the disrupted cycles there was a significant extratropical influence on the variability in the tropical stratosphere. One consequence of this direct influence by the extratropical waves is that the paradigm in which the tropical zonal winds retain memory from year to year (the low-latitude “fly-wheel” effect; Scott and Haynes, 1998), and thereby provide a mechanism for inter-annual variability, is possibly less appropriate than previously thought and may need to be reconsidered once a full understanding of the QBO interruptions is obtained.
5.1 Stratosphere resolving models
First attempts to investigate stratospheric dynamics in a general circulation model (GCM) were by Manabe and Hunt (1968), though the model they used was only hemispheric with a simulation of less than 1 year. In general, early GCMs typically neglected the stratosphere based simply on its small fraction (∼17 %) of the atmospheric mass and need to optimize use of available computing resources. When the stratosphere did feature in GCMs (e.g. Kasahara and Sasamori, 1974; Fels et al., 1980), long simulations of the variability were not feasible due, again, to computational constraints. Computers used for modelling the atmosphere evolved into supercomputers around 19806, and a number of models subsequently preformed multi-year simulations of the stratosphere (Rind et al., 1988; Boville, 1995; Hamilton, 1995; Manzini and Bengtsson, 1996; Butchart and Austin, 1998). In these simulation the stratosphere was typically closer to radiative equilibrium than observed (cf. Sect. 2.1) with significant cold biases in the high latitudes, especially during the SH winter and spring (the so-called “cold-pole problem”), and the QBO was virtually absent from the tropical stratosphere (Pawson et al., 2000).
Biases in the simulated stratospheres are critical as, starting with Boville (1984), it has become clear that the simulated tropospheric circulation is more sensitive to the stratosphere than would be expected from the stratosphere's relatively small mass (see also Sect. 6.3). Likewise, when Farman et al. (1985) discovered a hole in the ozone layer over Antarctica, the first versions of the models developed to include chemistry (chemistry-climate models or CCMs) for assessing ozone changes were limited by the stratospheric temperature biases (Austin et al., 2003). Improvements in the simulated stratosphere were also found desirable for numerical weather-prediction models in order to better assimilate satellite radiance measurements that are often significantly weighted in the stratosphere (English et al., 2000; Polavarapu et al., 2005).
The cold pole problem resulted from a diabatic circulation (Sect. 2.1) that was too weak due to deficiencies in the wave drag ascribed to the absence of gravity waves (McLandress, 1998). Increasing resolution was found to partially alleviate the problem (Hamilton et al., 1999), though more significant was the implementation of parametrizations of non-orographic gravity waves (NOGWs) to supply the missing forcing from sub-grid-scale waves (Manzini et al., 1997; Scaife et al., 2002). Despite their simplicity, and not being well constrained by observations (Plougonven et al., 2020), such schemes enabled models to simulate well the polar night jet in both hemispheres, though there is still work to be done on improving the variability of the jets (Butchart et al., 2011; Ayarzagüena et al., 2020; Hall et al., 2021b). For example, while the latest state-of-the-art climate models simulate the frequency of occurrences of SSWs reasonably well (Baldwin et al., 2021), the models are persistently biased towards an under-representation of split compared to displaced vortex events (Hall et al., 2021b).
When Scaife et al. (2000) first tested NOGW parametrizations in their GCM, they discovered that a QBO-like oscillation of descending eastward and westward winds appeared in the tropical stratosphere. Prior to this the QBO was generally absent from GCMs or very weak (Cariolle et al., 1993). An oscillation of realistic amplitude had been obtained by Takahashi (1996) without parametrized NOGW drag but only by using fine vertical resolution (∼500 m) and substantially reduced sub-grid-scale diffusion. Spontaneous QBO-like phenomena were also obtained in other simplified GCMs without a NOGW parametrization by increasing vertical resolution (Horinouchi and Yoden, 1998; Hamilton et al., 1999). Nonetheless, today, climate and seasonal prediction models that are able to simulate a QBO nearly always do so by implementing parametrizations of NOGWs (Butchart et al., 2018; Bushell et al., 2022; Richter et al., 2022; Stockdale et al., 2022). The number of such models has grown substantially since the pioneering work of Scaife et al. (2002), but, so far, the quality of the simulated QBOs has, on average, not improved much (Richter et al., 2020).
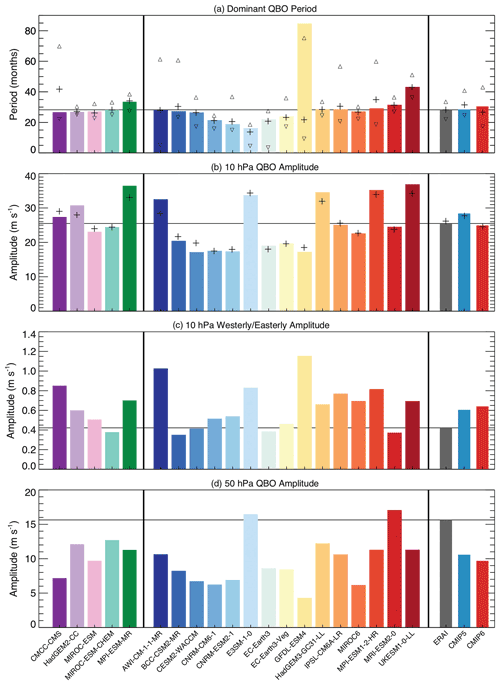
Figure 14(a) QBO periods, (b) 10 hPa QBO amplitude, (c) 10 hPa ratio of westerly (eastward) to easterly (westward) QBO amplitude, and (d) 50 hPa QBO amplitude for models that participated in phases 5 (leftmost five bars) and 6 (middle 15 bars) of the Coupled Model Intercomparison Project (CMIP; Eyring et al., 2016; Taylor et al., 2012). CMIP5 and CMIP6 ensemble means are compared on the right with the corresponding ERA-Interim (Dee et al., 2011) results. The triangles in panel (a) indicate the range of periods. Periods and amplitude obtained using different diagnostics are shown by the + symbol in panels (a) and (b) to confirm robustness of the conclusions. Figure 2 from Richter et al. (2020). © American Geophysical Union.
One characteristic of the QBO that is generally well simulated is the mean period (Fig. 14a), which is typically accomplished by tuning the (weakly constrained) parametrized NOGW drag (Bushell et al., 2022; Garfinkel et al., 2022). More difficult to achieve is the correct vertical structure with models persistently under-representing the strength of the oscillation in the lower stratosphere (Richter et al., 2020; Bushell et al., 2022), despite being able to simulate, on average, realistic amplitudes in the middle stratosphere (cf. Fig. 14b and d). There are also problems in reproducing the correct phase asymmetry (Schenzinger et al., 2017). On average the eastward phase is relatively too strong in models (Fig. 14c), while in initialized simulations the models struggle to maintain the strength of the westward phase (Stockdale et al., 2022). In general the models under-represent cycle-to-cycle variability (Bushell et al., 2022).
Problems in simulating the QBO are largely attributed to uncertainties in parametrizing NOGWs (Bushell et al., 2022). Improving the parametrizations is an area of active research and recent developments have included more physically based representations of the source of NOGWs (Richter et al., 2010; Lott and Guez, 2013; Bushell et al., 2015). Resolved equatorial waves also contribute to the QBO forcing, particularly Kelvin waves during the eastward phase (Pahlavan et al., 2021b). Again there is uncertainty (spread) among models in the resolved waves (Kelvin and mixed Rossby-gravity waves) linked to the convective sources as well as resolution and mean wind biases, with a particular affinity between the resolved wave forcing and model vertical resolution (Holt et al., 2022). Reducing the uncertainty in the wave forcing (parametrized and resolved) is expected to lead to improvements in the simulations of the QBO (Anstey et al., 2022b). In turn, this will impact on the representation of QBO extratropical teleconnections (Sect. 4.1) in the models which are known to be sensitive to biases in the QBO (Anstey et al., 2022c) as well as the mean stratospheric circulation (Karpechko et al., 2021).
5.2 Predictability of the stratosphere
Predicting stratospheric variations can be done either empirically using statistical methods or, as considered here, dynamically using numerical models. Miyakoda et al. (1970) pioneered attempts to develop numerical predictions of the stratosphere, but their 14 d GCM simulation for March 1965 was not successful at capturing the sudden warming that occurred. The February 1979 SSW was the first to be successfully simulated and also the first observed from space (Palmer, 1981a, b) using newly introduced operational temperature soundings of the stratosphere (Miller et al., 1980). The successful simulation of the 1979 SSW by Butchart et al. (1982) was initialized 5 d prior to the peak of the warming but relied on prescribed lower boundary conditions at the tropopause. In subsequent numerical forecasts Simmons and Strüfing (1983) and Mechoso et al. (1985) found this SSW was predictable up to 10 and 5 d ahead, respectively.
With more SSWs and concomitant case studies (Mukougawa and Hirooka, 2004; Allen et al., 2006; Tripathi et al., 2016; Rao et al., 2018) the current consensus is that SSWs can, in general, be deterministically predicted 1 to 2 weeks in advance (Domeisen et al., 2020b), with higher skill more likely from models with enhanced representation of the stratosphere (Allen et al., 2006; Marshall and Scaife, 2010; Song et al., 2020). For a single model predictive skill varies between SSWs (Taguchi, 2016; Karpechko, 2018; Rao et al., 2019) due to differences in the phenomenology and generation mechanisms for vortex-splitting and vortex-displacing events (Sect. 2.5). These differences contribute to determining if the predictability arises mostly from the stratosphere or from the troposphere (Sun et al., 2012). Predictability arising from the troposphere is sensitive to model biases affecting planetary waves and depends on their propagation timescales (Noguchi et al., 2016), whereas predictability arising from the stratosphere is more likely to depend on the background stratospheric state prior to an SSW (de la Cámara et al., 2017). In general, vortex splitting appears more difficult to forecast than a vortex displacement (Taguchi, 2018a; Song et al., 2020).
Compared to the troposphere the extratropical stratosphere exhibits extended predictability (Waugh et al., 1998; Lahoz, 1999), though for extreme vortex events such as an SSW or, alternatively a polar vortex intensification, the predictability is still limited by initial condition uncertainty and model errors (Tripathi et al., 2015). Among forecast systems there is, nonetheless, an affinity between higher skill in the stratosphere and higher skill in the troposphere (Domeisen et al., 2020b), and most systems consistently predict polar vortex intensification and final warmings better than SSWs (Ichimaru et al., 2016; Domeisen et al., 2020b). For the NH winter/spring stratosphere deterministic forecast skill is generally limited to a range of 1 to 2 weeks (Domeisen et al., 2020b). In the SH perturbations to the polar vortex in winter persist into spring due to the reduced intraseasonal variability (Fig. 8) resulting from the weaker planetary wave forcing (Byrne and Shepherd, 2018). Hence, the SH stratosphere is potentially predictable on longer timescales, as is evident in the significant skill found by Seviour et al. (2014) in the prediction of the strength of the Antarctic stratospheric polar vortex in spring at 1-month-average lead times (Fig. 15).
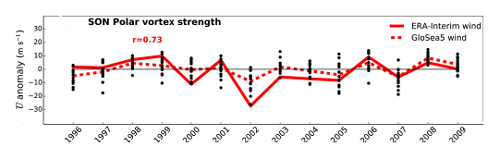
Figure 15September-to-November mean anomalies in the zonal mean zonal wind at 10 hPa and 60∘ S in ERA-Interim (solid curve) and hindcasts (black dots) initialized near 1 August. The dashed curve is the ensemble mean with the interannual correlation with the reanalysis of 0.73. Figure 2a from Seviour et al. (2014), © Seviour et al. (2014), https://creativecommons.org/licenses/by/4.0/ (last access: 1 November 2022).
During the boreal winter the extratropical stratosphere has also been found to be predictable in a probabilistic sense on seasonal timescales well beyond the deterministic range of forecast skill (Scaife et al., 2016; Taguchi, 2018b; Portal et al., 2022). Scaife et al. (2016) noted that in seasonal forecasts capable of reproducing the overall climatological frequencies of SSWs and strong polar vortex (SPV) events well, the proportion of ensemble members predicting the occurrence of an SSW or SPV event varied from year to year (Fig. 16). For winters in which an SSW (SPV) was “observed” (based on proxy observations derived from the forecast ensemble – see Scaife et al., 2016, for details), the proportion of ensemble members forecasting a SSW (SPV) increased, on average, by 12 %, indicating potential probabilistic forecast skill on a seasonal timescale with significance beyond the 95 % level (Scaife et al., 2016). Most likely contributors to this probabilistic skill are the ENSO and the QBO, though, on average, the latest state-of-the-art seasonal forecast systems overestimate the anomalous wave forcing of the polar vortex due to ENSO while underestimating the modulation of the strength of the vortex by the QBO, at least for a hindcast period when the observed interannual variability of the polar vortex was significantly affected by the QBO (Portal et al., 2022).
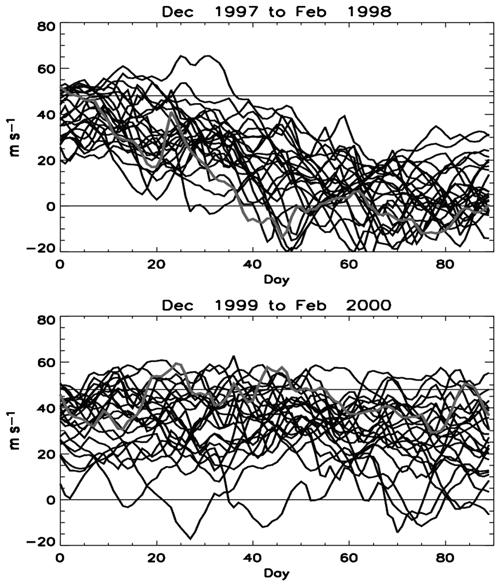
Figure 16Ensemble forecast evolution of zonal wind in the stratosphere. Zonal mean winds are shown (10 hPa, 60∘ N) in two different winters, with 24 ensemble members per winter. The horizontal lines show the threshold for SSW (0 m s−1) events and SPV (48 m s−1) events. The two winters shown exhibit quite different predicted probability of a SSW or SPV event, indicating the potential for forecasting the risk of these events well beyond the deterministic range of a few weeks. Adapted from Fig. 1 of Scaife et al. (2016). © Crown Copyright Met Office, https://creativecommons.org/licenses/by/4.0/ (last access: 1 November 2022).
Prediction skill of the QBO itself is very high in the lower to middle stratosphere on sub-seasonal to seasonal timescales (Lim et al., 2019b; Coy et al., 2022). Out to 1 year, high skill is still obtained for predictions of the phase progression (Coy et al., 2020), though initialized forecasts are generally less successful at maintaining adequate QBO amplitudes (Stockdale et al., 2022). This is largely attributed to weaknesses in all models in predicting the development of a sufficiently strong westward phase which, in turn, can be linked to inadequacies in overall representation of the QBO in the models (Coy et al., 2022; Stockdale et al., 2022). Beyond 12 months, decadal forecast systems have been found to exhibit predictive skill up to 4 years for the QBO phase (Pohlmann et al., 2013; Scaife et al., 2014), with potential for extending this further by improving the representation and prediction of ozone variability in the models (Pohlmann et al., 2019). Enhanced ENSO prediction skill also has potential for extending lead times for skillful QBO predictions as strong ENSO events have been found to lock the QBO phase across ensemble members in uninitialized simulations (Christiansen et al., 2016; Serva et al., 2020).
Exploiting the skillful multi-year QBO predictions is currently frustrated by deficiencies in the amplitudes and vertical structure of the predicted QBOs (Pohlmann et al., 2019). Multi-model results show that similar deficiencies are already present on the seasonal-to-annual timescale and almost certainly contribute to a lack of skill in predicting the QBO's extratropical winter teleconnections beyond the first month (Stockdale et al., 2022). The two recent interruptions to the QBO (Sect. 4.2) add further uncertainty to the robustness of the QBO as a source of predictability as the predictable signal was lost during each interruption before re-emerging a few months later but with a significant shift in phase from what would have been expected (Anstey et al., 2021). Neither interruption was predicted by operational seasonal forecasts (Osprey et al., 2016; Anstey et al., 2021), though for the 2016 event Watanabe et al. (2018) found skill at lead times of around 1 month. Predictability on this timescale is consistent with the events initiated from the extratropics (Sect. 4.2) but much reduced from the timescales associated with the QBO's uninterrupted quasi-regular cycling.
6.1 Middle and high latitudes
When Scherhag (1952) first discovered SSWs he also presented tentative evidence that their effects reach the surface. Similarly, over a decade after co-discovering the QBO Ebdon (1975) found evidence suggesting that it features in determining the character of the NH tropospheric circulation. The earliest model results linking tropospheric circulation changes to variations in the stratospheric polar vortex are those published by Boville (1984), with concurrent theoretical advances (Hoskins et al., 1985; Haynes and Shepherd, 1989; Haynes et al., 1991) further supporting the possibility of a downward influence. Nonetheless, up until the end of the twentieth century, the prevalent view was that the dynamical coupling between the troposphere and stratosphere was mostly one-way with the stratosphere responding to forcing from below.
The paradigm shift to a two-way coupling arose from analysis of the Northern Annular Mode and Southern Annular Mode (NAM and SAM, respectively; Thompson and Wallace, 2000). These are the leading patterns of the large-scale variability of the extratropical circulation and dominate variability on intraseasonal to interdecadal timescales. A manifestation of the annular modes in the troposphere is a fluctuation in the latitudinal position of the jet stream, while in the stratosphere the characteristic feature is a fluctuation in the strength of the polar vortex (Kidston et al., 2015). Annular modes in the stratosphere and troposphere appear to be coupled with occurrences of a weaker polar vortex correlated with equatorward shifts of the jet stream and vice versa for occurrences of a stronger polar vortex (Kidston et al., 2015). The discovery that NAM anomalies progress downward from the stratosphere all the way to the Earth's surface is most often credited to Baldwin and Dunkerton (1999), though other studies had previously noted stratospheric circulation anomalies extending down into the upper troposphere (Boville, 1984; Kodera et al., 1990; Perlwitz and Graf, 1995; Kuroda and Kodera, 1998; Thompson and Wallace, 1998). Downward progression of SAM anomalies from the stratosphere to the surface was first reported by Thompson and Solomon (2002) in association with SH climate change.
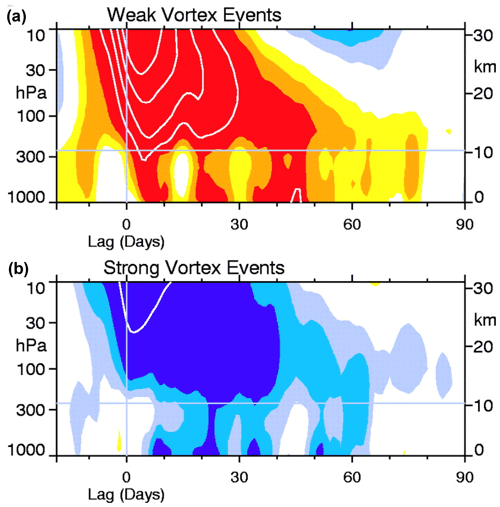
Figure 17Dripping paint diagram. Composites of a non-dimensional NAM index (Baldwin and Dunkerton, 2001) showing descent of NAM anomalies from the stratosphere into the troposphere for (a) 18 weak vortex events (e.g. SSWs) and (b) 30 strong vortex events. The approximate location of the extratropical tropopause is indicated by the horizontal line. In panel (a) the weak events corresponding to negative values of the index (yellow and red shading) are determined by the dates on which the 10 hPa annular mode values cross −3.0. In panel (b) the strong events corresponding to positive values of the index (blue shading) are determined by the dates on which the 10 hPa index crosses +1.5. The shading is at intervals of 0.25 and the white contours at intervals of 0.5. Adapted from Fig. 2 of Baldwin and Dunkerton (2001). © American Association for the Advancement of Science.
Persistence times for annular mode anomalies are longest in the stratosphere, but in months when the polar vortex is most active (January–February in the NH and November–December in the SH – see Sect. 2.4) and strongly coupled to the troposphere, timescales in the troposphere lengthen (Kidston et al., 2015; Gerber and Martineau, 2018). In these months anomalous values of the annular modes in the stratosphere are often followed by anomalies of the same sign in the troposphere, which sometimes persist for up to 2 months in the NH (e.g. Fig. 17) and even longer in the SH (Thompson et al., 2005). A slight delay before the occurrence of the concomitant tropospheric anomalies (Fig. 17) suggests the possibility that the anomalies are propagating downward (Baldwin and Dunkerton, 2001), and, indeed, model studies have demonstrated that there is a genuine physical downward influence with the stratosphere affecting behaviour in the troposphere and at the surface as reviewed by Kidston et al. (2015).
On the other hand, annular modes derived from EOFs (Thompson and Wallace, 2000; Baldwin and Dunkerton, 2001; Thompson et al., 2005) are not necessarily physical modes of variability (Sheshadri et al., 2018), and formulating a dynamical theory for the downward propagation of anomalies is still a work in progress. Given the comparatively light weight of the stratosphere, its downward influence almost certainly results from a sensitivity of tropospheric dynamics to changes in the stratosphere with eddy feedbacks (Song and Robinson, 2004; Smy and Scott, 2009; Hitchcock and Simpson, 2014, 2016; Runde et al., 2016; Rupp and Birner, 2021) fundamental for enhancing the tropospheric response and contributing to its persistence. An alternative perspective for the stratosphere's downward effect on the Atlantic jet is the strong response results from a regime shift between three preferred jet positions rather than a simple latitudinal movement in jet position (Maycock et al., 2020; Goss et al., 2021). Proposed mechanisms for communicating the dynamical effects from the stratosphere to the troposphere include non-local PV inversion (Charlton et al., 2005), the downward effect of an induced secondary meridional circulation (Song and Robinson, 2004), and the effects resulting from upward-propagating waves either being reflected back downward or changing the refractive properties of the lower stratosphere through wave–mean-flow interactions (Perlwitz and Harnik, 2004). However, none of these proposed dynamical mechanism can account for all aspects of the stratosphere's downward influence.
One complicating factor is that the anomalous stratospheric events are quite diverse and do not always extend downward into the troposphere or, indeed, to the surface (Karpechko et al., 2017). In the NH the diversity is largely associated with the different types of SSWs (Sect. 2.5), with a surface impact only observed for about two-thirds of the events (Domeisen, 2019; Hall et al., 2021a). Characteristics which determine whether an SSW has a downward influence remain elusive, and it is still not possible to foresee at the onset of an SSW if it is likely to be followed by a discernible surface impact (Baldwin et al., 2021). When there is a downward influence the surface impacts of split events are seen, on average, about 1 week sooner than the impacts of displacement events, at least for reanalysis data (Seviour et al., 2016; Hall et al., 2021a). On the other hand, model results from Maycock and Hitchcock (2015) indicate no significant dependency on SSW type and show that there is probably insufficient evidence to establish a difference between impacts by split and displacement events.
Following from studies of descending annular mode anomalies, it is now apparent that there is an affinity between occurrences of extreme surface weather and the strength of the polar vortex (Kidston et al., 2015; Domeisen and Butler, 2020), and also the phase of the QBO due to its teleconnections to the polar vortex (Sect. 4.1). Extreme weather events involving a significant contribution from the stratosphere have been catalogued by Domeisen and Butler (2020), and they found them to be wide ranging with the stratospheric connection more firmly established for some than others. The connection in the NH is most prominent and robust in the Atlantic basin (Charlton-Perez et al., 2018), with a weakening of the polar vortex, or SSW, often associated with cold weather over Europe and the eastern USA (King et al., 2019) and cold air outbreaks over the northeastern Atlantic (Afargan-Gerstman et al., 2020). In contrast, an unusually strong Arctic polar vortex, as often occurs during the QBO eastward phase (Sect. 4.1), is associated with stronger surface winds and more intense cyclones with increased the risk of storms and extreme rainfall over northwest Europe (Kidston et al., 2015).
A weakening of the SH polar vortex and negative SAM index in the lower stratosphere generally leads to hot dry extremes over Australia (Lim et al., 2019a, 2021), cooler wetter conditions over southern South America (Lim et al., 2018) and higher Antarctic surface temperatures, except for the Palmer Peninsula, which is more likely to experience cold dry conditions (Thompson et al., 2005; Lim et al., 2018). A positive SAM index often brings significant cooling to Antarctica and much of Australia, warming to the Palmer Peninsula, and warm dry conditions to southern South America, New Zealand and Tasmania, while Australia and South Africa are more likely to experience anomalously wet conditions (Gillett et al., 2006; Garreaud, 2018).
6.2 Low latitudes
The influence of the stratosphere on the tropical troposphere was independently reviewed recently by Haynes et al. (2021), and, hence, only a selection of the more significant dynamical developments are covered here. First indications of a possible coupling between the stratosphere and tropical troposphere came when Gray (1984) noted a correlation between the frequency of Atlantic hurricanes and the phase of the QBO, though somewhat earlier Angell et al. (1969) had tentatively suggested that the QBO had a role in determining the frequency of Pacific typhoons. Later studies (Ho et al., 2009; Camargo and Sobel, 2010), however, questioned the robustness of such relationships, and a convincing dynamical explanation is still wanting (Haynes et al., 2021; Hitchman et al., 2021).
Tropical dynamics differ from extratropical dynamics due to the smallness of the Coriolis parameter, which implies that, unlike in the extratropics (Sect. 6.1), the vertical scales inferred from balance dynamics are generally too shallow to potentially explain a coupling between the stratosphere and troposphere. Instead, proposed mechanisms for a tropical pathway between the stratosphere and troposphere are commonly based on the paradigm that variability at the tropopause and in the lower stratosphere modulates behaviour throughout the depth of the tropical troposphere (Haynes et al., 2021). While the variability in the tropical stratosphere is dominated by the QBO (Sect. 3), 3 km, or so, above the tropopause the descending alternating eastward and westward wind regimes begin to weaken significantly (Fig. 11) and do not penetrate into the troposphere. Driven by the induced secondary circulation, the concomitant temperature QBO (Sect. 3.1) extends slightly lower with an identifiable signal observed up to ∼15∘ on either side the Equator near the tropopause, albeit small (∼0.5 K) compared to the dominant annual cycle (Sect. 3). The resultant temperature and circulation anomalies at the tropopause and in the lower stratosphere exert a downward influence on tropical convection, which in turn plays a major role in coupling the QBO to the tropical troposphere (Haynes et al., 2021). Spatial variations in convection partially explain why the QBO signal in the troposphere is no longer predominately zonally symmetric as it was in the stratosphere but, so far, none of the physical mechanisms proposed can account for all aspects of the large geographical variations in the QBO's downward influence on the tropical troposphere (Haynes et al., 2021).
The QBO's influence on tropical convection is the main reason for its involvement (Yoo and Son, 2016; Nishimoto and Yoden, 2017; Klotzbach et al., 2019; Martin et al., 2021) with the Madden–Julian oscillation (MJO), which dominates intraseasonal variability in the tropical troposphere (Zhang, 2005). During the NH winter up to 40 % of the inter-annual variations in the MJO amplitude are explained by a coupling to the QBO (Son et al., 2017), with the MJO stronger and more persistent, by up to 10 d, when the QBO is westward in the lower stratosphere (Yoo and Son, 2016; Martin et al., 2021). In contrast, an eastward QBO phase in the lower stratosphere favours a weaker-than-normal MJO during NH winter (Yoo and Son, 2016).
Knowledge of the QBO–MJO relationship is only just emerging (Klotzbach et al., 2019), and there is still plenty to do in developing a working mechanism (Haynes et al., 2021; Martin et al., 2021). The relationship is, nonetheless, particularly relevant as it implies a potential pathway coupling the stratosphere to the extratropical troposphere (cf. Sect. 6.1) via the MJO's teleconnections to high latitudes (Anstey et al., 2022b). The corresponding ramifications for the extratropics of this modulation of the MJO's global teleconnections by the QBO are reviewed in Martin et al. (2021), and, therefore, this aspect of the QBO–MJO relationship is not considered here.
The tropical troposphere and MJO are also affected by SSWs (Kodera and Yamada, 2004; Kodera, 2006; Bal et al., 2017; Noguchi et al., 2020; Wang et al., 2020a; Yoshida and Mizuta, 2021). One proposed mechanism is that the increased wave driving during an SSW strengthens the mean meridional (Brewer–Dobson) circulation and cools the tropical lower stratosphere and tropopause. The anomalies created then impact tropical convection (Kodera et al., 2011) in a similar way to the anomalies resulting from the QBO's secondary circulation. Tropopause level PV intrusions from the subtropics during an SSW also affect the upper tropical troposphere (Albers et al., 2016) and represent an alternative subtropical pathway from the stratosphere to tropical troposphere (Haynes et al., 2021).
Ramifications of the stratosphere's influence on the tropical troposphere include an enhancement of convective activity and precipitation over the tropical west Pacific and a suppression over the equatorial central and east Pacific when the QBO is westward in the lower stratosphere, at least for the annual mean (Haynes et al., 2021). During SSWs equatorial convection is enhanced south of the Equator and suppressed to the north, especially for split vortex events (Bal et al., 2017), while tropical cyclones are generally more intense (Yoshida and Mizuta, 2021). Monsoon intensity and rainfall appear to be sensitive to the QBO phase with, for example, the East Asian winter monsoon weaker, on average, when the QBO is westward compared to when it is eastward at 70 hPa (Ma et al., 2021). Also, over East Asia MJO-related precipitation anomalies are between 40 % and 70 % larger during the QBO westward phase than during the eastward phase, depending on the phase of the MJO (Kim et al., 2020).
6.3 Enhancing tropospheric predictions
The stratosphere's powerful downward influences and longer prediction timescales (Sect. 5.2) are reasons why the stratosphere matters for tropospheric predictions (Scaife et al., 2022). Models with better-resolved stratospheres generally produce superior simulations of the surface climate (Hardiman et al., 2012; Kawatani et al., 2019) and more skillful forecasts on sub-seasonal to seasonal timescales (e.g. Fig. 18; Roff et al., 2011; Charron et al., 2012; Butler et al., 2016; Marshall et al., 2017; Domeisen et al., 2020a), with more accurate stratospheric initial conditions (Jia et al., 2017) and variability (Tripathi et al., 2015) further enhancing forecast skill. In the extratropics, predictive skill is enhanced (Sigmond et al., 2013) following SSWs, and, in April, skill can be gained from a knowledge of the vertical structure of the final warming (Hardiman et al., 2011; Butler et al., 2019). In the tropics, MJO predictability is influenced by the QBO (Marshall et al., 2017; Lim et al., 2019b; Wang et al., 2019).
Figure 18Average improvement in predictive skill for geopotential height anomalies in the SH poleward of 60∘ S in ensembles of 30 d forecasts from mid-November for the years 1979–2008 when the vertical resolution in the forecast model is increased above 100 hPa (Roff et al., 2011). In the troposphere, improvements of ∼5 % are seen 3–4 weeks into the forecasts. Note the non-linear scale for the shading. Figure 2a from Roff et al. (2011). © American Geophysical Union.
Another reason why the stratosphere matters for extratropical predictions is the pathways it provides to potential sources of extended range skill lying outside the stratosphere such as ENSO (Cagnazzo and Manzini, 2009; Ineson and Scaife, 2009; Butler et al., 2014), Eurasian snow cover (Hardiman et al., 2008; Garfinkel et al., 2020a) and Arctic sea ice (Kim et al., 2014; Zhang et al., 2018; Kretschmer et al., 2020). Multi-year skill arising from the solar cycle (Gray et al., 2013; Dunstone et al., 2016) and volcanic eruptions (Bittner et al., 2016) also involves the stratosphere, though the possible mechanisms are not considered here. A concurrent independent perspective of these aspects of the stratosphere's role in long-range prediction can, instead, be found in Scaife et al. (2022).
Although the observed dynamical variability of the stratosphere is reasonably well understood in terms wave–mean-flow theory, the observations themselves continue to surprise researchers just as the original discoveries of SSWs and the QBO had surprised meteorologists of the time. In 2002, a SSW was recorded for the first time in the SH (Baldwin et al., 2021), and in 2016, and again in 2019, the QBO's near-repeatable cycles of eastward and westward winds that had been observed continuously since its discovery were interrupted (Newman et al., 2016; Osprey et al., 2016; Anstey et al., 2021). These interruptions prompted a reassessment of the extent to which the extratropical stratosphere could influence the tropics (Sect. 4.2), though the efficacy of the underlying canonical model remained strong. On the other hand, the interruptions, as well as the occurrence of the SH SSW, suggest the observational record may not be long enough (e.g. just 27 QBO cycles prior to 2016) to properly quantify the full range of dynamical variability in the stratosphere. Consequently, it is not possible to determine, with confidence, if such rare or extreme events are part of the natural dynamical variability or a sign of human activity affecting the stratosphere (Wang et al., 2020b; Anstey et al., 2021; Jucker et al., 2021).
Internal multi-year variability of the polar vortex seen in climate models (Butchart et al., 2000) is another outstanding issue that can only be fully addressed with more years of observations. Simple models have demonstrated that there are potential internal dynamical mechanisms that can drive low-frequency variability of the polar vortex, even in the absence of other external forcings (Hatfield and Scott, 2019). In addition, circumstantial evidence for low-frequency variability is seen in the decadal variations in the frequency of occurrences of SSWs deduced from surface observations (Domeisen, 2019). Whether or not this circumstantial evidence is an indication of internal stratospheric variability (Butchart et al., 2000) or is due to variations in stratosphere–troposphere coupling on inter-decadal timescales (Manzini et al., 2012; Woo et al., 2015; Omrani et al., 2016) remains an open question.
As yet, our understanding of stratospheric variability and its downward influence is not deep enough to know with confidence which aspects and events will have a strong impact at the surface (Baldwin et al., 2021; Haynes et al., 2021). Likewise, the coupling between the tropical and extratropical stratosphere is not fully understood (Anstey and Shepherd, 2014). Current models struggle in representing these teleconnections (Elsbury et al., 2021; Anstey et al., 2022c) and also teleconnections to the troposphere. A more in-depth understanding of the mechanisms will therefore be useful for identifying which aspects of the models require further development to enable them to more accurately predict those surface events and extremes that have an affinity with the stratospheric variability.
Another outstanding issue is how the stratospheric variability will respond to climate change and what feedbacks there will be on the tropospheric climate. In the extratropics there is currently large uncertainty over the projected response due to the near balance between opposing effects of increased CO2 radiative cooling and increased adiabatic heating from a faster Brewer–Dobson circulation (Ayarzagüena et al., 2020). On the other hand, in the tropics a projected weakening of the QBO appears robust (Kawatani and Hamilton, 2013; Butchart et al., 2020; Richter et al., 2022), though, again, there is large uncertainty over the response of the QBO period (Richter et al., 2022). The uncertainties in the QBO response are attributed to inadequacies in the representation (parametrization) of small-scale gravity waves within models due to the lack of observational constraints (Richter et al., 2022). It has also been suggested that the rudimentary representation of small-scale gravity waves in models contributes to the uncertainties in the extratropical response (Kidston et al., 2015). Reducing these uncertainties is important since through the stratosphere's downward influence they can contribute significantly to uncertainties in projections for regional climate (Kidston et al., 2015; Simpson et al., 2018) and extremes (Domeisen and Butler, 2020).
Finally, for over 50 years it has been recognized that the stratosphere is extremely vulnerable to the effects of human activity (Tuck, 2021), with the well being of the ozone layer of particular concern. The Montreal Protocol was agreed to safeguard the ozone layer, but a range of human activities, such as those causing wild fires (Stocker et al., 2021), speculative geoengineering proposals for mitigating climate change (Tilmes et al., 2018; Smith et al., 2022), space tourism and high-altitude leisure flights by dangerously polluting rocket-powered hobby aeroplanes (Larson et al., 2017; Ryan et al., 2022), are all likely to affect the variability in the stratosphere and hence surface weather and climate. Potentially, this could increase the risk of disastrous extremes, and hence there is the need for continued research and monitoring of the stratosphere and new international agreements to regulate human activities that affect stratospheric variability but have little or no societal benefits.
ECMWF ERA5 data are accessible via the climate data store (https://doi.org/10.24381/cds.adbb2d47, Hersbach et al., 2018), and ERA-Interim data are available online (https://apps.ecmwf.int/datasets/data/interim-full-daily/levtype=sfc/, European Centre for Medium-Range Weather Forecasts, 2022). MERRA2 data (Gelaro et al., 2017) used in Fig. 8 are freely available from NASA Ozone Watch (https://ozonewatch.gsfc.nasa.gov/, last access: 3 November 2022).
The author has declared that there are no competing interests.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Neal Butchart was supported by the Met Office Hadley Centre Climate Programme funded by BEIS (Department for Business, Energy & Industrial Strategy) and Defra (Department for Environment, Food & Rural Affairs) and by the UK–China Research and Innovation Partnership Fund through the Met Office Climate Science for Service Partnership (CSSP) China initiative as part of the Newton Fund.
This paper was edited by Daniela Domeisen and reviewed by three anonymous referees.
Afargan-Gerstman, H., Polkova, I., Papritz, L., Ruggieri, P., King, M. P., Athanasiadis, P. J., Baehr, J., and Domeisen, D. I. V.: Stratospheric influence on North Atlantic marine cold air outbreaks following sudden stratospheric warming events, Weather Clim. Dynam., 1, 541–553, https://doi.org/10.5194/wcd-1-541-2020, 2020. a
Albers, J. R. and Birner, T.: Vortex preconditioning due to planetary and gravity waves prior to sudden stratospheric warmings, J. Atmos. Sci., 71, 4028–4054, https://doi.org/10.1175/JAS-D-14-0026.1, 2014. a, b
Albers, J. R., Kiladis, G. N., Birner, T., and Dias, J.: Tropical upper-tropospheric potential vorticity intrusions during sudden stratospheric warmings, J. Atmos. Sci., 73, 2361–2384, https://doi.org/10.1175/JAS-D-15-0238.1, 2016. a
Allen, D. R., Coy, L., Eckermann, S. D., McCormack, J. P., Manney, G. L., Hogan, T. F., and Kim, Y.-J.: NOGAPS-ALPHA simulations of the 2002 Southern Hemisphere stratospheric major warming, Mon. Weather Rev., 134, 498–518, https://doi.org/10.1175/MWR3086.1, 2006. a, b
Andrews, D. G.: On the interpretation of the Eliassen-Palm flux divergence, Q. J. Roy. Meteor. Soc., 113, 323–338, https://doi.org/10.1002/qj.49711347518, 1987. a
Andrews, D. G. and McIntyre, M. E.: Planetary waves in horizontal and vertical shear: The generalized Eliassen-Palm relation and the mean zonal acceleration, J. Atmos. Sci., 33, 2031–2048, https://doi.org/10.1175/1520-0469(1976)033<2031:PWIHAV>2.0.CO;2, 1976. a, b, c
Andrews, D. G. and McIntyre, M. E.: Generalized Eliassen-Palm and Charney-Drazin theorems for waves on axismmetric mean flows in compressible atmospheres, J. Atmos. Sci., 35, 175–185, https://doi.org/10.1175/1520-0469(1978)035<0175:GEPACD>2.0.CO;2, 1978. a, b, c, d
Andrews, D. G., Holton, J. R., and Leovy, C. B.: Middle atmosphere dynamics, Academic Press, ISBN: 9780120585762,, 1987. a, b
Angell, J. K. and Korshover, J.: Quasi-biennial variations in temperature, total ozone, and tropopause height, J. Atmos. Sci., 21, 479–492, https://doi.org/10.1175/1520-0469(1964)021<0479:QBVITT>2.0.CO;2, 1964. a, b
Angell, J. K., Korshover, J., and Cotten, G. F.: Quasi-biennial variations in the “centres of action”, Mon. Weather Rev., 97, 867–872, https://doi.org/10.1175/1520-0493(1969)097<0867:QVITOA>2.3.CO;2, 1969. a
Anstey, J. A. and Shepherd, T. G.: High-latitude influence of the quasi-biennial oscillation, Q. J. Roy. Meteor. Soc., 140, 1–21, https://doi.org/10.1002/qj.2132, 2014. a, b, c, d, e
Anstey, J. A., Banyard, T. P., Butchart, N., Coy, L., Newman, P. A., Osprey, S., and Wright, C. J.: Prospect of increased disruption to the QBO in a changing climate, Geophys. Res. Lett., 48, e2021GL093058, https://doi.org/10.1029/2021GL093058, 2021. a, b, c, d, e, f, g, h, i
Anstey, J. A., Butchart, N., Hamilton, K., and Osprey, S. M.: The SPARC Quasi-Biennial Oscillation initiative, Q. J. Roy. Meteor. Soc., 148, 1455–1458, https://doi.org/10.1002/qj.3820, 2022a. a
Anstey, J. A., Osprey, S. M. Alexander, J., Baldwin, M. P., Butchart, N., Gray, L. J., Kawatani, Y., Newman, P. A., and Richter, J. H.: Impacts, processes and projections of the quasi-biennial oscillation, Nat. Rev. Earth Environ., 3, 588–603, https://doi.org/10.1038/s43017-022-00323-7, 2022b. a, b, c, d, e, f, g
Anstey, J. A., Simpson, I. R., Richter, J. H., Naoe, H., Taguchi, M., Serva, F., Gray, L. J., Butchart, N., Hamilton, K., Osprey, S., Bellprat, O., Braesicke, P., Bushell, A. C., Cagnazzo, C., Chen, C.-C., Chun, H.-Y., Garcia, R. R., Holt, L., Kawatani, Y., Kerzenmacher, T., Kim, Y.-H., Lott, F., McLandress, C., Scinocca, J., Stockdale, T. N., Versick, S., Watanabe, S., Yoshida, K., and Yukimoto, S.: Teleconnections of the quasi-biennial oscillation in a multi-model ensemble of QBO-resolving models, Q. J. Roy. Meteor. Soc., 148, 1568–1592, https://doi.org/10.1002/qj.4048, 2022c. a, b
Assmann, R.: Über die Existenz eines wärmeren Luftstromes in der Höhe von 10 bis 15 km (On the existence of a warmer airflow at heights from 10 to 15 km), Sitzber. K. Preuss. Aka., 24, 495–504, 1902. a
Austin, J., Shindell, D., Beagley, S. R., Brühl, C., Dameris, M., Manzini, E., Nagashima, T., Newman, P., Pawson, S., Pitari, G., Rozanov, E., Schnadt, C., and Shepherd, T. G.: Uncertainties and assessments of chemistry-climate models of the stratosphere, Atmos. Chem. Phys., 3, 1–27, https://doi.org/10.5194/acp-3-1-2003, 2003. a, b
Ayarzagüena, B., Charlton-Perez, A. J., Butler, A. H., Hitchcock, P., Simpson, I. R., Polvani, L. M., Butchart, N., Gerber, E. P., Gray, L., Hassler, B., Lin, P., Lott, F., Manzini, E., Mizuta, R., Orbe, C., Osprey, S., Saint-Martin, D., Sigmond, M., Taguchi, M., Volodin, E. M., and Watanabe, S.: Uncertainty in the response of sudden stratospheric warmings and stratosphere-troposphere coupling to quadrupled CO2 concentrations in CMIP6 models, J. Geophys. Res.-Atmos., 125, e2019JD032345, https://doi.org/10.1029/2019JD032345, 2020. a, b
Bal, S., Schimanke, S., Spangehl, T., and Cubasch, U.: Variable influence on the equatorial troposphere associated with SSW using ERA-Interim, J. Earth. Syst. Sci., 126, 1–13, https://doi.org/10.1007/s12040-017-0802-6, 2017. a, b
Baldwin, M. P. and Dunkerton, T. J.: Quasi-biennial modulation of the Southern Hemisphere stratospheric polar vortex, Geophys. Res. Lett., 25, 3343–3346, https://doi.org/10.1029/98GL02445, 1998. a
Baldwin, M. P. and Dunkerton, T. J.: Propagation of the Arctic oscillation from the stratosphere to the troposphere, J. Geophys. Res.-Atmos., 104, 30937–30946, https://doi.org/10.1029/1999JD900445, 1999. a
Baldwin, M. P. and Dunkerton, T. J.: Stratospheric harbingers of anomalous weather regimes, Science, 294, 581–584, https://doi.org/10.1126/science.1063315, 2001. a, b, c, d
Baldwin, M. P. and Holton, J. R.: Climatology of the stratospheric polar vortex and planetary wave breaking, J. Atmos. Sci., 45, 1123–1142, https://doi.org/10.1175/1520-0469(1988)045<1123:COTSPV>2.0.CO;2, 1988. a
Baldwin, M. P., Gray, L. J., Dunkerton, T. J., Hamilton, K., Haynes, P. H., Randel, W. J., Holton, J. R., Alexander, M. J., Hirota, I., Horinouchi, T., Jones, D. B. A., Kinnersley, J. S., Marquardt, C., Sato, K., and Takahashi, M.: The quasi-biennial oscillation, Rev. Geophys., 39, 179–229, https://doi.org/10.1029/1999RG000073, 2001. a, b, c
Baldwin, M. P., Birner, T., Brasseur, G., Burrows, J., Butchart, N., Garcia, R., Geller, M., Gray, L., Hamilton, K., Harnik, N., Hegglin, M. I., Langematz, U., Robock, A., Sato, K., and Scaife, A. A.: 100 years of progress in understanding the stratosphere and mesosphere, Meteor. Mon., 59, 27.1–27.62, https://doi.org/10.1175/AMSMONOGRAPHS-D-19-0003.1, 2019. a
Baldwin, M. P., Ayarzagüena, B., Birner, T., Butchart, N., Butler, A. H., Charlton-Perez, A. J., Domeisen, D. I. V., Garfinkel, C. I., Garny, H., Gerber, E. P., Hegglin, M. I., Langematz, U., and Pedatella, N. M.: Sudden stratospheric warmings, Rev. Geophys., 59, e2020RG000708, https://doi.org/10.1029/2020RG000708, 2021. a, b, c, d, e, f, g, h
Birner, T. and Albers, J. R.: Sudden stratospheric warmings and anomalous upward Wave activity flux, SOLA, 13A, 8–12, https://doi.org/10.2151/sola.13A-002, 2017. a
Bittner, M., Schmidt, H., Timmreck, C., and Sienz, F.: Using a large ensemble of simulations to assess the Northern Hemisphere stratospheric dynamical response to tropical volcanic eruptions and its uncertainty, Geophys. Res. Lett., 43, 9324–9332, https://doi.org/10.1002/2016GL070587, 2016. a
Boljka, L. and Birner, T.: Tropopause-level planetary wave source and its role in two-way troposphere–stratosphere coupling, Weather Clim. Dynam., 1, 555–575, https://doi.org/10.5194/wcd-1-555-2020, 2020. a
Boucher, O.: Stratospheric ozone, ultraviolet radiation and climate change, Weather, 65, 105–110, https://doi.org/10.1002/wea.451, 2010. a
Boville, B. A.: The influence of the polar night jet on the tropospheric circulation in a GCM, J. Atmos. Sci., 41, 1132–1142, https://doi.org/10.1175/1520-0469(1984)041<1132:TIOTPN>2.0.CO;2, 1984. a, b, c
Boville, B. A.: Middle atmosphere version of CCM2 (MACCM2): annual cycle and interannual variability, J. Geophys. Res.-Atmos., 100, 9017–9039, https://doi.org/10.1029/95JD00095, 1995. a
Boyd, J. P.: The noninteraction of waves with the zonally averaged flow on a spherical earth and the interrelationships on eddy fluxes of energy, heat, and momentum, J. Atmos. Sci., 33, 2285–2291, https://doi.org/10.1175/1520-0469(1976)033<2285:TNOWWT>2.0.CO;2, 1976. a
Brewer, A. W.: Evidence for a world circulation provided by measurements of helium and water vapour distribution in the stratosphere, Q. J. Roy. Meteor. Soc., 75, 351–363, https://doi.org/10.1002/qj.49707532603, 1949. a
Bushell, A. C., Butchart, N., Derbyshire, S. H., Jackson, D. R., Shutts, G. J., Vosper, S. B., and Webster, S.: Parameterized gravity wave momentum fluxes from sources related to convection and large-scale precipitation processes in a global atmosphere model, J. Atmos. Sci., 72, 4349–4371, https://doi.org/10.1175/JAS-D-15-0022.1, 2015. a
Bushell, A. C., Anstey, J. A., Butchart, N., Kawatani, Y., Osprey, S. M., Richter, J. H., Serva, F., Braesicke, P., Cagnazzo, C., Chen, C.-C., Chun, H.-Y., Garcia, R. R., Gray, L. J., Hamilton, K., Kerzenmacher, T., Kim, Y.-H., Lott, F., McLandress, C., Naoe, H., Scinocca, J., Smith, A. K., Stockdale, T. N., Versick, S., Watanabe, S., Yoshida, K., and Yukimoto, S.: Evaluation of the quasi-biennial oscillation in global climate models for the SPARC QBO-initiative, Q. J. Roy. Meteor. Soc., 148, 1459–1489, https://doi.org/10.1002/qj.3765, 2022. a, b, c, d, e
Butchart, N.: The Brewer-Dobson circulation, Rev. Geophys., 52, 157–184, https://doi.org/10.1002/2013RG000448, 2014. a, b
Butchart, N. and Austin, J.: Middle atmosphere climatologies from the troposphere-stratosphere configuration of the UKMO's Unified Model, J. Atmos. Sci., 55, 2782–2809, https://doi.org/10.1175/1520-0469(1998)055<2782:MACFTT>2.0.CO;2, 1998. a
Butchart, N. and Remsberg, E. E.: The area of the stratospheric polar vortex as a diagnostic for tracer transport on an isentropic surface, J. Atmos. Sci., 43, 1319–1339, https://doi.org/10.1175/1520-0469(1986)043<1319:TAOTSP>2.0.CO;2, 1986. a, b, c
Butchart, N., Clough, S. A., Palmer, T. N., and Trevelyan, P. J.: Simulations of an observed stratospheric warming with quasi-geostrophic refractive index as a model diagnostic, Q. J. Roy. Meteor. Soc., 108, 475–502, https://doi.org/10.1002/qj.49710845702, 1982. a, b
Butchart, N., Austin, J., Knight, J. R., Scaife, A. A., and Gallani, M. L.: The response of the stratospheric climate to projected changes in the concentrations of well-mixed greenhouse gases from 1992 to 2051, J. Climate, 13, 2142–2159, https://doi.org/10.1175/1520-0442(2000)013<2142:TROTSC>2.0.CO;2, 2000. a, b
Butchart, N., Scaife, A. A., Austin, J., Hare, S. H. E., and Knight, J. R.: Quasi-biennial oscillation in ozone in a coupled chemistry-climate model, J. Geophys. Res.-Atmos., 108, 4486, https://doi.org/10.1029/2002JD003004, 2003. a
Butchart, N., Charlton-Perez, A. J., Cionni, I., Hardiman, S. C., Haynes, P. H., Krüger, K., Kushner, P. J., Newman, P. A., Osprey, S. M., Perlwitz, J., Sigmond, M., Wang, L., Akiyoshi, H., Austin, J., Bekki, S., Baumgaertner, A., Braesicke, P., Brühl, C., Chipperfield, M., Dameris, M., Dhomse, S., Eyring, V., Garcia, R., Garny, H., Jöckel, P., Lamarque, J.-F., Marchand, M., Michou, M., Morgenstern, O., Nakamura, T., Pawson, S., Plummer, D., Pyle, J., Rozanov, E., Scinocca, J., Shepherd, T. G., Shibata, K., Smale, D., Teyssèdre, H., Tian, W., Waugh, D., and Yamashita, Y.: Multimodel climate and variability of the stratosphere, J. Geophys. Res.-Atmos., 116, D05102, https://doi.org/10.1029/2010JD014995, 2011. a, b
Butchart, N., Anstey, J. A., Hamilton, K., Osprey, S., McLandress, C., Bushell, A. C., Kawatani, Y., Kim, Y.-H., Lott, F., Scinocca, J., Stockdale, T. N., Andrews, M., Bellprat, O., Braesicke, P., Cagnazzo, C., Chen, C.-C., Chun, H.-Y., Dobrynin, M., Garcia, R. R., Garcia-Serrano, J., Gray, L. J., Holt, L., Kerzenmacher, T., Naoe, H., Pohlmann, H., Richter, J. H., Scaife, A. A., Schenzinger, V., Serva, F., Versick, S., Watanabe, S., Yoshida, K., and Yukimoto, S.: Overview of experiment design and comparison of models participating in phase 1 of the SPARC Quasi-Biennial Oscillation initiative (QBOi), Geosci. Model Dev., 11, 1009–1032, https://doi.org/10.5194/gmd-11-1009-2018, 2018. a
Butchart, N., Anstey, J. A., Kawatani, Y., Osprey, S. M., Richter, J. H., and Wu, T.: QBO changes in CMIP6 climate projections, Geophys. Res. Lett., 47, e2019GL086903, https://doi.org/10.1029/2019GL086903, 2020. a
Butler, A. H. and Gerber, E. P.: Optimizing the definition of a sudden stratospheric warming, J. Climate, 31, 2337–2344, https://doi.org/10.1175/JCLI-D-17-0648.1, 2018. a
Butler, A. H., Polvani, L. M., and Deser, C.: Separating the stratospheric and tropospheric pathways of El Niño Southern Oscillation teleconnections, Environ. Res. Lett., 9, 024014, https://doi.org/10.1088/1748-9326/9/2/024014, 2014. a
Butler, A. H., Seidel, D. J., Hardiman, S. C., Butchart, N., Birner, T., and Match, A.: Defining sudden stratospheric warmings, B. Am. Meteorol. Soc., 96, 1913–1928, https://doi.org/10.1175/BAMS-D-13-00173.1, 2015. a, b
Butler, A. H., Arribas, A., Athanassiadou, M., Baehr, J., Calvo, N., Charlton-Perez, A., Déqué, M., Domeisen, D. I. V., Fröhlich, K., Hendon, H., Imada, Y., Ishii, M., Iza, M., Karpechko, A. Y., Kumar, A., MacLachlan, C., Merryfield, W. J., Müller, W. A., O'Neill, A., Scaife, A. A., Scinocca, J., Sigmond, M., Stockdale, T. N., and Yasuda, T.: The Climate-system Historical Forecast Project: do stratosphere-resolving models make better seasonal climate predictions in boreal winter?, Q. J. Roy. Meteor. Soc., 142, 1413–1427, https://doi.org/10.1002/qj.2743, 2016. a, b
Butler, A. H., Charlton-Perez, A., Domeisen, D. I., Simpson, I. R., and Sjoberg, J.: Predictability of Northern Hemisphere final stratospheric warmings and their surface impacts, Geophys. Res. Lett., 46, 10578–10588, https://doi.org/10.1029/2019GL083346, 2019. a
Byrne, N. J. and Shepherd, T. G.: Seasonal persistence of circulation anomalies in the Southern Hemisphere stratosphere and its implications for the troposphere, J. Climate, 31, 3467–3483, https://doi.org/10.1175/JCLI-D-17-0557.1, 2018. a
Cagnazzo, C. and Manzini, E.: Impact of the stratosphere on the winter tropospheric teleconnections between ENSO and the North Atlantic and European region, J. Climate, 22, 1223–1238, https://doi.org/10.1175/2008JCLI2549.1, 2009. a
Camargo, S. J. and Sobel, A. H.: Revisiting the influence of the quasi-biennial oscillation on tropical cyclone activity, J. Climate, 23, 5810–5825, https://doi.org/10.1175/2010JCLI3575.1, 2010. a
Cariolle, D., Amodei, M., Déqué, M., Mahfouf, J.-F., Simon, P., and Teyssèdre, H.: A quasi-biennial oscillation signal in general circulation model simulations, Science, 261, 1313–1316, https://doi.org/10.1126/science.261.5126.1313, 1993. a
Charlton, A. J. and Polvani, L. M.: A new look at stratospheric sudden warmings. Part I: climatology and modeling benchmarks, J. Climate, 20, 449–469, https://doi.org/10.1175/JCLI3996.1, 2007. a
Charlton, A. J., O'Neill, A., Berrisford, P., and Lahoz, W. A.: Can the dynamical impact of the stratosphere on the troposphere be described by large-scale adjustment to the stratospheric PV distribution?, Q. J. Roy. Meteor. Soc., 131, 525–543, https://doi.org/10.1256/qj.03.222, 2005. a
Charlton-Perez, A. J., Ferranti, L., and Lee, R. W.: The influence of the stratospheric state on North Atlantic weather regimes, Q. J. Roy. Meteor. Soc., 144, 1140–1151, https://doi.org/10.1002/qj.3280, 2018. a
Charney, J. G. and Drazin, P. G.: Propagation of planetary-scale disturbances from the lower into the upper atmosphere, J. Geophys. Res., 66, 83–109, https://doi.org/10.1029/JZ066i001p00083, 1961. a, b, c, d
Charron, M., Polavarapu, S., Buehner, M., Vaillancourt, P. A., Charette, C., Roch, M., Morneau, J., Garand, L., Aparicio, J. M., MacPherson, S., Pellerin, S., St-James, J., and Heilliette, S.: The Stratospheric extension of the Canadian global deterministic medium-range weather forecasting system and its impact on tropospheric forecasts, Mon. Weather Rev., 140, 1924–1944, https://doi.org/10.1175/MWR-D-11-00097.1, 2012. a
Chipperfield, M. P., Cariolle, D., Simon, P., Ramaroson, R., and Lary, D. J.: A three-dimensional modeling study of trace species in the Arctic lower stratosphere during winter 1989–1990, J. Geophys. Res.-Atmos., 98, 7199–7218, https://doi.org/10.1029/92JD02977, 1993. a
Christiansen, B.: Stratospheric vacillations in a general circulation model, J. Atmos. Sci., 56, 1858–1872, https://doi.org/10.1175/1520-0469(1999)056<1858:SVIAGC>2.0.CO;2, 1999. a
Christiansen, B., Yang, S., and Madsen, M. S.: Do strong warm ENSO events control the phase of the stratospheric QBO?, Geophys. Res. Lett., 43, 10,489–10,495, https://doi.org/10.1002/2016GL070751, 2016. a
Cohen, J. and Jones, J.: Tropospheric precursors and stratospheric warmings, J. Climate, 24, 6562–6572, https://doi.org/10.1175/2011JCLI4160.1, 2011. a
Committee on Extension of Standard Atmosphere (COSEA): US Standard Atmosphere, 1976, US Government Printing Office, Washington, DC, 1976. a
Coy, L., Wargan, K., Molod, A. M., McCarty, W. R., and Pawson, S.: Structure and dynamics of the quasi-biennial oscillation in MERRA-2, J. Climate, 29, 5339–5354, https://doi.org/10.1175/JCLI-D-15-0809.1, 2016. a
Coy, L., Newman, P. A., Pawson, S., and Lait, L. R.: Dynamics of the disrupted 2015/16 quasi-biennial oscillation, J. Climate, 30, 5661–5674, https://doi.org/10.1175/JCLI-D-16-0663.1, 2017. a
Coy, L., Newman, P. A., Strahan, S., and Pawson, S.: Seasonal variation of the quasi-biennial oscillation descent, J. Geophys. Res.-Atmos., 125, e2020JD033077, https://doi.org/10.1029/2020JD033077, 2020. a
Coy, L., Newman, P. A., Molod, A., Pawson, S., Alexander, M. J., and Holt, L.: Seasonal prediction of the quasi-biennial oscillation, J. Geophys. Res.-Atmos., 127, e2021JD036124, https://doi.org/10.1029/2021JD036124, 2022. a, b
Craig, R. A. and Hering, W. S.: The stratospheric warming of January-February 1957, J. Atmos. Sci., 16, 91–107, https://doi.org/10.1175/1520-0469(1959)016<0091:TSWOJF>2.0.CO;2, 1959. a
de la Cámara, A., Albers, J. R., Birner, T., Garcia, R. R., Hitchcock, P., Kinnison, D. E., and Smith, A. K.: Sensitivity of sudden stratospheric warmings to previous stratospheric conditions, J. Atmos. Sci., 74, 2857–2877, https://doi.org/10.1175/JAS-D-17-0136.1, 2017. a
Dee, D. P., Uppala, S. M., Simmons, A. J., Berrisford, P., Poli, P., Kobayashi, S., Andrae, U., Balmaseda, M. A., Balsamo, G., Bauer, P., Bechtold, P., Beljaars, A. C. M., van de Berg, L., Bidlot, J., Bormann, N., Delsol, C., Dragani, R., Fuentes, M., Geer, A. J., Haimberger, L., Healy, S. B., Hersbach, H., Hólm, E. V., Isaksen, L., Kållberg, P., Köhler, M., Matricardi, M., McNally, A. P., Monge-Sanz, B. M., Morcrette, J.-J., Park, B.-K., Peubey, C., de Rosnay, P., Tavolato, C., Thépaut, J.-N., and Vitart, F.: The ERA-Interim reanalysis: configuration and performance of the data assimilation system, Q. J. Roy. Meteor. Soc., 137, 553–597, https://doi.org/10.1002/qj.828, 2011. a, b, c, d
Dickinson, R. E.: Planetary Rossby waves propagating vertically through weak westerly wind wave-guides, J. Atmos. Sci., 25, 984–1002, https://doi.org/10.1175/1520-0469(1968)025<0984:PRWPVT>2.0.CO;2, 1968. a
Dobson, G. M. B., Harrison, D. N., and Lawrence, J.: Measurements of the amount of ozone in the Earth’s atmosphere and its relation to other geophysical conditions, P. R. Soc. A, 122, 456–486, https://doi.org/10.1098/rspa.1929.0034, 1929. a
Domeisen, D. and Butler, A.: Stratospheric drivers of extreme events at the Earth’s surface, Commun. Earth Environ., 1, 59, https://doi.org/10.1038/s43247-020-00060-z, 2020. a, b, c, d
Domeisen, D. I. V.: Estimating the frequency of sudden stratospheric warming events from surface observations of the North Atlantic oscillation, J. Geophys. Res.-Atmos., 124, 3180–3194, https://doi.org/10.1029/2018JD030077, 2019. a, b, c
Domeisen, D. I. V., Butler, A. H., Charlton-Perez, A. J., Ayarzagüena, B., Baldwin, M. P., Dunn-Sigouin, E., Furtado, J. C., Garfinkel, C. I., Hitchcock, P., Karpechko, A. Y., Kim, H., Knight, J., Lang, A. L., Lim, E.-P., Marshall, A., Roff, G., Schwartz, C., Simpson, I. R., Son, S.-W., and Taguchi, M.: The role of the stratosphere in subseasonal to seasonal prediction: 2. Predictability arising from stratosphere-troposphere coupling, J. Geophys. Res.-Atmos., 125, e2019JD030923, https://doi.org/10.1029/2019JD030923, 2020a. a, b
Domeisen, D. I. V., Butler, A. H., Charlton-Perez, A. J., Ayarzagüena, B., Baldwin, M. P., Dunn-Sigouin, E., Furtado, J. C., Garfinkel, C. I., Hitchcock, P., Karpechko, A. Y., Kim, H., Knight, J., Lang, A. L., Lim, E.-P., Marshall, A., Roff, G., Schwartz, C., Simpson, I. R., Son, S.-W., and Taguchi, M.: The role of the stratosphere in subseasonal to seasonal prediction: 1. Predictability of the stratosphere, J. Geophys. Res.-Atmos., 125, e2019JD030920, https://doi.org/10.1029/2019JD030920, 2020b. a, b, c, d
Dunkerton, T.: On the mean meridional mass motions of the stratosphere and mesosphere, J. Atmos. Sci., 35, 2325–2333, https://doi.org/10.1175/1520-0469(1978)035<2325:OTMMMM>2.0.CO;2, 1978. a, b
Dunkerton, T. J.: Laterally‐propagating Rossby waves in the easterly acceleration phase of the quasi‐biennial oscillation, Atmosphere-Ocean, 21, 55–68, https://doi.org/10.1080/07055900.1983.9649155, 1983. a
Dunkerton, T. J.: Nonlinear propagation of zonal winds in an atmosphere with Newtonian cooling and equatorial wave driving, J. Atmos. Sci., 48, 236–263, https://doi.org/10.1175/1520-0469(1991)048<0236:NPOZWI>2.0.CO;2, 1991. a
Dunkerton, T. J.: The role of gravity waves in the quasi-biennial oscillation, J. Geophys. Res.-Atmos., 102, 26053–26076, https://doi.org/10.1029/96JD02999, 1997. a
Dunkerton, T. J.: The quasi-biennial oscillation of 2015–2016: hiccup or death spiral?, Geophys. Res. Lett., 43, 10547–10552, https://doi.org/10.1002/2016GL070921, 2016. a
Dunstone, N., Smith, D., Scaife, A. A., Hermanson, L., Eade, R., Robinson, N., Andrews, M., and Knight, J.: Skillful predictions of the winter North Atlantic Oscillation one year ahead, Nat. Geosci., 9, 809–814, https://doi.org/10.1038/ngeo2824, 2016. a
Ebdon, R. A.: The quasi-biennial oscillation and its association with tropospheric circulation patterns, Meteorol. Mag., 104, 282–297, 1975. a
Ebdon, R. A. and Veryard, R. G.: Fluctuations in equatorial stratospheric winds, Nature, 189, 791–793, https://doi.org/10.1038/189791a0, 1961. a, b
Eliassen, A. and Palm, E.: On the transfer of energy in stationary mountain waves, Geofysiske Publikasjoner, 22, 1–23, 1961. a, b
Elsbury, D., Peings, Y., and Magnusdottir, G.: CMIP6 models underestimate the Holton-Tan effect, Geophys. Res. Lett., 48, e2021GL094083, https://doi.org/10.1029/2021GL094083, 2021. a
English, S. J., Renshaw, R. J., Dibben, P. C., Smith, A. J., Rayer, P. J., Poulsen, C., Saunders, F. W., and Eyre, J. R.: A comparison of the impact of TOVS arid ATOVS satellite sounding data on the accuracy of numerical weather forecasts, Q. J. Roy. Meteor. Soc., 126, 2911–2931, https://doi.org/10.1002/qj.49712656915, 2000. a
European Centre for Medium-Range Weather Forecasts: ERA-Interim reanalysis data, ECMWF [data set], https://apps.ecmwf.int/datasets/data/interim-full-daily/levtype=sfc/, last access: 3 November 2022. a
Eyring, V., Butchart, N., Waugh, D. W., Akiyoshi, H., Austin, J., Bekki, S., Bodeker, G. E., Boville, B. A., Brühl, C., Chipperfield, M. P., Cordero, E., Dameris, M., Deushi, M., Fioletov, V. E., Frith, S. M., Garcia, R. R., Gettelman, A., Giorgetta, M. A., Grewe, V., Jourdain, L., Kinnison, D. E., Mancini, E., Manzini, E., Marchand, M., Marsh, D. R., Nagashima, T., Newman, P. A., Nielsen, J. E., Pawson, S., Pitari, G., Plummer, D. A., Rozanov, E., Schraner, M., Shepherd, T. G., Shibata, K., Stolarski, R. S., Struthers, H., Tian, W., and Yoshiki, M.: Assessment of temperature, trace species, and ozone in chemistry-climate model simulations of the recent past, J. Geophys. Res.-Atmos., 111, D22308, https://doi.org/10.1029/2006JD007327, 2006. a
Eyring, V., Gleckler, P. J., Heinze, C., Stouffer, R. J., Taylor, K. E., Balaji, V., Guilyardi, E., Joussaume, S., Kindermann, S., Lawrence, B. N., Meehl, G. A., Righi, M., and Williams, D. N.: Towards improved and more routine Earth system model evaluation in CMIP, Earth Syst. Dynam., 7, 813–830, https://doi.org/10.5194/esd-7-813-2016, 2016. a
Farman, J., Gardiner, B., and Shanklin, J.: Large losses of total ozone in Antarctica reveal seasonal ClONOx interaction., Nature, 315, 207–210, https://doi.org/10.1038/315207a0, 1985. a
Fels, S. B., Mahlman, J. D., Schwarzkopf, M. D., and Sinclair, R. W.: Stratospheric sensitivity to perturbations in ozone and carbon dioxide: radiative and dynamical response, J. Atmos. Sci., 37, 2265–2297, https://doi.org/10.1175/1520-0469(1980)037<2265:SSTPIO>2.0.CO;2, 1980. a
Feser, F., Graf, H. F., and Perlwitz, J.: Secular variability of the coupled tropospheric and stratospheric circulation in the GCM ECHAM 3/LSG, Theor. Appl. Climatol., 65, 1–15, https://doi.org/10.1007/s007040050001, 2000. a
Funk, J. P. and Garnham, G. L.: Australian ozone observations and a suggested 24 month cycle, Tellus, 14, 378–382, https://doi.org/10.1111/j.2153-3490.1962.tb01350.x, 1962. a
Garfinkel, C. I. and Hartmann, D. L.: Effects of the El Niño–southern oscillation and the quasi-biennial oscillation on polar temperatures in the stratosphere, J. Geophys. Res.-Atmos., 112, D19112, https://doi.org/10.1029/2007JD008481, 2007. a
Garfinkel, C. I., Shaw, T. A., Hartmann, D. L., and Waugh, D. W.: Does the Holton-Tan mechanism explain how the quasi-biennial oscillation modulates the Arctic polar vortex?, J. Atmos. Sci., 69, 1713–1733, https://doi.org/10.1175/JAS-D-11-0209.1, 2012. a
Garfinkel, C. I., Schwartz, C., White, I. P., and Rao, J.: Predictability of the early winter Arctic oscillation from autumn Eurasian snow cover in subseasonal forecast models, Clim. Dynam., 55, 961–974, https://doi.org/10.1007/s00382-020-05305-3, 2020a. a
Garfinkel, C. I., White, I., Gerber, E. P., Jucker, M., and Erez, M.: The building blocks of Northern Hemisphere wintertime stationary waves, J. Climate, 33, 5611–5633, https://doi.org/10.1175/JCLI-D-19-0181.1, 2020b. a
Garfinkel, C. I., Gerber, E. P., Shamir, O., Rao, J., Jucker, M., White, I., and Paldor, N.: A QBO cookbook: sensitivity of the quasi-biennial oscillation to resolution, resolved waves, and parameterized gravity waves, J. Adv. Model. Earth Sy., 14, e2021MS002568, https://doi.org/10.1029/2021MS002568, 2022. a
Garreaud, R.: Record-breaking climate anomalies lead to severe drought and environmental disruption in western Patagonia in 2016, Clim. Res., 74, 217–229, https://doi.org/10.3354/cr01505, 2018. a
Gelaro, R., McCarty, W., Suárez, M. J., Todling, R., Molod, A., Takacs, L., Randles, C. A., Darmenov, A., Bosilovich, M. G., Reichle, R., Wargan, K., Coy, L., Cullather, R., Draper, C., Akella, S., Buchard, V., Conaty, A., da Silva, A. M., Gu, W., Kim, G.-K., Koster, R., Lucchesi, R., Merkova, D., Nielsen, J. E., Partyka, G., Pawson, S., Putman, W., Rienecker, M., Schubert, S. D., Sienkiewicz, M., and Zhao, B.: The Modern-Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2), J. Climate, 30, 5419–5454, https://doi.org/10.1175/JCLI-D-16-0758.1, 2017. a, b
Gerber, E. P. and Manzini, E.: The Dynamics and Variability Model Intercomparison Project (DynVarMIP) for CMIP6: assessing the stratosphere–troposphere system, Geosci. Model Dev., 9, 3413–3425, https://doi.org/10.5194/gmd-9-3413-2016, 2016. a
Gerber, E. P. and Martineau, P.: Quantifying the variability of the annular modes: reanalysis uncertainty vs. sampling uncertainty, Atmos. Chem. Phys., 18, 17099–17117, https://doi.org/10.5194/acp-18-17099-2018, 2018. a
Gerber, E. P., Butler, A., Calvo, N., Charlton-Perez, A., Giorgetta, M., Manzini, E., Perlwitz, J., Polvani, L. M., Sassi, F., Scaife, A. A., Shaw, T. A., Son, S.-W., and Watanabe, S.: Assessing and understanding the impact of stratospheric dynamics and variability on the Earth system, B. Am. Meteorol. Soc., 93, 845–859, https://doi.org/10.1175/BAMS-D-11-00145.1, 2012. a
Gillett, N. P., Kell, T. D., and Jones, P. D.: Regional climate impacts of the Southern Annular Mode, Geophys. Res. Lett., 33, L23704, https://doi.org/10.1029/2006GL027721, 2006. a
Goss, M., Lindgren, E. A., Sheshadri, A., and Diffenbaugh, N. S.: The Atlantic jet response to stratospheric events: a regime perspective, J. Geophys. Res.-Atmos., 126, e2020JD033358, https://doi.org/10.1029/2020JD033358, 2021. a
Gray, L. J., Scaife, A. A., Mitchell, D. M., Osprey, S., Ineson, S., Hardiman, S., Butchart, N., Knight, J., Sutton, R., and Kodera, K.: A lagged response to the 11 year solar cycle in observed winter Atlantic/European weather patterns, J. Geophys. Res.-Atmos., 118, 13,405–13,420, https://doi.org/10.1002/2013JD020062, 2013. a
Gray, W. M.: Atlantic seasonal hurricane frequency. Part I: El Niño and 30 mb quasi-biennial oscillation influences, Mon. Weather Rev., 112, 1649–1668, https://doi.org/10.1175/1520-0493(1984)112<1649:ASHFPI>2.0.CO;2, 1984. a
Hall, R. J., Mitchell, D. M., Seviour, W. J. M., and Wright, C. J.: Tracking the stratosphere-to-surface impact of sudden stratospheric warmings, J. Geophys. Res.-Atmos., 126, e2020JD033881, https://doi.org/10.1029/2020JD033881, 2021a. a, b, c
Hall, R. J., Mitchell, D. M., Seviour, W. J. M., and Wright, C. J.: Persistent model biases in the CMIP6 representation of stratospheric polar vortex variability, J. Geophys. Res.-Atmos., 126, e2021JD034759, https://doi.org/10.1029/2021JD034759, 2021b. a, b
Hamilton, K.: Interannual variability in the Northern Hemisphere winter middle atmosphere in control and perturbed experiments with the GFDL SKYHI general circulation model., J. Atmos. Sci., 52, 44–66, https://doi.org/10.1175/1520-0469(1995)052<0044:IVITNH>2.0.CO;2, 1995. a
Hamilton, K., Wilson, R. J., and Hemler, R.: Middle atmosphere simulated with high vertical and horizontal resolution versions of a GCM: Improvement in the cold pole bias and generation of a QBO-like oscillation in the tropics, J. Atmos. Sci., 56, 3829–3846, https://doi.org/10.1175/1520-0469(1999)056<3829:MASWHV>2.0.CO;2, 1999. a, b
Hamilton, K., Hertzog, A., Vial, F., and Stenchikov, G.: Longitudinal variation of the stratospheric quasi-biennial oscillation, J. Atmos. Sci., 61, 383–402, https://doi.org/10.1175/1520-0469(2004)061<0383:LVOTSQ>2.0.CO;2, 2004. a
Hampson, J. and Haynes, P.: Phase alignment of the tropical stratospheric QBO in the annual cycle, J. Atmos. Sci., 61, 2627–2637, https://doi.org/10.1175/JAS3276.1, 2004. a
Hardiman, S. C., Kushner, P. J., and Cohen, J.: Investigating the ability of general circulation models to capture the effects of Eurasian snow cover on winter climate, J. Geophys. Res.-Atmos., 113, D21123, https://doi.org/10.1029/2008JD010623, 2008. a
Hardiman, S. C., Butchart, N., Charlton-Perez, A. J., Shaw, T. A., Akiyoshi, H., Baumgaertner, A., Bekki, S., Braesicke, P., Chipperfield, M., Dameris, M., Garcia, R. R., Michou, M., Pawson, S., Rozanov, E., and Shibata, K.: Improved predictability of the troposphere using stratospheric final warmings, J. Geophys. Res.-Atmos., 116, D18113, https://doi.org/10.1029/2011JD015914, 2011. a
Hardiman, S. C., Butchart, N., Hinton, T. J., Osprey, S. M., and Gray, L. J.: The effect of a well-resolved stratosphere on surface climate: differences between CMIP5 simulations with high and low top versions of the Met Office climate model, J. Climate, 25, 7083–7099, https://doi.org/10.1175/JCLI-D-11-00579.1, 2012. a
Hardiman, S. C., Scaife, A. A., Dunstone, N. J., and Wang, L.: Subseasonal vacillations in the winter stratosphere, Geophys. Res. Lett., 47, e2020GL087766, https://doi.org/10.1029/2020GL087766, 2020. a, b
Hatfield, L. A. and Scott, R. K.: Internal interannual variability of the winter polar vortex in a simple model of the seasonally evolving stratosphere, Q. J. Roy. Meteor. Soc., 145, 3057–3073, https://doi.org/10.1002/qj.3604, 2019. a
Haynes, P., Hitchcock, P., Hitchman, M., Yoden, S., Hendon, H., Kiladis, G., Kodera, K., and Simpson, I.: The influence of the stratosphere on the tropical troposphere, J. Meteorol. Soc. Jpn., 99, 803–845, https://doi.org/10.2151/jmsj.2021-040, 2021. a, b, c, d, e, f, g, h, i, j
Haynes, P. H. and Shepherd, T. G.: The importance of surface-pressure changes in the response of the atmosphere to zonally-symmetric thermal and mechanical forcing, Q. J. Roy. Meteor. Soc., 115, 1181–1208, https://doi.org/10.1002/qj.49711549002, 1989. a
Haynes, P. H., McIntyre, M. E., Shepherd, T. G., Marks, C. J., and Shine, K. P.: On the “downward control” of extratropical diabatic circulations by eddy-induced mean zonal forces, J. Atmos. Sci., 48, 651–678, https://doi.org/10.1175/1520-0469(1991)048<0651:OTCOED>2.0.CO;2, 1991. a, b, c, d
Held, I. M.: 100 years of progress in understanding the general circulation of the atmosphere, Meteor. Mon., 59, 6.1–6.23, https://doi.org/10.1175/AMSMONOGRAPHS-D-18-0017.1, 2019. a
Held, I. M., Ting, M., and Wang, H.: Northern winter stationary waves: Theory and modeling, J. Climate, 15, 2125–2144, https://doi.org/10.1175/1520-0442(2002)015<2125:NWSWTA>2.0.CO;2, 2002. a
Hersbach, H., Bell, B., Berrisford, P., Biavati, G., Horányi, A., Muñoz Sabater, J., Nicolas, J., Peubey, C., Radu, R., Rozum, I., Schepers, D., Simmons, A., Soci, C., Dee, D., and Thépaut, J.-N.: ERA5 hourly data on single levels from 1959 to present, Copernicus Climate Change Service (C3S) Climate Data Store (CDS) [data set], https://doi.org/10.24381/cds.adbb2d47, 2018. a
Hersbach, H., Bell, B., Berrisford, P., Hirahara, S., Horányi, A., Muñoz Sabater, J., Nicolas, J., Peubey, C., Radu, R., Schepers, D., Simmons, A., Soci, C., Abdalla, S., Abellan, X., Balsamo, G., Bechtold, P., Biavati, G., Bidlot, J., Bonavita, M., De Chiara, G., Dahlgren, P., Dee, D., Diamantakis, M., Dragani, R., Flemming, J., Forbes, R., Fuentes, M., Geer, A., Haimberger, L., Healy, S., Hogan, R. J., Hólm, E., Janisková, M., Keeley, S., Laloyaux, P., Lopez, P., Lupu, C., Radnoti, G., de Rosnay, P., Rozum, I., Vamborg, F., Villaume, S., and Thépaut, J.-N.: The ERA5 global reanalysis, Q. J. Roy. Meteor. Soc., 146, 1999–2049, https://doi.org/10.1002/qj.3803, 2020. a, b, c, d
Hertzog, A.: How can we improve the driving of the quasi-biennial oscillation in climate models?, J. Geophys. Res.-Atmos., 125, e2020JD033411, https://doi.org/10.1029/2020JD033411, 2020. a
Hitchcock, P. and Haynes, P. H.: Stratospheric control of planetary waves, Geophys. Res. Lett., 43, 11,884–11,892, https://doi.org/10.1002/2016GL071372, 2016. a
Hitchcock, P. and Simpson, I. R.: The downward influence of stratospheric sudden warmings, J. Atmos. Sci., 71, 3856–3876, https://doi.org/10.1175/JAS-D-14-0012.1, 2014. a
Hitchcock, P. and Simpson, I. R.: Quantifying eddy feedbacks and forcings in the tropospheric response to stratospheric sudden warmings, J. Atmos. Sci., 73, 3641–3657, https://doi.org/10.1175/JAS-D-16-0056.1, 2016. a
Hitchcock, P., Haynes, P. H., Randel, W. J., and Birner, T.: The emergence of shallow easterly jets within QBO westerlies, J. Atmos. Sci., 75, 21–40, https://doi.org/10.1175/JAS-D-17-0108.1, 2018. a
Hitchman, M. H., Yoden, S., Haynes, P. H., Kumar, V., and Tegtmeir, S.: An observational history of the direct influence of the stratospheric quasi-biennial oscillation on the tropical and subtropical upper troposphere and lower stratosphere, J. Meteorol. Soc. Jpn., 99, 239–267, https://doi.org/10.2151/jmsj.2021-012, 2021. a
Ho, C.-H., Kim, H.-S., Jeong, J.-H., and Son, S.-W.: Influence of stratospheric quasi-biennial oscillation on tropical cyclone tracks in the western North Pacific, Geophys. Res. Lett., 36, L06702, https://doi.org/10.1029/2009GL037163, 2009. a
Holt, L. A., Lott, F., Garcia, R. R., Kiladis, G. N., Cheng, Y.-M., Anstey, J. A., Braesicke, P., Bushell, A. C., Butchart, N., Cagnazzo, C., Chen, C.-C., Chun, H.-Y., Kawatani, Y., Kerzenmacher, T., Kim, Y.-H., McLandress, C., Naoe, H., Osprey, S., Richter, J. H., Scaife, A. A., Scinocca, J., Serva, F., Versick, S., Watanabe, S., Yoshida, K., and Yukimoto, S.: An evaluation of tropical waves and wave forcing of the QBO in the QBOi models, Q. J. Roy. Meteor. Soc., 148, 1541–1567, https://doi.org/10.1002/qj.3827, 2022. a
Holton, J. R. and Lindzen, R. S.: An updated theory for the quasi-biennial cycle of the tropical stratosphere, J. Atmos. Sci., 29, 1076–1080, https://doi.org/10.1175/1520-0469(1972)029<1076:AUTFTQ>2.0.CO;2, 1972. a, b
Holton, J. R. and Mass, C.: Stratospheric vacillation cycles, J. Atmos. Sci., 33, 2218–2225, https://doi.org/10.1175/1520-0469(1976)033<2218:SVC>2.0.CO;2, 1976. a
Holton, J. R. and Tan, H. C.: The influence of the equatorial quasi-biennial oscillation on the global circulation at 50 mb, J. Atmos. Sci., 37, 2200–2207, https://doi.org/10.1175/1520-0469(1980)037<2200:TIOTEQ>2.0.CO;2, 1980. a, b, c
Horinouchi, T. and Yoden, S.: Wave–mean flow interaction associated with a QBO-like oscillation simulated in a simplified GCM, J. Atmos. Sci., 55, 502–526, https://doi.org/10.1175/1520-0469(1998)055<0502:WMFIAW>2.0.CO;2, 1998. a
Hoskins, B. J., McIntyre, M. E., and Robertson, A. W.: On the use and significance of isentropic potential vorticity maps, Q. J. R. Meteorol. Soc., 111, 877–946, https://doi.org/10.1002/qj.49711147002, 1985. a
Ichimaru, T., Noguchi, S., Hirooka, T., and Mukougawa, H.: Predictability changes of stratospheric circulations in Northern Hemisphere winter, J. Meteorol. Soc. Jpn., 94, 7–24, https://doi.org/10.2151/jmsj.2016-001, 2016. a
Ineson, S. and Scaife, A. A.: The role of the stratosphere in the European climate response to El Niño, Nat. Geosci., 2, 32–36, https://doi.org/10.1038/ngeo381, 2009. a
Jia, L., Yang, X., Vecchi, G., Gudgel, R., Delworth, T., Fueglistaler, S., Lin, P., Scaife, A. A., Underwood, S., and Lin, S.-J.: Seasonal prediction skill of northern extratropical surface temperature driven by the stratosphere, J. Climate, 30, 4463–4475, https://doi.org/10.1175/JCLI-D-16-0475.1, 2017. a
Jucker, M.: Scaling of Eliassen-Palm flux vectors, Atmos. Sci. Lett., 22, e1020, https://doi.org/10.1002/asl.1020, 2021. a
Jucker, M. and Gerber, E. P.: Untangling the annual cycle of the tropical tropopause layer with an idealized moist model, J. Climate, 30, 7339–7358, https://doi.org/10.1175/JCLI-D-17-0127.1, 2017. a
Jucker, M., Reichler, T., and Waugh, D. W.: How frequent are Antarctic sudden stratospheric warmings in present and future climate?, Geophys. Res. Lett., 48, e2021GL093215, https://doi.org/10.1029/2021GL093215, 2021. a
Kang, M.-J. and Chun, H.-Y.: Contributions of equatorial waves and small-scale convective gravity waves to the 2019/20 quasi-biennial oscillation (QBO) disruption, Atmos. Chem. Phys., 21, 9839–9857, https://doi.org/10.5194/acp-21-9839-2021, 2021. a
Kang, M.-J., Chun, H.-Y., and Garcia, R. R.: Role of equatorial waves and convective gravity waves in the 2015/16 quasi-biennial oscillation disruption, Atmos. Chem. Phys., 20, 14669–14693, https://doi.org/10.5194/acp-20-14669-2020, 2020. a
Karpechko, A. Y.: Predictability of sudden stratospheric warmings in the ECMWF extended-range forecast system, Mon. Weather Rev., 146, 1063–1075, https://doi.org/10.1175/MWR-D-17-0317.1, 2018. a
Karpechko, A. Y., Hitchcock, P., Peters, D. H. W., and Schneidereit, A.: Predictability of downward propagation of major sudden stratospheric warmings, Q. J. Roy. Meteor. Soc., 143, 1459–1470, https://doi.org/10.1002/qj.3017, 2017. a
Karpechko, A. Y., Tyrrell, N. L., and Rast, S.: Sensitivity of QBO teleconnection to model circulation biases, Q. J. Roy. Meteor. Soc., 147, 2147–2159, https://doi.org/10.1002/qj.4014, 2021. a, b
Kasahara, A. and Sasamori, T.: Simulation experiments with a 12-layer stratospheric global circulation model. II. Momentum balance and energetics in the stratosphere, J. Atmos. Sci., 31, 408–422, https://doi.org/10.1175/1520-0469(1974)031<0408:SEWALS>2.0.CO;2, 1974. a
Kawatani, Y. and Hamilton, K.: Weakened stratospheric quasi-biennial oscillation driven by increased tropical mean upwelling, Nature, 497, 478–481, https://doi.org/10.1038/nature12140, 2013. a
Kawatani, Y., Hamilton, K., Gray, L. J., Osprey, S. M., Watanabe, S., and Yamashita, Y.: The effects of a well-resolved stratosphere on the simulated boreal winter circulation in a climate model, J. Atmos. Sci., 76, 1203–1226, https://doi.org/10.1175/JAS-D-18-0206.1, 2019. a
Kawatani, Y., Hirooka, T., Hamilton, K., Smith, A. K., and Fujiwara, M.: Representation of the equatorial stratopause semiannual oscillation in global atmospheric reanalyses, Atmos. Chem. Phys., 20, 9115–9133, https://doi.org/10.5194/acp-20-9115-2020, 2020. a
Keegan, T. J.: Large-scale disturbances of atmospheric circulation between 30 and 70 kilometers in winter, J. Geophys. Res., 67, 1831–1838, https://doi.org/10.1029/JZ067i005p01831, 1962. a
Kidston, J., Scaife, A. A., Hardiman, S. C., Mitchell, D. M., Butchart, N., Baldwin, M. P., and Gray, L. J.: Stratospheric influence on tropospheric jet streams, storm tracks and surface weather, Nat. Geosci., 8, 433–440, https://doi.org/10.1038/ngeo2424, 2015. a, b, c, d, e, f, g, h, i
Kim, B.-M., Son, S.-W., Min, S.-K., Jeong, J.-H., Kim, S.-J., Zhang, X., Shim, T., and Yoon, J.-H.: Weakening of the stratospheric polar vortex by Arctic sea-ice loss, Nat. Commun., 5, 1–8, https://doi.org/10.1038/ncomms5646, 2014. a
Kim, H., Son, S.-W., and Yoo, C.: QBO modulation of the MJO-related precipitation in East Asia, J. Geophys. Res.-Atmos., 125, e2019JD031929, https://doi.org/10.1029/2019JD031929, 2020. a
King, A. D., Butler, A. H., Jucker, M., Earl, N. O., and Rudeva, I.: Observed relationships between sudden stratospheric warmings and European climate extremes, J. Geophys. Res.-Atmos., 124, 13943–13961, https://doi.org/10.1029/2019JD030480, 2019. a
Klotzbach, P., Abhik, S., Hendon, H. H., Bell, M., Lucas, C., Marshall, A. G., and Oliver, E. C. J.: On the emerging relationship between the stratospheric quasi-biennial oscillation and the Madden-Julian oscillation, Sci. Rep., 9, 2981, https://doi.org/10.1038/s41598-019-40034-6, 2019. a, b
Kodera, K.: Influence of stratospheric sudden warming on the equatorial troposphere, Geophys. Res. Lett., 33, L06804, https://doi.org/10.1029/2005GL024510, 2006. a
Kodera, K. and Yamada, K.: Impact of the SH major stratospheric warming on the Hadley circulation: A case study, Pap. Meteorol. Geophys., 54, 111–116, https://doi.org/10.2467/mripapers.54.111, 2004. a
Kodera, K., Yamazaki, K., Chiba, K., and Shibata, K.: Downward propagation of upper stratospheric mean zonal wind perturbation to the troposphere, Geophys. Res. Lett., 17, 1263–1266, https://doi.org/10.1029/GL017i009p01263, 1990. a
Kodera, K., Mukougawa, H., and Kuroda, Y.: A general circulation model study of the impact of a stratospheric sudden warming event on tropical convection, SOLA, 7, 197–200, https://doi.org/10.2151/sola.2011-050, 2011. a
Kretschmer, M., Zappa, G., and Shepherd, T. G.: The role of Barents–Kara sea ice loss in projected polar vortex changes, Weather Clim. Dynam., 1, 715–730, https://doi.org/10.5194/wcd-1-715-2020, 2020. a
Kuroda, Y. and Kodera, K.: Interannual variability in the troposphere and stratosphere of the Southern Hemisphere winter, J. Geophys. Res.-Atmos., 103, 13787–13799, https://doi.org/10.1029/98JD01042, 1998. a
Kuroda, Y. and Kodera, K.: Variability of the polar night jet in the Northern and Southern Hemispheres, J. Geophys. Res.-Atmos., 106, 20703–20713, https://doi.org/10.1029/2001JD900226, 2001. a
Labitzke, K.: On the interannual variability of the middle stratosphere during the northern winters, J. Meteorol. Soc. Jpn., 60, 124–139, https://doi.org/10.2151/jmsj1965.60.1_124, 1982. a
Lahoz, W. A.: Predictive skill of the UKMO unified model in the lower stratosphere, Q. J. Roy. Meteor. Soc., 125, 2205–2238, https://doi.org/10.1002/qj.49712555813, 1999. a
Larson, E. J. L., Portmann, R. W., Rosenlof, K. H., Fahey, D. W., Daniel, J. S., and Ross, M. N.: Global atmospheric response to emissions from a proposed reusable space launch system, Earth's Future, 5, 37–48, https://doi.org/10.1002/2016EF000399, 2017. a
Leovy, C. B.: Simple models of thermally driven mesospheric circulation, J. Atmos. Sci., 21, 327–341, https://doi.org/10.1175/1520-0469(1964)021<0327:SMOTDM>2.0.CO;2, 1964. a
Lim, E.-P., Hendon, H. H., and Thompson, D. W. J.: Seasonal evolution of stratosphere-troposphere coupling in the Southern Hemisphere and implications for the predictability of surface climate, J. Geophys. Res.-Atmos., 123, 12002–12016, https://doi.org/10.1029/2018JD029321, 2018. a, b
Lim, E.-P., Hendon, H. H., Boschat, G., Hudson, D., Thompson, D. W. J., Dowdy, A. J., and Arblaster, J. M.: Australian hot and dry extremes induced by weakenings of the stratospheric polar vortex, Nat. Geosci., 12, 896–901, https://doi.org/10.1038/s41561-019-0456-x, 2019a. a
Lim, E.-P., Hendon, H. H., Butler, A. H., Thompson, D. W. J., Lawrence, Z. D., Scaife, A. A., Shepherd, T. G., Polichtchouk, I., Nakamura, H., Kobayashi, C., Comer, R., Coy, L., Dowdy, A., Garreaud, R. D., Newman, P. A., and Wang, G.: The 2019 Southern Hemisphere stratospheric polar vortex weakening and its impacts, B. American Meteorol. Soc., 102, E1150–E1171, https://doi.org/10.1175/BAMS-D-20-0112.1, 2021. a
Lim, Y., Son, S.-W., Marshall, A. G., Hendon, H. H., and Seo, K.-H.: Influence of the QBO on MJO prediction skill in the subseasonal-to-seasonal prediction models, Clim. Dynam., 53, 1681–1695, https://doi.org/10.1007/s00382-019-04719-y, 2019b. a, b
Lin, P., Held, I., and Ming, Y.: The early development of the 2015/16 quasi-biennial oscillation disruption, J. Atmos. Sci., 76, 821–836, https://doi.org/10.1175/JAS-D-18-0292.1, 2019. a
Lindzen, R. and Holton, J. R.: A theory of the quasi-biennial oscillation, J. Atmos. Sci., 25, 1095–1107, https://doi.org/10.1175/1520-0469(1968)025<1095:ATOTQB>2.0.CO;2, 1968. a, b, c
Lott, F. and Guez, L.: A stochastic parameterization of the gravity waves due to convection and its impact on the equatorial stratosphere, J. Geophys. Res.-Atmos., 118, 8897–8909, https://doi.org/10.1002/jgrd.50705, 2013. a
Lu, H., Bracegirdle, T. J., Phillips, T., and Turner, J.: A comparative study of wave forcing derived from the ERA-40 and ERA-Interim reanalysis datasets, J. Climate, 28, 2291–2311, https://doi.org/10.1175/JCLI-D-14-00356.1, 2015. a
Ma, T., Chen, W., Huangfu, J., Song, L., and Cai, Q.: The observed influence of the quasi-biennial oscillation in the lower equatorial stratosphere on the East Asian winter monsoon during early boreal winter, Int. J. Climatol., 41, 6254–6269, https://doi.org/10.1002/joc.7192, 2021. a
Manabe, S. and Hunt, B. G.: Experiments with a stratospheric general circulation model I: Radiative and dynamic aspects, Mon. Weather Rev., 96, 477–502, https://doi.org/10.1175/1520-0493(1968)096<0477:EWASGC>2.0.CO;2, 1968. a
Manney, G. L., Schwartz, M. J., Krüger, K., Santee, M. L., Pawson, S., Lee, J. N., Daffer, W. H., Fuller, R. A., and Livesey, N. J.: Aura Microwave Limb Sounder observations of dynamics and transport during the record-breaking 2009 Arctic stratospheric major warming, Geophys. Res. Lett., 36, L12815,, https://doi.org/10.1029/2009GL038586, 2009. a
Manzini, E. and Bengtsson, L.: Stratospheric climate and variability from a general circulation model and observations, Clim. Dynam., 12, 615–639, https://doi.org/10.1007/BF00216270, 1996. a
Manzini, E., McFarlane, N. A., and McLandress, C.: Impact of the Doppler spread parameterization on the simulation of the middle atmosphere circulation using the MA/ECHAM4 general circulation model, J. Geophys. Res.-Atmos., 102, 25751–25762, https://doi.org/10.1029/97JD01096, 1997. a
Manzini, E., Steil, B., Brühl, C., Giorgetta, M. A., and Krüger, K.: A new interactive chemistry-climate model: 2. Sensitivity of the middle atmosphere to ozone depletion and increase in greenhouse gases and implications for recent stratospheric cooling, J. Geophys. Res.-Atmos., 108, 4429, https://doi.org/10.1029/2002JD002977, 2003. a
Manzini, E., Cagnazzo, C., Fogli, P. G., Bellucci, A., and Müller, W. A.: Stratosphere-troposphere coupling at inter-decadal time scales: Implications for the North Atlantic Ocean, Geophys. Res. Lett., 39, L05801, https://doi.org/10.1029/2011GL050771, 2012. a
Marshall, A. G. and Scaife, A. A.: Improved predictability of stratospheric sudden warming events in an atmospheric general circulation model with enhanced stratospheric resolution, J. Geophys. Res.-Atmos., 115, D16114, https://doi.org/10.1029/2009JD012643, 2010. a
Marshall, A. G., Hendon, H. H., Son, S.-W., and Lim, Y.: Impact of the quasi-biennial oscillation on predictability of the Madden–Julian oscillation, Clim. Dynam., 49, 1365–1377, https://doi.org/10.1007/s00382-016-3392-0, 2017. a, b
Martin, Z., Son, S.-W., Butler, A., Hendon, H., Kim, H., Sobel, A., Yoden, S., and Zhang, C.: The influence of the quasi-biennial oscillation on the Madden–Julian oscillation, Nat. Rev. Earth Environ., 2, 477–489, https://doi.org/10.1038/s43017-021-00173-9, 2021. a, b, c, d
Martius, O., Polvani, L. M., and Davies, H. C.: Blocking precursors to stratospheric sudden warming events, Geophys. Res. Lett., 36, L14806, https://doi.org/10.1029/2009GL038776, 2009. a
Match, A. and Fueglistaler, S.: Mean-flow damping forms the buffer zone of the quasi-biennial oscillation: 1D Theory, J. Atmos. Sci., 77, 1955–1967, https://doi.org/10.1175/JAS-D-19-0293.1, 2020. a
Matsuno, T.: Vertical propagation of stationary planetary waves in the winter Northern Hemisphere, J. Atmos. Sci., 27, 871–883, https://doi.org/10.1175/1520-0469(1970)027<0871:VPOSPW>2.0.CO;2, 1970. a
Matsuno, T.: A dynamical model of the stratospheric sudden warming, J. Atmos. Sci., 28, 1479–1494, https://doi.org/10.1175/1520-0469(1971)028<1479:ADMOTS>2.0.CO;2, 1971. a, b, c
Matthewman, N. J. and Esler, J. G.: Stratospheric sudden warmings as self-tuning resonances. Part I: vortex splitting events, J. Atmos. Sci., 68, 2481–2504, https://doi.org/10.1175/JAS-D-11-07.1, 2011. a
Matthias, V., Stober, G., Kozlovsky, A., Lester, M., Belova, E., and Kero, J.: Vertical structure of the Arctic spring transition in the middle atmosphere, J. Geophys. Res.-Atmos., 126, e2020JD034353, https://doi.org/10.1029/2020JD034353, 2021. a
Maycock, A. C. and Hitchcock, P.: Do split and displacement sudden stratospheric warmings have different annular mode signatures?, Geophys. Res. Lett., 42, 10943–10951, https://doi.org/10.1002/2015GL066754, 2015. a
Maycock, A. C., Masukwedza, G. I. T., Hitchcock, P., and Simpson, I. R.: A regime perspective on the North Atlantic eddy-driven jet response to sudden stratospheric warmings, J. Climate, 33, 3901–3917, https://doi.org/10.1175/JCLI-D-19-0702.1, 2020. a
McElroy, C. T. and Fogal, P. F.: Ozone: From discovery to protection, Atmos. Ocean, 46, 1–13, https://doi.org/10.3137/ao.460101, 2008. a
McIntyre, M. E. and Palmer, T. N.: Breaking planetary waves in the stratosphere, Nature, 305, 593–600, https://doi.org/10.1038/305593a0, 1983. a, b, c, d
McIntyre, M. E. and Palmer, T. N.: The “surf zone” in the stratosphere, J. Atmos. Terr. Phys., 46, 825–849, https://doi.org/10.1016/0021-9169(84)90063-1, 1984. a, b
McLandress, C.: On the importance of gravity waves in the middle atmosphere and their parameterization in general circulation models, J. Atmos. Sol.-Terr. Phy., 60, 1357–1383, https://doi.org/10.1016/S1364-6826(98)00061-3, 1998. a
Mechoso, C. R., Yamazaki, K., Kitoh, A., and Arakawa, A.: Numerical forecasts of stratospheric warming events during the winter of 1979, Mon. Weather Rev., 113, 1015–1030, https://doi.org/10.1175/1520-0493(1985)113<1015:NFOSWE>2.0.CO;2, 1985. a
Miller, D. E., Brownscombe, J. L., Carruthers, G. P., Pick, D. R., Stewart, K. H., Massey, H. S. W., Beynon, W. J. G., Houghton, J. T., and Thomas, L.: Operational temperature sounding of the stratosphere, Philos. T. R. Soc. A, 296, 65–71, https://doi.org/10.1098/rsta.1980.0156, 1980. a
Minzner, R.: The 1976 Standard Atmosphere and its relationship to earlier standards, Rev. Geophys., 15, 375–384, https://doi.org/10.1029/RG015i003p00375, 1977. a
Mitchell, D. M., Charlton-Perez, A. J., and Gray, L. J.: Characterizing the variability and extremes of the stratospheric polar vortices using 2D moment analysis, J. Atmos. Sci., 68, 1194–1213, https://doi.org/10.1175/2010JAS3555.1, 2011. a
Miyakoda, K., Strickler, R. F., and Hembree, G. D.: Numerical simulation of the breakdown of a polar-night vortex in the stratosphere, J. Atmos. Sci., 27, 139–154, https://doi.org/10.1175/1520-0469(1970)027<0139:NSOTBO>2.0.CO;2, 1970. a
Mukougawa, H. and Hirooka, T.: Predictability of stratospheric sudden warming: A case study for 1998/99 winter, Mon. Weather Rev., 132, 1764–1776, https://doi.org/10.1175/1520-0493(2004)132<1764:POSSWA>2.0.CO;2, 2004. a
Murgatroyd, R. J. and Singleton, F.: Possible meridional circulations in the stratosphere and mesosphere, Q. J. Roy. Meteor. Soc., 87, 125–135, https://doi.org/10.1002/qj.49708737202, 1961. a, b, c, d, e, f, g
Naito, Y. and Hirota, I.: Interannual Variability of the Northern Winter Stratospheric Circulation Related to the QBO and the solar cycle, J. Meteorol. Soc. Jpn., 75, 925–937, https://doi.org/10.2151/jmsj1965.75.4_925, 1997. a
Newman, P. A., Nash, E. R., and Rosenfield, J. E.: What controls the temperature of the Arctic stratosphere during the spring?, J. Geophys. Res.-Atmos., 106, 19999–20010, https://doi.org/10.1029/2000JD000061, 2001. a, b, c
Newman, P. A., Coy, L., Pawson, S., and Lait, L. R.: The anomalous change in the QBO in 2015–2016, Geophys. Res. Lett., 43, 8791–8797, https://doi.org/10.1002/2016GL070373, 2016. a, b, c, d, e
Nishimoto, E. and Yoden, S.: Influence of the stratospheric quasi-biennial oscillation on the Madden–Julian oscillation during Austral summer, J. Atmos. Sci., 74, 1105–1125, https://doi.org/10.1175/JAS-D-16-0205.1, 2017. a
Noguchi, S., Mukougawa, H., Kuroda, Y., Mizuta, R., Yabu, S., and Yoshimura, H.: Predictability of the stratospheric polar vortex breakdown: An ensemble reforecast experiment for the splitting event in January 2009, J. Geophys. Res.-Atmos., 121, 3388–3404, https://doi.org/10.1002/2015JD024581, 2016. a
Noguchi, S., Kuroda, Y., Kodera, K., and Watanabe, S.: Robust enhancement of tropical convective activity by the 2019 Antarctic sudden stratospheric warming, Geophys. Res. Lett., 47, e2020GL088743, https://doi.org/10.1029/2020GL088743, 2020. a
Omrani, N.-E., Bader, J., Keenlyside, N. S., and Manzini, E.: Troposphere–stratosphere response to large-scale North Atlantic Ocean variability in an atmosphere/ocean coupled model, Clim. Dynam., 46, 1397–1415, https://doi.org/10.1007/s00382-015-2654-6, 2016. a
O'Neill, A. and Taylor, B. F.: A study of the major stratospheric warming of 1976/77, Q. J. Roy. Meteor. Soc., 105, 71–92, https://doi.org/10.1002/qj.49710544306, 1979. a
Osprey, S. M., Gray, L. J., Hardiman, S. C., Butchart, N., Bushell, A. C., and Hinton, T. J.: The climatology of the middle atmosphere in a vertically extended version of the Met Office's climate model. Part II: Variability, J. Atmos. Sci., 67, 3637–3651, https://doi.org/10.1175/2010JAS3338.1, 2010. a
Osprey, S. M., Butchart, N., Knight, J. R., Scaife, A. A., Hamilton, K., Anstey, J. A., Schenzinger, V., and Zhang, C.: An unexpected disruption of the atmospheric quasi-biennial oscillation, Science, 353, 1424–1427, https://doi.org/10.1126/science.aah4156, 2016. a, b, c, d, e, f, g
O'Sullivan, D.: Interaction of extratropical Rossby waves with westerly quasi-biennial oscillation winds, J. Geophys. Res.-Atmos., 102, 19461–19469, https://doi.org/10.1029/97JD01524, 1997. a, b
Pahlavan, H. A., Fu, Q., Wallace, J. M., and Kiladis, G. N.: Revisiting the quasi-biennial oscillation as seen in ERA5. Part I: description and momentum budget, J. Atmos. Sci., 78, 673–691, https://doi.org/10.1175/JAS-D-20-0248.1, 2021a. a, b
Pahlavan, H. A., Wallace, J. M., Fu, Q., and Kiladis, G. N.: Revisiting the quasi-biennial oscillation as seen in ERA5. Part II: evaluation of waves and wave forcing, J. Atmos. Sci., 78, 693–707, https://doi.org/10.1175/JAS-D-20-0249.1, 2021b. a
Palmer, C. E.: The stratospheric polar vortex in winter, J. Geophys. Res., 64, 749–764, https://doi.org/10.1029/JZ064i007p00749, 1959. a
Palmer, T. N.: Aspects of stratospheric sudden warmings studied from a transformed Eulerian-mean viewpoint, J. Geophys. Res.-Oceans, 86, 9679–9687, https://doi.org/10.1029/JC086iC10p09679, 1981a. a, b
Palmer, T. N.: Diagnostic study of a wavenumber-2 stratospheric sudden warming in a transformed Eulerian-mean formalism, J. Atmos. Sci., 38, 844–855, https://doi.org/10.1175/1520-0469(1981)038<0844:DSOAWS>2.0.CO;2, 1981b. a
Pascoe, C. L., Gray, L. J., Crooks, S. A., Juckes, M. N., and Baldwin, M. P.: The quasi-biennial oscillation: Analysis using ERA-40 data, J. Geophys. Res.-Atmos., 110, D08105, https://doi.org/10.1029/2004JD004941, 2005. a, b, c
Pawson, S., Kodera, K., Hamilton, K., Shepherd, T. G., Beagley, S. R., Boville, B. A., Farrara, J. D., Fairlie, T. D. A., Kitoh, A., Lahoz, W. A., Langematz, U., Manzini, E., Rind, D. H., Scaife, A. A., Shibata, K., Simon, P., Swinbank, R., Takacs, L., Wilson, R. J., Al-Saadi, J. A., Amodei, M., Chiba, M., Coy, L., de Grandpré, J., Eckman, R. S., Fiorino, M., Grose, W. L., Koide, H., Koshyk, J. N., Li, D., Lerner, J., Mahlman, J. D., McFarlane, N. A., Mechoso, C. R., Molod, A., O'Neill, A., Pierce, R. B., Randel, W. J., Rood, R. B., and Wu, F.: The GCM–Reality Intercomparison Project for SPARC (GRIPS): Scientific issues and initial results, B. Am. Meteorol. Soc., 81, 781–796, https://doi.org/10.1175/1520-0477(2000)081<0781:TGIPFS>2.3.CO;2, 2000. a
Peña Ortiz, C., Ribera, P., García-Herrera, R., Giorgetta, M. A., and García, R. R.: Forcing mechanism of the seasonally asymmetric quasi-biennial oscillation secondary circulation in ERA-40 and MAECHAM5, J. Geophys. Res.-Atmos., 113, D16103, https://doi.org/10.1029/2007JD009288, 2008. a
Perlwitz, J. and Graf, H.-F.: The statistical connection between tropospheric and stratospheric circulation of the Northern Hemisphere in winter, J. Climate, 8, 2281–2295, https://doi.org/10.1175/1520-0442(1995)008<2281:TSCBTA>2.0.CO;2, 1995. a
Perlwitz, J. and Harnik, N.: Downward coupling between the stratosphere and troposphere: The relative roles of wave and zonal mean processes, J. Climate, 17, 4902–4909, https://doi.org/10.1175/JCLI-3247.1, 2004. a
Plougonven, R., de la Cámara, A., Hertzog, A., and Lott, F.: How does knowledge of atmospheric gravity waves guide their parameterizations?, Q. J. Roy. Meteor. Soc., 146, 1529–1543, https://doi.org/10.1002/qj.3732, 2020. a
Plumb, R. A.: Instability of the distorted polar night vortex: A theory of stratospheric warmings, J. Atmos. Sci., 38, 2514–2531, https://doi.org/10.1175/1520-0469(1981)038<2514:IOTDPN>2.0.CO;2, 1981. a
Plumb, R. A. and Bell, R. C.: A model of the quasi-biennial oscillation on an equatorial beta-plane, Q. J. Roy. Meteor. Soc., 108, 335–352, https://doi.org/10.1002/qj.49710845604, 1982. a, b
Pohlmann, H., Müller, W. A., Kulkarni, K., Kameswarrao, M., Matei, D., Vamborg, F. S. E., Kadow, C., Illing, S., and Marotzke, J.: Improved forecast skill in the tropics in the new MiKlip decadal climate predictions, Geophys. Res. Lett., 40, 5798–5802, https://doi.org/10.1002/2013GL058051, 2013. a
Pohlmann, H., Müller, W. A., Bittner, M., Hettrich, S., Modali, K., Pankatz, K., and Marotzke, J.: Realistic quasi-biennial oscillation variability in historical and decadal hindcast simulations using CMIP6 forcing, Geophys. Res. Lett., 46, 14118–14125, https://doi.org/10.1029/2019GL084878, 2019. a, b
Polavarapu, S., Shepherd, T. G., Rochon, Y., and Ren, S.: Some challenges of middle atmosphere data assimilation, Q. J. Roy. Meteor. Soc., 131, 3513–3527, https://doi.org/10.1256/qj.05.87, 2005. a
Portal, A., Ruggieri, P., Palmeiro, F. M., García-Serrano, J., Domeisen, D. I. V., and Gualdi, S.: Seasonal prediction of the Boreal winter stratosphere, Clim. Dynam., 58, 2109–2130, https://doi.org/10.1007/s00382-021-05787-9, 2022. a, b
Quiroz, R. S.: The association of stratospheric warmings with tropospheric blocking, J. Geophys. Res.-Atmos., 91, 5277–5285, https://doi.org/10.1029/JD091iD04p05277, 1986. a
Rajendran, K., Moroz, I. M., Osprey, S. M., and Read, P. L.: Descent rate models of the synchronization of the quasi-biennial oscillation by the annual cycle in tropical upwelling, J. Atmos. Sci., 75, 2281–2297, https://doi.org/10.1175/JAS-D-17-0267.1, 2018. a
Randel, W. J., Wu, F., Swinbank, R., Nash, J., and O’Neill, A.: Global QBO circulation derived from UKMO stratospheric analyses, J. Atmos. Sci., 56, 457–474, https://doi.org/10.1175/1520-0469(1999)056<0457:GQCDFU>2.0.CO;2, 1999. a
Rao, J., Ren, R., Chen, H., Yu, Y., and Zhou, Y.: The stratospheric sudden warming event in February 2018 and its prediction by a climate system model, J. Geophys. Res.-Atmos., 123, 13332–13345, https://doi.org/10.1029/2018JD028908, 2018. a
Rao, J., Ren, R., Chen, H., Liu, X., Yu, Y., Hu, J., and Zhou, Y.: Predictability of stratospheric sudden warmings in the Beijing Climate Center forecast system with statistical error corrections, J. Geophys. Res.-Atmos., 124, 8385–8400, https://doi.org/10.1029/2019JD030900, 2019. a
Reed, R. J., Campbell, W. J., Rasmussen, L. A., and Rogers, D. G.: Evidence of a downward-propagating, annual wind reversal in the equatorial stratosphere, J. Geophys. Res., 66, 813–818, https://doi.org/10.1029/JZ066i003p00813, 1961. a, b
Reed, R. J., Wolfe, J. L., and Nishimoto, H.: A spectral analysis of the energetics of the stratospheric sudden warming of early 1957, J. Atmos. Sci., 20, 256–275, https://doi.org/10.1175/1520-0469(1963)020<0256:ASAOTE>2.0.CO;2, 1963. a
Richter, J. H., Sassi, F., and Garcia, R. R.: Toward a physically based gravity wave source parameterization in a general circulation model, J. Atmos. Sci., 67, 136–156, https://doi.org/10.1175/2009JAS3112.1, 2010. a
Richter, J. H., Anstey, J. A., Butchart, N., Kawatani, Y., Meehl, G. A., Osprey, S., and Simpson, I. R.: Progress in simulating the quasi-biennial oscillation in CMIP models, J. Geophys. Res.-Atmos., 125, e2019JD032362, https://doi.org/10.1029/2019JD032362, 2020. a, b, c
Richter, J. H., Butchart, N., Kawatani, Y., Bushell, A. C., Holt, L., Serva, F., Anstey, J., Simpson, I. R., Osprey, S., Hamilton, K., Braesicke, P., Cagnazzo, C., Chen, C.-C., Garcia, R. R., Gray, L. J., Kerzenmacher, T., Lott, F., McLandress, C., Naoe, H., Scinocca, J., Stockdale, T. N., Versick, S., Watanabe, S., Yoshida, K., and Yukimoto, S.: Response of the quasi-biennial oscillation to a warming climate in global climate models, Q. J. Roy. Meteor. Soc., 148, 1490–1518, https://doi.org/10.1002/qj.3749, 2022. a, b, c, d
Rind, D., Suozzo, R., and Balachandran, N. K.: The GISS Global Climate-Middle Atmosphere Model. Part II. Model Variability Due to Interactions between Planetary Waves, the Mean Circulation and Gravity Wave Drag, J. Atmos. Sci., 45, 371–386, https://doi.org/10.1175/1520-0469(1988)045<0371:TGGCMA>2.0.CO;2, 1988. a
Roff, G., Thompson, D. W. J., and Hendon, H.: Does increasing model stratospheric resolution improve extended-range forecast skill?, Geophys. Res. Lett., 38, L05809, https://doi.org/10.1029/2010GL046515, 2011. a, b, c
Runde, T., Dameris, M., Garny, H., and Kinnison, D. E.: Classification of stratospheric extreme events according to their downward propagation to the troposphere, Geophys. Res. Lett., 43, 6665–6672, https://doi.org/10.1002/2016GL069569, 2016. a
Rupp, P. and Birner, T.: Tropospheric eddy feedback to different stratospheric conditions in idealised baroclinic life cycles, Weather Clim. Dynam., 2, 111–128, https://doi.org/10.5194/wcd-2-111-2021, 2021. a
Ryan, R. G., Marais, E. A., Balhatchet, C. J., and Eastham, S. D.: Impact of rocket launch and space debris air pollutant emissions on stratospheric ozone and global climate, Earth's Future, 10, e2021EF002612, https://doi.org/10.1029/2021EF002612, 2022. a
Scaife, A. A., Butchart, N., Warner, C. D., Stainforth, D., Norton, W., and Austin, J.: Realistic quasi-biennial oscillations in a simulation of the global climate, Geophys. Res. Lett., 27, 3481–3484, https://doi.org/10.1029/2000GL011625, 2000. a
Scaife, A. A., Butchart, N., Warner, C. D., and Swinbank, R.: Impact of a spectral gravity wave parametrization on the stratosphere in the Met Office Unified Model, J. Atmos. Sci., 59, 1473–1489, https://doi.org/10.1175/1520-0469(2002)059<1473:IOASGW>2.0.CO;2, 2002. a, b
Scaife, A. A., Athanassiadou, M., Andrews, M., Arribas, A., Baldwin, M., Dunstone, N., Knight, J., MacLachlan, C., Manzini, E., Müller, W. A., Pohlmann, H., Smith, D., Stockdale, T., and Williams, A.: Predictability of the quasi-biennial oscillation and its northern winter teleconnection on seasonal to decadal timescales, Geophys. Res. Lett., 41, 1752–1758, https://doi.org/10.1002/2013GL059160, 2014. a
Scaife, A. A., Karpechko, A. Y., Baldwin, M. P., Brookshaw, A., Butler, A. H., Eade, R., Gordon, M., MacLachlan, C., Martin, N., Dunstone, N., and Smith, D.: Seasonal winter forecasts and the stratosphere, Atmos. Sci. Lett., 17, 51–56, https://doi.org/10.1002/asl.598, 2016. a, b, c, d, e
Scaife, A. A., Baldwin, M. P., Butler, A. H., Charlton-Perez, A. J., Domeisen, D. I. V., Garfinkel, C. I., Hardiman, S. C., Haynes, P., Karpechko, A. Y., Lim, E.-P., Noguchi, S., Perlwitz, J., Polvani, L., Richter, J. H., Scinocca, J., Sigmond, M., Shepherd, T. G., Son, S.-W., and Thompson, D. W. J.: Long-range prediction and the stratosphere, Atmos. Chem. Phys., 22, 2601–2623, https://doi.org/10.5194/acp-22-2601-2022, 2022. a, b
Schenzinger, V., Osprey, S., Gray, L., and Butchart, N.: Defining metrics of the Quasi-Biennial Oscillation in global climate models, Geosci. Model Dev., 10, 2157–2168, https://doi.org/10.5194/gmd-10-2157-2017, 2017. a
Scherhag, R.: Die explosionsartigen Stratosphärenerwärmungen des Spätwinters 1951/52, Berichte des Deutschen Wetterdienstes in der US-Zone, 6, 51–63, 1952. a, b, c, d, e
Scherhag, R.: Stratospheric temperature changes and the associated changes in pressure distribution, J. Atmos. Sci., 17, 575–583, https://doi.org/10.1175/1520-0469(1960)017<0575:STCATA>2.0.CO;2, 1960. a
Schirber, S.: Influence of ENSO on the QBO: Results from an ensemble of idealized simulations, J. Geophys. Res.-Atmos., 120, 1109–1122, https://doi.org/10.1002/2014JD022460, 2015. a
Scott, R. K.: A new class of vacillations of the stratospheric polar vortex, Q. J. Roy. Meteor. Soc., 142, 1948–1957, https://doi.org/10.1002/qj.2788, 2016. a
Scott, R. K. and Haynes, P. H.: Internal interannual variability of the extratropical stratospheric circulation: The low-latitude flywheel, Q. J. Roy. Meteor. Soc., 124, 2149–2173, https://doi.org/10.1002/qj.49712455016, 1998. a
Serva, F., Cagnazzo, C., Christiansen, B., and Yang, S.: The influence of ENSO events on the stratospheric QBO in a multi-model ensemble, Clim. Dynam., 54, 2561–2575, https://doi.org/10.1007/s00382-020-05131-7, 2020. a
Seviour, W. J. M., Hardiman, S. C., Gray, L. J., Butchart, N., MacLachlan, C., and Scaife, A. A.: Skillful seasonal prediction of the Southern Annular Mode and Antarctic ozone, J. Climate, 27, 7462–7474, https://doi.org/10.1175/JCLI-D-14-00264.1, 2014. a, b, c
Seviour, W. J. M., Gray, L. J., and Mitchell, D. M.: Stratospheric polar vortex splits and displacements in the high-top CMIP5 climate models, J. Geophys. Res.-Atmos., 121, 1400–1413, https://doi.org/10.1002/2015JD024178, 2016. a
Sheshadri, A., Plumb, R. A., Lindgren, E. A., and Domeisen, D. I. V.: The vertical structure of annular modes, J. Atmos. Sci., 75, 3507–3519, https://doi.org/10.1175/JAS-D-17-0399.1, 2018. a
Shine, K. P.: The middle atmosphere in the absence of dynamical heat fluxes, Q. J. Roy. Meteor. Soc., 113, 603–633, https://doi.org/10.1002/qj.49711347610, 1987. a, b, c, d
Shiotani, M., Shimoda, N., and Hirota, I.: Interannual variability of the stratospheric circulation in the Southern Hemisphere, Q. J. Roy. Meteor. Soc., 119, 531–546, https://doi.org/10.1002/qj.49711951110, 1993. a
Shuckburgh, E., Norton, W., Iwi, A., and Haynes, P.: Influence of the quasi-biennial oscillation on isentropic transport and mixing in the tropics and subtropics, J. Geophys. Res.-Atmos., 106, 14327–14337, https://doi.org/10.1029/2000JD900664, 2001. a
Sigmond, M., Scinocca, J. F., Kharin, V. V., and Shepherd, T. G.: Enhanced seasonal forecast skill following stratospheric sudden warmings, Nat. Geosci., 6, 98–102, https://doi.org/10.1038/ngeo1698, 2013. a
Simmons, A. J. and Strüfing, R.: Numerical forecasts of stratospheric warming events using a model with a hybrid vertical coordinate, Q. J. Roy. Meteor. Soc., 109, 81–111, https://doi.org/10.1002/qj.49710945905, 1983. a
Simpson, I. R., Hitchcock, P., Seager, R., Wu, Y., and Callaghan, P.: The downward influence of uncertainty in the Northern Hemisphere stratospheric polar vortex response to climate change, J. Climate, 31, 6371–6391, https://doi.org/10.1175/JCLI-D-18-0041.1, 2018. a
Smith, W., Bhattarai, U., Bingaman, D. C., Mace, J. L., and Rice, C. V.: Review of possible very high-altitude platforms for stratospheric aerosol injection, Environmental Research Communications, 4, 031002, https://doi.org/10.1088/2515-7620/ac4f5d, 2022. a
Smy, L. A. and Scott, R. K.: The influence of stratospheric potential vorticity on baroclinic instability, Q. J. Roy. Meteor. Soc., 135, 1673–1683, https://doi.org/10.1002/qj.484, 2009. a
Son, S.-W., Lim, Y., Yoo, C., Hendon, H. H., and Kim, J.: Stratospheric control of the Madden–Julian oscillation, J. Climate, 30, 1909–1922, https://doi.org/10.1175/JCLI-D-16-0620.1, 2017. a
Song, K., Son, S.-W., and Charlton-Perez, A.: Deterministic prediction of stratospheric sudden warming events in the Global/Regional Integrated Model system (GRIMs), Clim. Dynam., 55, 1209––1223, https://doi.org/10.1007/s00382-020-05320-4, 2020. a, b
Song, Y. and Robinson, W. A.: Dynamical mechanisms for stratospheric influences on the troposphere, J. Atmos. Sci., 61, 1711–1725, https://doi.org/10.1175/1520-0469(2004)061<1711:DMFSIO>2.0.CO;2, 2004. a, b
Stockdale, T. N., Kim, Y.-H., Anstey, J. A., Palmeiro, F. M., Butchart, N., Scaife, A. A., Andrews, M., Bushell, A. C., Dobrynin, M., Garcia-Serrano, J., Hamilton, K., Kawatani, Y., Lott, F., McLandress, C., Naoe, H., Osprey, S., Pohlmann, H., Scinocca, J., Watanabe, S., Yoshida, K., and Yukimoto, S.: Prediction of the quasi-biennial oscillation with a multi-model ensemble of QBO-resolving models, Q. J. Roy. Meteor. Soc., 148, 1519–1540, https://doi.org/10.1002/qj.3919, 2022. a, b, c, d, e
Stocker, M., Ladstädter, F., and Steiner, A. K.: Observing the climate impact of large wildfires on stratospheric temperature, Nat. Sci. Rep., 11, 22994, https://doi.org/10.1038/s41598-021-02335-7, 2021. a
Sun, L., Robinson, W. A., and Chen, G.: The predictability of stratospheric warming events: more from the troposphere or the stratosphere?, J. Atmos. Sci., 69, 768–783, https://doi.org/10.1175/JAS-D-11-0144.1, 2012. a
Taguchi, M.: Predictability of major stratospheric sudden warmings: analysis results from JMA operational 1-month ensemble predictions from 2001/02 to 2012/13, J. Atmos. Sci., 73, 789–806, https://doi.org/10.1175/JAS-D-15-0201.1, 2016. a
Taguchi, M.: Comparison of subseasonal-to-seasonal model forecasts for major stratospheric sudden warmings, J. Geophys. Res.-Atmos., 123, 10231–10247, https://doi.org/10.1029/2018JD028755, 2018a. a
Taguchi, M.: Seasonal winter forecasts of the northern stratosphere and troposphere: Results from JMA seasonal hindcast experiments, J. Atmos. Sci., 75, 827–840, https://doi.org/10.1175/JAS-D-17-0276.1, 2018b. a
Taguchi, M. and Hartmann, D. L.: Increased occurrence of stratospheric sudden warmings during El Niño as simulated by WACCM, J. Climate, 19, 324–332, https://doi.org/10.1175/JCLI3655.1, 2006. a
Takahashi, M.: Simulation of the stratospheric quasi-biennial oscillation using a general circulation model, Geophys. Res. Lett., 23, 661–664, https://doi.org/10.1029/95GL03413, 1996. a
Taylor, K. E., Stouffer, R. J., and Meehl, G. A.: An Overview of CMIP5 and the experiment design, B. Am. Meteorol. Soc., 93, 485–498, https://doi.org/10.1175/BAMS-D-11-00094.1, 2012. a
Teisserenc de Bort, L.: Variations de la tempèrature de l’air libre, dans la zone comprise entre 8 et 15 kilomètres d’altitude, C. R. Acad. Sci., 134, 987–989, 1902. a, b
Teweles, S.: Anomalous warming of the stratosphere over North America in early 1957, Mon. Weather Rev., 86, 377–396, https://doi.org/10.1175/1520-0493(1958)086<0377:AWOTSO>2.0.CO;2, 1958. a
Teweles, S. and Finger, F. G.: An abrupt change in stratospheric circulation beginning in mid-January 1958, Mon. Weather Rev., 86, 23–28, https://doi.org/10.1175/1520-0493(1958)086<0023:AACISC>2.0.CO;2, 1958. a
Thompson, D. W. J. and Solomon, S.: Interpretation of recent Southern Hemisphere climate change, Science, 296, 895–899, https://doi.org/10.1126/science.1069270, 2002. a
Thompson, D. W. J. and Wallace, J. M.: The Arctic oscillation signature in the wintertime geopotential height and temperature fields, Geophys. Res. Lett., 25, 1297–1300, https://doi.org/10.1029/98GL00950, 1998. a
Thompson, D. W. J. and Wallace, J. M.: Annular modes in the extratropical circulation. Part I: month-to-month variability, J. Climate, 13, 1000–1016, https://doi.org/10.1175/1520-0442(2000)013<1000:AMITEC>2.0.CO;2, 2000. a, b
Thompson, D. W. J., Baldwin, M. P., and Solomon, S.: Stratosphere-troposphere coupling in the Southern Hemisphere, J. Atmos. Sci., 62, 708–715, https://doi.org/10.1175/JAS-3321.1, 2005. a, b, c
Tian, W., Chipperfield, M. P., Gray, L. J., and Zawodny, J. M.: Quasi-biennial oscillation and tracer distributions in a coupled chemistry-climate model, J. Geophys. Res.-Atmos., 111, D20301, https://doi.org/10.1029/2005JD006871, 2006. a
Tilmes, S., Richter, J. H., Mills, M. J., Kravitz, B., MacMartin, D. G., Garcia, R. R., Kinnison, D. E., Lamarque, J.-F., Tribbia, J., and Vitt, F.: Effects of different dtratospheric SO2 injection altitudes on stratospheric chemistry and dynamics, J. Geophys. Res.-Atmos., 123, 4654–4673, https://doi.org/10.1002/2017JD028146, 2018. a
Tripathi, O. P., Baldwin, M., Charlton-Perez, A., Charron, M., Eckermann, S. D., Gerber, E., Harrison, R. G., Jackson, D. R., Kim, B.-M., Kuroda, Y., Lang, A., Mahmood, S., Mizuta, R., Roff, G., Sigmond, M., and Son, S.-W.: The predictability of the extratropical stratosphere on monthly time-scales and its impact on the skill of tropospheric forecasts, Q. J. Roy. Meteor. Soc., 141, 987–1003, https://doi.org/10.1002/qj.2432, 2015. a, b
Tripathi, O. P., Baldwin, M., Charlton-Perez, A., Charron, M., Cheung, J. C. H., Eckermann, S. D., Gerber, E., Jackson, D. R., Kuroda, Y., Lang, A., McLay, J., Mizuta, R., Reynolds, C., Roff, G., Sigmond, M., Son, S.-W., and Stockdale, T.: Examining the predictability of the stratospheric sudden warming of January 2013 using multiple NWP systems, Mon. Weather Rev., 144, 1935–1960, https://doi.org/10.1175/MWR-D-15-0010.1, 2016. a
Tuck, A. F.: Perspective on aircraft in the stratosphere: 50 years from COMESA through the ozone hole to climate, Q. J. Roy. Meteor. Soc., 147, 713–727, https://doi.org/10.1002/qj.3958, 2021. a
Tung, K. K. and Lindzen, R. S.: A theory of stationary long waves. Part II: Resonant Rossby waves in the presence of realistic vertical shears, Mon. Weather Rev., 107, 735–750, https://doi.org/10.1175/1520-0493(1979)107<0735:ATOSLW>2.0.CO;2, 1979. a
Uryu, M.: On the transport of energy and momentum in stationary waves in a rotating stratified fluid, J. Meteorol. Soc. Jpn., 51, 86–92, https://doi.org/10.2151/jmsj1965.51.2_86, 1973. a
Uryu, M.: Mean zonal flows induced by a vertically propagating Rossby wave packet, J. Meteorol. Soc. Jpn., 52, 481–490, https://doi.org/10.2151/jmsj1965.52.6_481, 1974. a
Vincent, R. A. and Alexander, M. J.: Balloon-borne observations of short vertical wavelength gravity waves and interaction with QBO winds, J. Geophys. Res.-Atmos., 125, e2020JD032779, https://doi.org/10.1029/2020JD032779, 2020. a
Wang, F., Han, Y., Zhang, S., and Zhang, R.: Influence of stratospheric sudden warming on the tropical intraseasonal convection, Environ. Res. Lett., 15, 084027, https://doi.org/10.1088/1748-9326/ab98b5, 2020a. a
Wang, L., Hardiman, S. C., Bett, P. E., Comer, R. E., Kent, C., and Scaife, A. A.: What chance of a sudden stratospheric warming in the Southern Hemisphere?, Environ. Res. Lett., 15, 104038, https://doi.org/10.1088/1748-9326/aba8c1, 2020b. a
Wang, S., Tippett, M. K., Sobel, A. H., Martin, Z. K., and Vitart, F.: Impact of the QBO on prediction and predictability of the MJO convection, J. Geophys. Res.-Atmos., 124, 11766–11782, https://doi.org/10.1029/2019JD030575, 2019. a
Watanabe, S., Hamilton, K., Osprey, S., Kawatani, Y., and Nishimoto, E.: First successful hindcasts of the 2016 disruption of the stratospheric quasi-biennial oscillation, Geophys. Res. Lett., 45, 1602–1610, https://doi.org/10.1002/2017GL076406, 2018. a
Waugh, D. N. W.: Elliptical diagnostics of stratospheric polar vortices, Q. J. Roy. Meteor. Soc., 123, 1725–1748, https://doi.org/10.1002/qj.49712354213, 1997. a, b
Waugh, D. W., Sisson, J. M., and Karoly, D. J.: Predictive skill of an NWP system in the southern lower stratosphere, Q. J. Roy. Meteor. Soc., 124, 2181–2200, https://doi.org/10.1002/qj.49712455102, 1998. a
Woo, S.-H., Sung, M.-K., Son, S.-W., and Kug, J.-S.: Connection between weak stratospheric vortex events and the Pacific decadal oscillation, Clim. Dynam., 45, 3481–3492, https://doi.org/10.1007/s00382-015-2551-z, 2015. a
Yamazaki, K., Nakamura, T., Ukita, J., and Hoshi, K.: A tropospheric pathway of the stratospheric quasi-biennial oscillation (QBO) impact on the boreal winter polar vortex, Atmos. Chem. Phys., 20, 5111–5127, https://doi.org/10.5194/acp-20-5111-2020, 2020. a
Yoo, C. and Son, S.-W.: Modulation of the boreal wintertime Madden-Julian oscillation by the stratospheric quasi-biennial oscillation, Geophys. Res. Lett., 43, 1392–1398, https://doi.org/10.1002/2016GL067762, 2016. a, b, c
Yoshida, K. and Mizuta, R.: Do sudden stratospheric warmings boost convective activity in the Tropics?, Geophys. Res. Lett., 48, e2021GL093688, https://doi.org/10.1029/2021GL093688, 2021. a, b
Yulaeva, E., Holton, J. R., and Wallace, J. M.: On the cause of the annual cycle in tropical lower-stratospheric temperatures, J. Atmos. Sci., 51, 169–174, https://doi.org/10.1175/1520-0469(1994)051<0169:OTCOTA>2.0.CO;2, 1994. a
Zhang, C.: Madden-Julian oscillation, Rev. Geophys., 43, RG2003, https://doi.org/10.1029/2004RG000158, 2005. a
Zhang, J., Xie, F., Ma, Z., Zhang, C., Xu, M., Wang, T., and Zhang, R.: Seasonal evolution of the quasi-biennial oscillation impact on the Northern Hemisphere polar vortex in winter, J. Geophys. Res.-Atmos., 124, 12568–12586, https://doi.org/10.1029/2019JD030966, 2019. a
Zhang, J., Zhang, C., Zhang, K., Xu, M., Duan, J., Chipperfield, M. P., Feng, W., Zhao, S., and Xie, F.: The role of chemical processes in the quasi-biennial oscillation (QBO) signal in stratospheric ozone, Atmos. Environ., 244, 117906, https://doi.org/10.1016/j.atmosenv.2020.117906, 2021. a
Zhang, P., Wu, Y., Simpson, I. R., Smith, K. L., Zhang, X., De, B., and Callaghan, P.: A stratospheric pathway linking a colder Siberia to Barents-Kara Sea sea ice loss, Sci. Adv., 4, eaat6025, https://doi.org/10.1126/sciadv.aat6025, 2018. a
Earlier stratosphere had been used as a geological term for part of the Earth's crust, though that use is now obsolete.
Throughout this review, eastward and westward will be used when referring to wind direction rather than westerly and easterly, respectively, as traditionally chosen by practical meteorologists.
Vertically propagating gravity waves in the extratropics typically have wave lengths that are too small to be resolved by the reanalysis used for Fig. 4 or, indeed, nearly all current climate models, and, therefore, their effect on the mean flow is included in the term in Eq. (3) and not ∇⋅F.
Even though there are no rapid falls in zonal mean temperatures, locally rapid temperature rises can be followed by rapid cooling (e.g. Scherhag, 1952) if, for instance, the polar vortex is displaced from and then back toward the pole.
In mid-September 2019 a significant weakening of the SH polar vortex occurred, but as no actual wind reversal was observed poleward of 60∘, this event was not classified as a major SSW.
In the 1960s the computing community was already using the term “supercomputer”, but it only came into common usage in atmospheric science with the introduction of vector machines capable of around 100 MFLOPS.
- Abstract
- Copyright statement
- Introduction
- Extratropical stratosphere
- Tropical stratosphere
- Tropical–extratropical coupling
- Models and predictability
- Influence on the troposphere
- Outstanding issues
- Data availability
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References
- Abstract
- Copyright statement
- Introduction
- Extratropical stratosphere
- Tropical stratosphere
- Tropical–extratropical coupling
- Models and predictability
- Influence on the troposphere
- Outstanding issues
- Data availability
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References





