Systematic evaluation of the predictability of different Mediterranean cyclone categories

Cyclones are essential components of weather patterns in the densely populated Mediterranean region, providing necessary rainfall for both the environment and human activities. The most intense of them also lead to natural disasters because of their strong winds and heavy precipitation. Identifying sources of errors in the predictability of Mediterranean cyclones is therefore essential to better anticipate and prevent their impact. The aim of this work is to characterise the medium-range cyclone predictability in the Mediterranean. Here, it is investigated in a systematic framework using the European Centre for Medium-Range Weather Forecasts fifth-generation reanalysis (ERA5) and ensemble reforecasts in a homogeneous configuration over the 2001–2021 period. First, a reference dataset of 1960 cyclones is obtained for the period by applying a tracking algorithm to the ERA5 reanalysis. Then the predictability is systematically evaluated in the ensemble reforecasts. It is quantified using a new probabilistic score based on the error distribution of cyclone location and intensity (mean sea level pressure). The score is firstly computed for the complete dataset and then for different categories of cyclones based on their intensity, deepening rate, motion speed, and geographic area and season in which they occur. When crossing the location and intensity errors with the different categories, the conditions leading to poorer or better predictability are discriminated. The motion speed of cyclones appears to be crucial for the predictability of the location: the slower the cyclone, the better the forecast location. In particular, the location of stationary lows located in the Gulf of Genoa is remarkably well predicted. The intensity of deep and rapid-intensification cyclones, occurring mostly during winter, is for its part particularly poorly predicted. This study provides the first systematic evaluation of cyclone predictability in the Mediterranean and opens up possibilities to identify the key processes leading to forecast errors in the region.

1 Introduction

Extratropical cyclones are fundamental components of weather patterns in the mid-latitudes. The frontal systems associated with them provide the majority of the necessary rainfall (Hawcroft et al., 2012), but they can also evolve into damaging storms (e.g. Roberts et al., 2014). A good representation of extratropical cyclones in numerical weather prediction systems is therefore essential to prevent their negative impacts, and identifying sources of forecast error is an important step in understanding the processes leading to poor predictability and improving forecasts.

In the Mediterranean, extratropical cyclones are generally smaller and have a shorter lifetime than in other larger basins (Campins et al., 2011). However, they are at the origin of most of the high-impact weather events in the area, including intense rainfall (e.g. Flaounas et al., 2018), windstorms (e.g. Lfarh et al., 2023), and compound events (e.g. Raveh‐Rubin and Wernli, 2016). The location of the Mediterranean between the tropics and the mid-latitudes, as well as the high mountain chains enclosing the basin, makes it the site of complex interactions. The influence of Alpine lee cyclogenesis (Trigo et al., 2002) and Rossby wave breaking coming from the Atlantic (Raveh-Rubin and Flaounas, 2017) is clearly established in the formation of cyclones in the western part of the basin. Mediterranean cyclogenesis can also be influenced by other mountain ranges, the presence of both polar and subtropical jets, the entrance of Atlantic cyclones into the basin, or heat lows over land (see Flaounas et al., 2022, for a review).

Using a piecewise inversion of the potential vorticity equation, Flaounas et al. (2021) showed that intense Mediterranean cyclones are influenced by two kinds of processes. On the one hand, the intrusion of a potential vorticity streamer into the upper troposphere, related to deviation of the polar jet and to Rossby wave breaking, is identified as a principal dynamical contribution to cyclogenesis. On the other hand, diabatic processes, in particular latent heat release, are important in the lower troposphere, where they act as a source of potential vorticity, reinforcing the cyclonic circulation. The relatively warm Mediterranean Sea can also lead to the formation of tropical-like cyclones, called medicanes, which has received the interest of the scientific community in recent years (e.g. Miglietta et al., 2021). These phenomena can produce severe winds and rainfall, as in the cases of Ianos in September 2020 (Lagouvardos et al., 2022) and Daniel in September 2023. However, medicanes are very rare, with one to two events every year (Cavicchia et al., 2014). Thus, their statistical impact can be considered negligible in our study, which primarily focuses on the predictability of extratropical cyclones in the Mediterranean.

Limitations in the representation of cyclogenesis processes in numerical weather prediction systems can lead to forecast errors propagating through lead times. Additionally and beyond errors associated with the quality of the numerical model, the chaotic nature of the atmosphere leads to an intrinsic limit of predictability (Lorenz, 1969). More precisely, slight differences in the initial conditions can lead to radically different states of the atmosphere as the lead time increases. The forecast error is therefore due to a combination of limitations in the quality of the available observations and to the representation of physical processes in the numerical model, on the one hand, and to the chaotic nature of the atmosphere, on the other hand (practical and intrinsic predictability, respectively; see Melhauser and Zhang, 2012). In the following study, the “practical predictability” will be denoted by “predictability” for simplicity. Earlier work by Zhang et al. (2007) in an idealised baroclinic wave simulation and by Baumgart et al. (2019) in hemisphere-wide simulations of potential vorticity structures identified three phases in forecast error growth. In the first phase, errors in the representation of diabatic processes dominate in the first 12 h of lead time. In the second phase, they are projected to the upper troposphere for between 12 h and 2 d by tropospheric divergence. In the third phase, after a 2 d lead time, the error growth is dominated by the upper-troposphere dynamics.

Ensemble prediction systems have been developed to provide an estimation of the forecast error growth. They offer a measure of forecast uncertainty and different possible scenarios from perturbed initial conditions and model parameterisations (Leutbecher and Palmer, 2008). This is crucial for extreme weather events, which are hardly sampled, especially at longer lead times. By providing a spectrum of the possible outcomes and a measure of the uncertainty, ensemble predictions provide more robust results than a single deterministic forecast. For these reasons, ensemble prediction systems have long proved useful for the early detection of extratropical cyclones and their associated hazards (Buizza and Hollingsworth, 2002) or for assessing the sensitivity of tropical cyclone genesis to the initial conditions (Torn and Cook, 2013). In the Mediterranean, studies based on ensemble forecasts revealed large uncertainty during the formation of medicane case studies. This uncertainty has been traced back to error growth processes occurring along the Rossby wave guide over the North Atlantic a few days ahead (Pantillon et al., 2013; Portmann et al., 2020).

To the best of the authors' knowledge, there is currently no systematic identification of the error sources in the predictability of Mediterranean cyclones. Earlier work highlighted the crucial representation of upper-level dynamical precursors in the western Mediterranean (Argence et al., 2008; Vich et al., 2011) or cloud processes and air–sea interactions for medicanes (Miglietta et al., 2015; Tous et al., 2013), but these results relied on case studies. Using ensemble forecasts, Di Muzio et al. (2019) suggested the existence of a predictability barrier in the formation of several medicanes, but these rare events may not be representative of the broad spectrum of Mediterranean cyclones. Noteworthy, Picornell et al. (2011) assessed the deterministic forecast quality of more than 1000 extratropical cyclones during a whole year and found that the mean error in location increased from 50 km at a 12 h lead time to 118 km at a 48 h lead time. However, the results were limited to relatively short forecast ranges and were not linked with the cyclone characteristics.

On a broader scale, Froude et al. (2007a, b) were among the first to investigate the predictability of extratropical cyclones in a systematic framework. By tracking cyclones in global forecast data across two winter and two summer periods, they quantified errors in both location and intensity, based on comparisons of maximum relative vorticity forecasts with analysis data. For the location, they found out that the error increases almost linearly at a rate of 1.25 geodesic degrees per day. In terms of intensity, they highlighted differences between summer and winter cyclones. In particular, intense storms occurring during the winter period were less accurately predicted, which was attributed to an incorrect representation of their vertical structure. More recent studies followed a similar approach and showed a systematic slow bias in the forecast location of North Atlantic cyclones and a weak underestimation of the intensity for the deepest ones (Pirret et al., 2017; Pantillon et al., 2017). They also explored links between the predictability and the dynamics of cyclogenesis but faced a robustness issue due to limited samples.

In this paper, ensemble reforecasts are used to systematically identify errors in the location and intensity of Mediterranean cyclones. The forecast model covers a 20-year period with the same configuration, which allows for extracting statistically robust signals. The aim of the paper is to characterise cyclone predictability in the Mediterranean region. Their representation in an ensemble prediction system is discussed, and the cyclone characteristics leading to poorer or better predictability are identified. In particular, errors in the prediction of the cyclone location and intensity are evaluated for several categories of cyclones, based on their geographical location and seasonality, intensity, deepening rate, and motion speed.

The article is structured as follows. Section 2 describes the data, cyclone tracking methods, and tools used to evaluate the predictability. The catalogue of Mediterranean cyclones and the associated climatology is presented in Sect. 3. The predictability is evaluated firstly for the whole dataset in Sect. 4 and secondly for specific categories of cyclones in Sect. 5. Finally, Sect. 6 summarises the main results and concludes the study.

2 Data and methods

2.1 Data for the reference tracks: the ERA5 reanalysis

Reanalyses assimilate historical observation data spanning decades with both a fixed assimilation scheme and the same forecast model. ERA5 (Hersbach et al., 2020) is the fifth-generation reanalysis produced by the European Centre for Medium-Range Weather Forecasts (ECMWF). It is based on the Integrated Forecast System (IFS; cycle 41r2) and includes models for the atmosphere, the land surface, and ocean waves. The horizontal resolution of the atmospheric model is about 31 km in the mid-latitudes, and it has 137 vertical levels from the surface to 0.01 hPa. The reanalysis products are available globally with hourly resolution, from 1940 to present. In this study, ERA5 is used from 2001 to 2021 with a 0.25°×0.25° horizontal grid to produce a reference set of cyclone tracks on a domain covering the Mediterranean (25–50° N, 15° W–45° E; see Fig. 1).

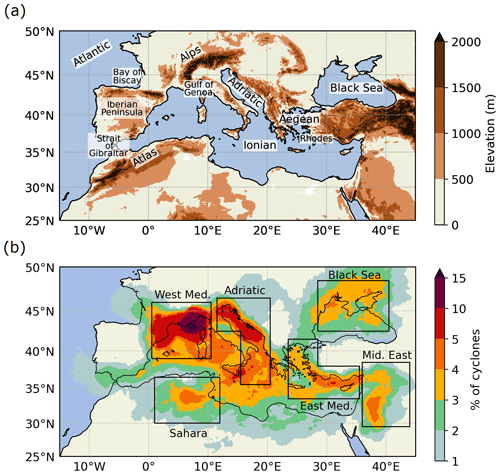
Figure 1 (a) Elevation map over the Mediterranean domain with the toponyms mentioned in the text. (b) Relative frequency of Mediterranean cyclones based on ERA5 over the 2001–2021 period, defined as the percentage of cyclones having a track point within a radius of 100 km. Regions of interest are framed by black boxes. Note that the shading scale is not linear.

2.2 Tracking method for the reference tracks: the AYRAULT algorithm

Before investigating the predictability of Mediterranean cyclones, the first step is to produce a reference catalogue of cyclone tracks. The tracking method is based on the Ayrault (1998) algorithm (later AYRAULT), which has been implemented in the open-source Traject software (Plu and Joly, 2023). Originally designed for Atlantic cyclones in coarse model data (125 km horizontal resolution), AYRAULT had to be adapted for this study. As stated before, Mediterranean cyclones are generally smaller and have shorter lifetimes than those in the Atlantic (Campins et al., 2011), and ERA5 has a higher spatio-temporal resolution than any previous reanalysis used with the algorithm. Therefore, the parameters have been retuned specifically for both ERA5 and the Mediterranean region, starting from the values used in Sanchez-Gomez and Somot (2018).

The main idea of AYRAULT is to track cyclones firstly in the relative vorticity field at 850 hPa. The horizontal wind is then used at both 700 and 850 hPa to choose the best following tracking point in the direction of cyclone propagation. Finally, the track points are paired with the mean sea level pressure (MSLP) field. In the following, a time step is denoted by t; the relative vorticity field at 850 hPa is denoted by ζ; and the zonal and meridional wind fields are denoted by u and v, respectively. AYRAULT can be separated into five steps.

1. Data preparation. A moving average with Gaussian weights is applied to ζ at 850 hPa and to u and v at 850 and 700 hPa to remove noisy features into these fields. The characteristic length in the weight decay is 225 km for ζ (to keep a sufficient number of relevant vorticity cores) and 280 km for the wind fields (to keep the environmental wind and avoid the vortex wind anomaly).

2. Detection of ζ maxima. Local maxima are detected in the ζ-smoothed field. A single maximum (the strongest one) is retained within a radius of 300 km.

3. Loop over successive time steps. For every ζ maximum at time t, a corresponding maximum at time t+1 is searched for using a three-step method. First, the ζ maximum at time t is advected by the wind at both 850 and 700 hPa, giving two guess positions for time t+1. In a second step, a new ζ maximum at time t+1 is searched for in the neighbourhood of the two guessed points, within a radius of 300 km. Third and last, two quality criteria, based on the distance between the guessed point and the new ζ location and on the ζ-value variation, must be fulfilled in order to keep a vortex core at t+1. A cyclone track is finally defined by the successive positions of ζ maxima at every time step.

4. Pairing with MSLP. For every point belonging to the track, the local minimum of MSLP located within a 3° square centred on the ζ maximum becomes the new track point.

5. Validation criteria. The tracking process is stopped if the value of the ζ maximum is less than 10⁻⁴ s⁻¹ or if the MSLP minimum is greater than 1015 hPa. Among all tracks, only those which last for longer than 24 h and reach at least 1005 hPa during their lifetime are retained. This last criterion avoids most of the artefact cyclones. Indeed, some of the cases with the deepest MSLP over 1005 hPa appear to be local secondary lows caused by stronger storms crossing northern Europe. Finally, an additional criterion is applied to only retain tracks entering into either the Mediterranean Sea or the Black Sea.

The Mediterranean-adapted version of AYRAULT previously described has been successfully tested with a slightly different configuration in an intercomparison of 10 tracking methods applied to ERA5 (Flaounas et al., 2023). The produced dataset remained close to the consensus between all algorithms in the spatial and seasonal distributions of cyclones. In the present study, our dataset is used as a reference instead of the consensus produced by Flaounas et al. (2023) for two principal reasons. First, the latter contains only 206 tracks in the highest confidence level (i.e. consensus of the 10 algorithms), which is not enough for a systematic study. At the mean confidence level (i.e. consensus of 5 of 10 algorithms), for the 2001–2021 period and with the same thresholds used here for the pressure and location of cyclones, 1231 tracks are detected in Flaounas et al. (2023), compared to 2853 with AYRAULT. Second, AYRAULT is conceptually similar to the tracking algorithm applied to the reforecasts (see Sect. 2.4), which reduces the influence of the tracking method on the results to focus on the predictability.

2.3 Data for the predicted tracks: the IFS ensemble reforecasts

Reforecasts are forecasts made retrospectively starting from historical initial conditions with a fixed model version. They are a key tool for investigating the predictability of the Mediterranean cyclones previously tracked in ERA5. The ECMWF ensemble reforecasts used here are constituted of 10 perturbed + 1 control members based on the IFS model (cycle 47r3) and initialised from ERA5 (Vitart et al., 2019). Initial perturbations of the reanalysis are constructed from the ERA5 ensemble data assimilation and singular vectors. Additionally, the model uncertainties are represented using a stochastically perturbed parameterisation tendency scheme (Buizza et al., 1999). The reforecasts used here cover a historical period of 20 years from October 2001 to October 2021, during which they are initialised every Monday and Thursday at 00:00 UTC, leading to a total of about 2000 base times. The output spatial resolution of 0.25° is identical to the one in the ERA5 reanalysis. For each base time, a forecast output is available every 6 h (temporal resolution coarser than ERA5). Despite the maximum lead time of 14 d available with a constant resolution in the reforecasts, the maximum lead time is restricted in this study to 144 h (6 d) because of the short lifetime of Mediterranean cyclones, considering that only less than 1 % of the cyclones from our reference dataset last longer than 6 d. The small number of ensemble members able to produce cyclone tracks at longer lead times (see Sect. 4.1) points to the need for a limitation of the maximum lead time. Note that the same cyclone can be tracked in two successive forecast initialisations. When this happens, the two forecasts are treated independently.

2.4 Tracking method for the predicted tracks: the VDG algorithm

In the reforecasts, the tracking of the cyclones is made with another algorithm (van der Grijn, 2002; hereafter VDG), developed at the ECMWF and originally designed for the operational tracking of tropical cyclones. The VDG algorithm, also implemented in the open-source Traject software (Plu and Joly, 2023), is similar to the one previously applied (AYRAULT), as it also uses MSLP, the ζ-smoothed field at 850 hPa, and the horizontal wind at 850 and 700 hPa. The main difference between the two algorithms is that VDG starts the tracking from a given geographical point or from an existing track. This characteristic is particularly useful when it comes to detecting cyclones in the reforecasts from the location of the reference tracks. Cyclones detected in ERA5 are indeed directly linked with the reforecast by the construction of VDG, as the position of the cyclone in the reforecast at the initial time r(0) is directly dependent on the presence of a reference track at the same time. Applying AYRAULT to the reforecasts would have required an additional step for matching the forecast and observed cyclones, bringing more complexity.

At initialisation time, a ζ maximum is searched for in the reforecast field, in the neighbourhood of the reference track (previously calculated in ERA5). The tracking in VDG is then independent of the reference track and is based on a combination of the past-movement and steering-flow vector V_av, defined as the layer average of the local wind fields at 850 and 700 hPa. In the following, r and r_fg are, respectively, the positions of the cyclone and of the first guess. Apart from the initial step, the VDG algorithm can be divided as follows.

1. First guess. The steering-flow V_av and the past-movement $\mathit{r}\left(t\right)-\mathit{r}(t-\mathrm{1})$ vectors are combined to obtain the first-guess position of the next tracking point r_fg using the equation ${\mathit{r}}_{\mathrm{fg}}(t+\mathrm{1})=\mathit{r}\left(t\right)+w\left[\mathit{r}\right(t)-\mathit{r}(t-\mathrm{1}\left)\right]+(\mathrm{1}-w){\mathit{V}}_{\mathrm{av}}\mathit{\delta }t$. w is a weight parameter ranging from 0 to 1 depending on the temporal resolution of the forecast δt and here set to 0.4. NB at the first time step, only the steering-flow vector is used (there is no past movement).

2. Detection of the ζ maximum. A maximum is searched for in the ζ field within a square of 5° centred around the first guess.

3. Pairing with MSLP. Another search is performed for the MSLP minimum within a same square of 5°, centred this time on the ζ maximum. The position of this MSLP point finally becomes the next track point r(t+1).

4. Stopping criteria. The tracking of the cyclone is stopped when the value of the vorticity maximum ζ is less than the corresponding threshold of 10⁻⁴ s⁻¹ or when the value of the MSLP minimum is greater than 1015 hPa, as in AYRAULT. This last criterion also implies that the tracking begins only if a MSLP minimum is found below the pressure threshold. The validation criteria assuring that cyclones last longer than 24 h and reach at least 1005 hPa during their lifetime (applied with AYRAULT) are not applied here in the reforecasts.

2.5 Comparison of tracking algorithms and final reference dataset

As demonstrated by Flaounas et al. (2023), using different cyclone tracking methods often leads to different results in the Mediterranean. In this study, 2853 cyclones are detected with AYRAULT in ERA5 for the 2001–2021 period, while cyclones are detected in the reforecasts using VDG starting from the reference tracks previously built. Using different tracking methods for the reference and the reforecast tracks can introduce biases into the analysis. To assess the robustness of the results, VDG is also applied to the ERA5 data, using the tracks detected by AYRAULT as a reference. Note that VDG is applied to 6 h ERA5 data for consistency with the temporal resolution of the reforecasts for which it is tuned. For each track detected by both algorithms, the difference in terms of location and intensity is calculated for all simultaneous track points. For 85 % of the tracks, no difference is found between the two algorithms. However, for 10 % of the dataset, the distance between AYRAULT and VDG tracks reaches almost 200 km at the time of minimum MSLP. To avoid this discrepancy, tracks are removed from the reference dataset if they are detected in ERA5 by AYRAULT but not by VDG (206 tracks) or if the maximal distance between them reaches more than 40 km (687 tracks). With these two criteria, the two algorithms provide identical tracks in 99 % of the dataset for both location and intensity. The following results are based on the remaining 1960 cyclones tracks that satisfy these two criteria.

2.6 Predictability metrics

The predictability is investigated using the error and spread in both location and intensity. The relationship between the mean error and spread is used to verify the ensemble reliability before proceeding with further quantification of the predictability. For a reliable ensemble, one should expect the mean error and spread to be comparable in magnitude.

In the following, errors are calculated by comparing the location and the intensity of each ensemble member with the corresponding reference track in ERA5, at each time t of the cyclone lifetime. The spread is for its part calculated from the pairwise difference between the members of the ensemble.

To assess the predictability of the cyclone location, we use the total track error (TTE) as defined in Froude et al. (2007b) and Leonardo and Colle (2017). TTE is also decomposed into along-track error (ATE) and cross-track error (CTE). A positive (negative) ATE stands for a forecast track ahead (behind) the reference track, while a positive (negative) CTE stands for a forecast track on the left-hand side (on the right-hand side) of the reference track. Track errors (TTE, ATE, and CTE) are calculated for each member individually and are presented in Sect. 4. Additionally, $\stackrel{\mathrm{‾}}{\mathrm{TTE}}$ is here defined for each forecast cyclone as the mean of the TTEs of the members at each time t of the cyclone lifetime. The spread in location (hereafter σ_loc) is determined by averaging the distance between each pair of members as follows:

$$\begin{array}{}\text{(1)}& {\mathit{\sigma }}_{\mathrm{loc}}\left(t\right)={\displaystyle \frac{\mathrm{1}}{N(N-\mathrm{1})/\mathrm{2}}}\sum _{\mathrm{1}\le i<j\le N}d\left({\mathit{r}}^i\left(t\right),{\mathit{r}}^j\left(t\right)\right),\end{array}$$

where N is the number of members in which the cyclone is detected by the tracking algorithm at time t, rⁱ (r^j) is the position of the cyclone in the ith member (in the jth member), and d is the geodesic distance between the two positions.

Regarding the cyclone intensity, the MSLP error (hereafter MSLPE) is defined for each member as the difference between the MSLP of the member and the MSLP of the reference track at the same time. Unlike errors in the location, MSLPEs can also be negative. Consequently, 〈MSLPE〉 is defined as the root mean square of the MSLPEs over the members, for a specific track and at a specific time t of the cyclone lifetime. The spread in MSLP (hereafter σ_int) is for its part determined from the root mean square of the differences between each pair of members as follows:

$$\begin{array}{}\text{(2)}& {\mathit{\sigma }}_{\mathrm{int}}\left(t\right)=\sqrt{{\displaystyle \frac{\mathrm{1}}{N(N-\mathrm{1})/\mathrm{2}}}\sum _{\mathrm{1}\le i<j\le N}{\left(p^i\left(t\right)-p^j\left(t\right)\right)}^{\mathrm{2}}},\end{array}$$

where pⁱ (p^j) is the MSLPE of the ith member (jth member).

An additional metric is defined to compare distributions of TTE or MSLPE between different categories of cyclones (see Sect. 5). In a preliminary step, for each category of cyclone, a cumulative density function (CDF) of errors is constructed by taking into account every member of every cyclone track found at each lead time τ. CDFs of errors are then compared in a framework close to the continuous ranked probability score (CRPS) described in Candille et al. (2007). The metric denoted here by cumulative density function error (later CDFE) measures the distance between a CDF of errors and a virtual null-error distribution (100 % of the errors equal to 0):

$$\begin{array}{}\text{(3)}& \mathrm{CDFE}\left(F_{\mathit{\tau }}\right)=\int {\left[F_{\mathit{\tau }}\left(x\right)-{\mathrm{1}}_{x\ge \mathrm{0}}\right]}^{\mathrm{2}}\mathrm{d}x,\end{array}$$

here F_τ(x) is the CDF of the errors (either TTEs or MSLPEs) at a specific lead time τ and 1_x≥0 stands for the Heaviside step function. Note that the CDFE metric has the same dimension as the variable on which it is applied. A higher (smaller) CDFE indicates poorer (better) predictability. At each lead time, the statistical significance is evaluated using the Kolmogorov–Smirnov test, which in our case determines if two CDFs of errors are similar or not at a confidence level of 95 %. This will ensure the robustness of the difference in the predictability of several categories of cyclones presented with the CDFE metric.

3 Climatology of the reference dataset

This section provides the climatology of our reference dataset, based on the Mediterranean cyclones tracked with AYRAULT in ERA5 data and satisfying the two criteria of Sect. 2.5. In particular, the spatial distribution, the seasonal cycle, the intensity, and the motion speed of cyclones are presented. Figure 1a shows the ground elevation over the Mediterranean and toponyms that will be used in this paper.

3.1 Spatial distribution

For the whole 2001–2021 period, a total of 1960 cyclones are detected in the Mediterranean region, i.e. about 100 cyclones every year on average. The colour shading in Fig. 1b accounts for the number of tracks having at least one track point within a radius of 100 km, divided by the total number of tracks. The figure can thus be seen as the relative frequency of cyclone occurrence in our reference dataset, regardless of their stage of development. The spatial distribution is not homogeneous, as the majority of cyclones are concentrated in preferred regions. In particular, six regions of interests, designed to cover equal areas, are identified here by visual examination of the spatial distribution.

The six preferred regions account for 63 % of the cyclones in the dataset. The most active of them is the West Mediterranean (22 %). It includes the Gulf of Genoa, in the lee of the Alps, which is recognised as the most cyclogenetic area (Trigo et al., 2002). Following it are the regions of the Adriatic (11 %), the East Mediterranean (10 %), the Black Sea (7 %), the Sahara (7 %), and finally the Middle East (6 %). The importance of the Alps in the formation of the West Mediterranean cyclones is clearly established (Trigo et al., 2002). Horvath et al. (2008) show that lee cyclogenesis is also the dominant formation process for Adriatic cyclones, whether they form in the Gulf of Genoa or in the Adriatic itself. The same orographic processes are known to play a role in the formation of Saharan cyclones in the lee of Atlas Mountains (Winstanley, 1972; Alpert and Ziv, 1989), while Thorncroft and Flocas (1997) and Prezerakos et al. (2006) mostly highlighted the importance of interactions between the polar and the subtropical jets in Saharan cyclogenesis. For the Black Sea and generally in the eastern parts of the Mediterranean, Trigo et al. (2002) argued that cyclones are formed by different processes. In particular, they stated that surface cyclones in the Black Sea seem to be associated with an upper trough in the west of the region, advecting vorticity toward a relatively warm sea. Similar processes are found in the Aegean. The same authors argued that cyclones in the Middle East are the manifestation of extensions of the Asian trough in late spring.

The overall spatial distribution of our dataset is in agreement with previous studies (Alpert et al., 1990; Trigo et al., 1999; Maheras et al., 2001; Campins et al., 2011; Lionello et al., 2016; Aragão and Porcù, 2022; Flaounas et al., 2023). However, two minor differences remain. First, the hotspot in the western Atlas Mountains and the high density of cyclones over the Iberian Peninsula described in the literature do not appear here. This is mainly due to the criteria used to construct our dataset by removing weak thermal lows with a pressure threshold of 1005 hPa, on the one hand, and by removing cyclones that do not enter into either the Mediterranean Sea or the Black Sea, on the other hand. Second, the high density of cyclones found here in the Adriatic is not highlighted in the majority of previous studies.

3.2 Seasonal cycle

Figure 2 shows the number of cyclones striking any of the six regions of interest during each month of the year, averaged over the 20 years of our dataset. One can see that the number of cyclones in the Mediterranean is highly dependent on the season. The peak activity spans from November to May, while the period from June to October experiences fewer occurrences. However, this general trend is also dependent on the region considered.

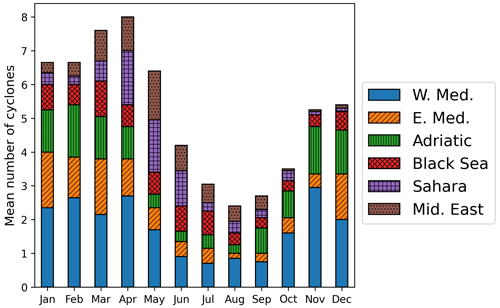
Figure 2 Monthly number of cyclones in the six regions defined in Fig. 1b. Cyclones are counted at their minimum MSLP point and averaged over the 20-year period.

In the West Mediterranean and in the Adriatic, the cold season generally experiences more cyclones. Horvath et al. (2008) came to the same conclusion for the majority of Adriatic cyclones while highlighting the importance of a subcategory of summer cyclones for their association with high-impact weather. In the East Mediterranean, more cyclones are also found during the cold part of the year. Saharan cyclones clearly exhibit a peak of occurrence in April and May, in agreement with previous studies (Winstanley, 1972; Alpert et al., 1990; Trigo et al., 2002). The Black Sea has a unique seasonal cycle, with a few occurrences from August to November and a higher level of activity during a long period spanning from December to July. The presence of those cyclones during a large part of the year was already observed in Trigo et al. (1999). For the case of Middle East cyclones, a higher level of occurrences is found here from March to May, while Trigo et al. (2002) found the peak of activity in August.

3.3 Intensity and deepening rate

Figure 3a shows the spatial distribution of the 10 % deepest cyclones in the reference dataset. They are mainly concentrated in the West Mediterranean and in the Adriatic, while some deep cyclones are found in the north-western parts of the Black Sea. The West Mediterranean and the Adriatic are also two hotspots of rapid intensification when looking at the deepening rates (not shown). While cyclones in these two areas are influenced by the Atlantic (Raveh-Rubin and Flaounas, 2017), the origin of deep cyclones in the north-western Black Sea remains unclear. Noteworthy, cyclones in this region do not experience rapid intensification. In contrast, the shallowest cyclones are concentrated in the Gulf of Genoa, highlighting the broad spectrum of intensities in the West Mediterranean. The other shallow cyclones are found mainly in the East Mediterranean and in the eastern parts of the Black Sea (not shown).

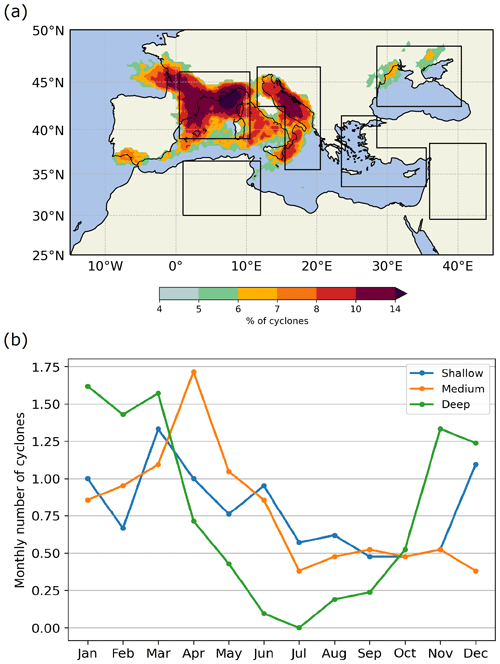
Figure 3 (a) Relative frequency of Mediterranean cyclones, defined as the percentage of the 10 % deepest cyclones having a track point within a radius of 100 km. Note that the shading scale is not linear. (b) Monthly mean number of cyclones in the three categories of intensity. Each category contains 10 % of the dataset, i.e. the 10 % deepest cyclones (green curve), the 10 % of cyclones around the median intensity (orange curve), and the 10 % shallowest cyclones (blue curve).

Figure 3b presents the typical seasonal cycle for three intensity-based categories of Mediterranean cyclones. Shallow and medium-intensity cases are more present during spring and exhibit a flat minimum from July to November. The 10 % deepest cyclones (green curve) show a more pronounced seasonal cycle, with very few cyclones during the warm part of the year and a peak of activity from November to March. The similar pattern is observed for rapid-intensification cyclones, which are found almost exclusively during the cold part of the year (not shown).

3.4 Motion speed

The motion speed of a cyclone is defined here by the median speed along its whole lifetime. According to our calculations for the reference dataset, Mediterranean cyclones move on average eastward at a median motion speed of 25 km h⁻¹. However the variability is large, and the fastest 5 % move at speeds greater than twice the median. Figure 4 shows the spatial distribution of the cyclones in each of the three motion speed categories: the 10 % fastest cyclones (Fig. 4a), the 10 % of cyclones around the median speed (Fig. 4b), and the 10 % slowest cyclones (Fig. 4c). The strong changes in spatial patterns between the different motion-speed-based categories highlight the close relationship between the region in which the Mediterranean cyclone evolves and its motion speed.

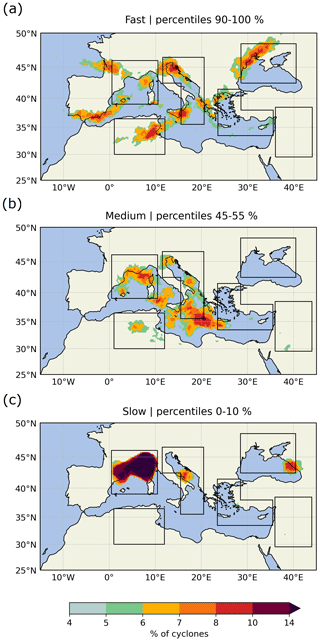
Figure 4 Relative frequency of occurrences (as defined in Fig. 3a) for the three motion-speed-based categories. Each category contains 10 % of the dataset, i.e. (a) the 10 % fastest cyclones, (b) the 10 % of cyclones around the median speed, and (c) the 10 % slowest cyclones. The black boxes are the regions of interests defined in Fig. 1b. Note that the shading scale is not linear.

The fastest cyclones (Fig. 4a) can be found in several particular areas. First, cyclones originating from the Sahara are clearly marked along an axis from the south of the Atlas Mountains to the Ionian Sea. Cyclones in this region are also the fastest, with a median speed of 30 km h⁻¹. This result is in agreement with previous studies, which often highlight the high velocities of Saharan cyclones compared to other Mediterranean lows (Alpert and Ziv, 1989; Kouroutzoglou et al., 2011). Second, fast Atlantic cyclones enter into the West Mediterranean, mainly from the Bay of Biscay or through the Strait of Gibraltar. Third, another group of fast cyclones crosses the western Black Sea. Fourth and last, two other favourable regions for fast cyclones are found in the northern Adriatic and in western Greece. Medium-speed cyclones (Fig. 4b) are for their part mainly located over sea, in the West Mediterranean, in the Adriatic, and in the Ionian Sea. Finally, the slowest cyclones (Fig. 4c) are clearly concentrated in the West Mediterranean, with a median motion speed of around 17 km h⁻¹. Some quasi-stationary lows can also be found in the eastern parts of the Black Sea. The location of these last quasi-stationary lows contrasts with the fast cyclones observed over the western Black Sea (Fig. 4a), suggesting two different types of cyclones in the Black Sea area.

4 Evaluation of the ensemble reforecasts

This section is dedicated to the evaluation of the representation of Mediterranean cyclones in the reforecasts. Errors in location and intensity, as defined in Sect. 2, are firstly evaluated by taking the tracks detected in ERA5 as a reference, while the reliability of the ensemble reforecasts is assessed in a second step.

4.1 Location and intensity errors

To evaluate the reforecasts, both errors in location and intensity are considered. In Fig. 5, distributions of errors are computed at each lead time by taking into account the individual error of each member of the ensemble for the entire dataset. The large number of 1960 cyclone tracks ensures that the results are robust. The mean number of members in which a cyclone is found by VDG decreases approximately linearly as the lead time increases (orange curve in Fig. 5). While more than 9 members out of 11 detect a cyclone at the initial time, less than 4 members remain on average after a 144 h lead time.

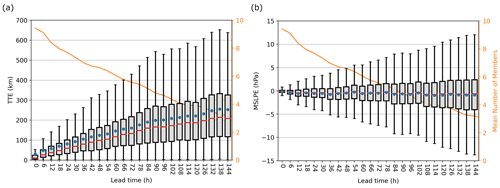
Figure 5 Distributions of (a) total track errors (TTEs) and (b) MSLP errors (MSLPEs) relative to ERA5 as a function of lead time. Means are depicted by the blue circles, medians are depicted by the red lines, the first to third quartiles are depicted by grey boxes, and the minima and maxima are depicted by black whiskers. The orange curve is the mean number of members in which a cyclone is detected.

The distribution of TTEs is presented for each lead time up to 144 h (Fig. 5a). Both the median error and interquartile range increase as the lead time increases. For instance, after a 72 h lead time, 50 % of the TTEs span from 80 to 220 km. Interestingly, the error growth is slower than linear and seems to exhibit two phases: during the first 78 h, the median TTE increases by about 40 km d⁻¹, while it increases at a smaller rate of about 20 km d⁻¹ from a 84 h lead time onward. This behaviour can be explained by two different factors. Firstly, the construction of VDG constrains the tracking to start near the reference track. Given that the median lifetime of the cyclones of our dataset is 42 h, as the lead time increases, the proportion of cyclones tracked from early lead times (where the forecast track may have diverged from the reference track) decreases, compared to those tracked from longer lead times (where the forecast track remains close to the reference track). As a result, the error growth tends to slow down as the lead time increases. Second, the phenomenon of error saturation also plays a role. For long enough lead times, an ensemble forecast is expected to converge toward the climatological distribution. Consequently, the mean and median errors are anticipated to increase at a slower rate at long lead times and ultimately saturate at constant values.

Overall, the growth rate of 40 km d⁻¹ in the first 78 h lead time is remarkably close to the 43 km d⁻¹ found by Picornell et al. (2011) in the Mediterranean. The authors used for their part the ECMWF operational deterministic model during the 2006–2007 period and evaluated errors only during the first 48 h, which may explain the comparable error growth despite the older model version used in their study. In the extratropical Northern Hemisphere and using the operational ensemble prediction system of the ECMWF from January to July 2005, Froude et al. (2007b) found a much higher mean error growth rate of 1.25° (about 137 km) every day, almost constant until a 7 d lead time. The coarser resolution of the ensemble prediction system used in their study (about 80 km) and the particular characteristics of Mediterranean cyclones could explain this difference in the mean error growth rate.

As presented in Sect. 2.6, TTE can be decomposed into ATE and CTE. ATE exhibits a weak and constant bias of −15 km at a 72 h lead time and beyond, indicating that forecast tracks propagate more slowly on average compared to the reference (not shown). It is in agreement with Froude et al. (2007a), who highlighted that forecast cyclones in the IFS model are on average too slow by about 1 km h⁻¹ compared to the analysis. Pirret et al. (2017) and Pantillon et al. (2017) also found a systematic slow bias in the prediction of 60 and 25 severe European storms, respectively. The little bias found here in ATE, however, is much smaller than in the previously mentioned studies. Regarding CTE, a weak positive systematic shift is observed, growing at a constant rate of 4 km d⁻¹, indicating a weak shift to the left of the track (not shown). When looking into absolute values of ATE and CTE, it appears that TTE is the result of an equivalent contribution of both components.

Errors in intensity (MSLPE) are presented in Fig. 5b. The bias quickly reaches −0.5 hPa in the first 12 h lead time, and forecasts continue to deviate at a very slow rate of −0.1 hPa d⁻¹ until 144 h. This argues in favour of a well-centred error distribution of the ensemble reforecasts with a slight overestimation of the cyclone intensity, as in Froude et al. (2007b). After 72 h of forecast, 50 % of the MSLPEs are between −2.5 and 1.5 hPa and the interquartile range grows linearly to 0.9 hPa until the last lead time. When looking at the absolute MSLPE (not shown), a little linear bias of 0.6 hPa d⁻¹ is observed. Froude et al. (2007b) highlighted an even smaller bias of around 0.2 hPa d⁻¹ for the extratropical Northern Hemisphere. It could indicate a better prediction of the intensity of cyclones in other basins compared to the Mediterranean; however, the small magnitude of these biases should be considered.

4.2 Reliability of the ensemble reforecasts

The reliability of the ensemble reforecasts is evaluated for both the intensity and location by comparing the spread and the mean error of the ensemble for each cyclone and at a specific lead time, as defined in Sect. 2.6. One expects the mean error to be close to the spread for a reliable ensemble, while a mean error greater (smaller) than the spread indicates an under-dispersive (over-dispersive) ensemble prediction system.

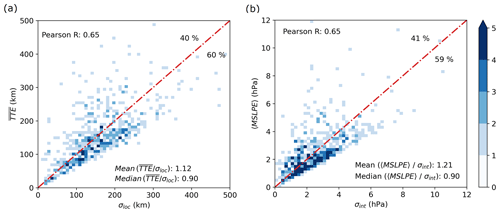
Figure 6 Spread–skill relationship at a 72 h lead time. The blue shading represents the number of cyclones populating each bin. (a) Mean of the TTEs of the members, denoted by $\stackrel{\mathrm{‾}}{\mathrm{TTE}}$, compared to the spread in location, denoted by σ_loc. The bin length is equal to 8 km. (b) Root mean square of the MSLPEs of the members, denoted by 〈MSLPE〉, compared to the spread in intensity, denoted by σ_int. The bin length is equal to 0.2 hPa. The red curve represents an idealised, perfectly reliable set of ensemble reforecasts with a mean error equivalent to the spread. Percentages indicate the proportion of cyclones above and below the diagonal, respectively.

Figure 6 presents a comparison between the spread and the mean error of the ensemble at a 72 h lead time for the location (Fig. 6a) and for the intensity (Fig. 6b). Similar observations can be made for both aspects: firstly, the ensemble is reasonably reliable, with an identifiable linear relationship between the spread and mean error (correlation coefficient equal to 0.65). Secondly, there is a slight but noticeable over-dispersion, with about 60 % of cyclone forecasts presenting a spread greater than the mean error. Finally, the ratio of mean error to the spread is equal to 1.12 for the location and 1.21 for the intensity, while the median ratio is equal to 0.90 in both cases. This indicates that while the ensemble tends to be over-dispersive in most forecasts, some of them are totally off, with a mean error much greater than the spread. It is noticeable that the opposite case with a spread much greater than the mean error is not really observed. Note that these three conclusions remain valid for all lead times (not shown).

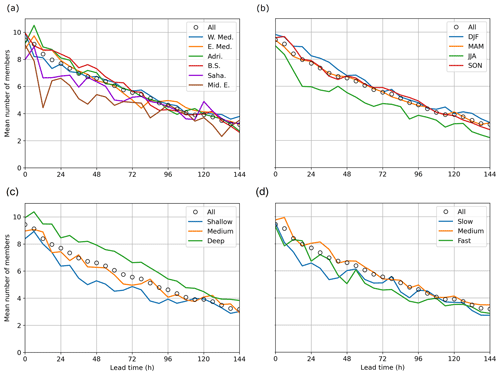
Figure 7 Difference in the mean number of ensemble members in which a cyclone is detected in the reforecasts (a) for the six regions defined in Fig. 1b, (b) for the seasonal categories (DJF, December–January–February; MAM, March–April–May; JJA, June–July–August; SON, September–October–November), (c) for the intensity-based categories defined in Fig. 3b, and (d) for the motion speed categories defined in Fig. 4. The mean number of members computed from the complete dataset is depicted by the black circles.

5 Predictability of different categories of Mediterranean cyclones

In the previous section, predictability was evaluated considering the complete dataset. In this section, cyclones are categorised following different features in order to determine the factors leading to systematically better or poorer predictability. In particular, differences in predictability are identified depending on the region, the season, the seasonality, the intensity, and the motion speed of the cyclones.

5.1 Differences in the mean number of members

The mean number of ensemble members in which a cyclone is detected (later denoted by number of members) is a key measure to investigate, as a high (low) number of members indicates high (low) predictability. In Fig. 7, the results are presented for different categories and are compared to the general pattern of Mediterranean cyclones (shown by the black circles).

In Fig. 7a, the number of members is presented as a function of the lead time for the different regional categories of Fig. 1b. Most of the categories follow the general pattern, except for the Sahara and the Middle East. In these two regions, the number of members quickly falls in the first 12 h lead time (particularly in the Middle East) and then decreases at a smaller rate until 144 h. An apparent diurnal cycle is visible, with a lower number of members every 24 h, at around 12:00 UTC, corresponding to the warmest part of the day in these regions. The season in which the cyclone occurs also has an impact on the number of members. Particularly in summer (green curve in Fig. 7b), the number of members decreases quickly in the first 18 h and then at a smaller rate until the maximum lead time. This is not the case for the other seasons, during which the decrease in the number of members follows the general pattern. Differences are also visible for different categories of intensity in Fig. 7c. The number of members detecting a cyclone is greater for deep cyclones, is lower for shallow ones, and follows the general pattern for medium-intensity cyclones. Finally, in Fig. 7d, the number of members is presented for three motion speed categories. Although differences are small, the slow and fast categories almost always lie below the general pattern of the complete dataset, which is more closely followed by the medium-speed category.

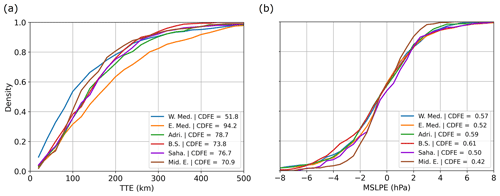
Figure 8 CDFs of the errors (a) in location and (b) in intensity at a 72 h lead time for the six regions defined in Fig. 1b.

Overall, the number of members decreases relatively strongly in the first 12 h for Saharan and Middle East cyclones (in warm regions) and in the first 18 h lead time for summer cyclones. The number of members in which a cyclone is detected is also lower for the shallowest cyclones between an 18 and 108 h lead time. Therefore, the predictability in terms of the number of members seems to be linked with the intensity of the cyclones, which are often shallow during summer. Deep winter cyclones are for their part better predicted using this metric.

5.2 From CDFs of errors to CDFE scores

For each cyclone categorisation, CDFs of errors in both location (TTE) and intensity (MSLPE) are used to compute the CDFE metric presented in Sect. 2 at a specific lead time. It should be noted that the CDFE has the same unit as the variable considered. The greater (smaller) the CDFE, the poorer (better) the predictability of the cyclone category.

To illustrate the approach, Fig. 8 presents CDFs of errors for the six regional categories presented in Sect. 3. In this representation, a category of cyclones is better predicted than another when the shape of its CDF of errors better resembles the Heaviside step function. At a 72 h lead time and for TTE (Fig. 8a), the East Mediterranean is the region in which cyclones are the least accurately predicted (orange curve), while the West Mediterranean cyclones have the smallest errors (blue curve). This is highlighted by the CDFE metric, with scores ranging from 51.8 km for the West Mediterranean to 94.2 km for the East Mediterranean. In terms of MSLPE (Fig. 8b), Middle East cyclones are the best predicted, with a CDFE of 0.42 hPa, while the Black Sea is the region in which the intensity of cyclones is the least accurately predicted at this particular lead time, with a CDFE equal to 0.61 hPa. In the next subsections, CDFE scores are computed at each lead time in order to compare the predictability between several categories of cyclones along the complete forecast duration considered.

5.3 Differences between regional categories

As shown in Fig. 1b, the spatial distribution of Mediterranean cyclones is not homogeneous, and six regions have been defined according to their cyclone density. Figure 9a presents the differences in predictability of the cyclone location, using the CDFE metric applied at each lead time to the TTEs distributions of the six regions (colour curves). It immediately appears that the location of cyclones is the best predicted in the West Mediterranean at lead times beyond 42 h. The statistical significance of the difference between this region and any other is verified between 42 and 120 h, except with the Middle East at a 78–90 h lead time. The most poorly predicted categories, namely the Adriatic and East Mediterranean cyclones, are in fact following the mean behaviour of the complete dataset (black circles) in the first 78 h. The difference between the best and the worst category is also noticeable and reaches more than 50 km at 144 h.

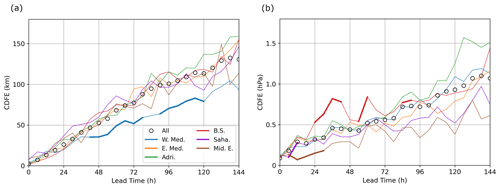
Figure 9 Differences in predictability between the regions defined in Fig. 1b, (a) for the total track error (TTE) and (b) for the MSLP error (MSLPE). The statistical significance is tested between each pair of categories, and results appear in thick lines when the considered category is significantly different from every other. CDFE scores computed from the complete dataset are represented by black circles.

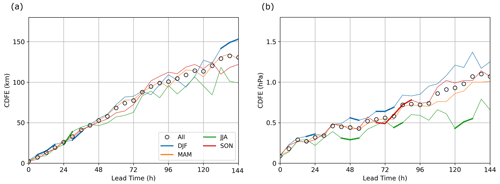
Figure 10 Differences in predictability between the seasons (e.g. DJF stands for December–January–February), (a) for the total track error (TTE) and (b) for the MSLP error (MSLPE). The statistical significance is tested between each pair of categories, and results appear in thick lines when the considered category is significantly different from every other. CDFE scores computed from the complete dataset are represented by black circles.

In Fig. 9b, the differences in predictability considering the MSLPE are presented for the complete set of six regions. Regional differences are observed, in particular between the best and the most poorly predicted categories. The Middle East is the region in which the intensity of cyclones is the best predicted at each lead time, probably linked with the absence of deep cyclones in this region (see Fig. 3a). A clear diurnal cycle is also observed, with local CDFE maxima at a 66, 90, 108, and 132 h lead time, corresponding to local times of 15:00 to 21:00 LT. While the coarse temporal resolution of 6 h does not allow for a precise timing of this behaviour, it seems that cyclones in this region experience greater errors during the warm part of the day. The cyclones in the Black Sea are the most poorly predicted in the first 72 h, and a diurnal cycle is observed with two pronounced maxima at 36 and 60 h, corresponding to the afternoon in this region. Trigo et al. (2002) already identified diurnal cycles in summer cyclones developing over northern Africa, the Iberian Peninsula, the Black Sea, and the Middle East. The maximum intensity was reached during the afternoon, while cyclolysis generally occurred in the early morning. The reason for the diurnal cycle of errors shown here could be linked with the representation of the convective processes, often occurring during the afternoons of summer days.

5.4 Differences between seasonal categories

Another possible categorisation of Mediterranean cyclones is based on the seasonality. As previously visualised, Fig. 10a presents the CDFE score for TTE and Fig. 10b presents it for MSLPE. In terms of location, winter cyclones (December–January–February) are generally less well predicted than summer ones (June–July–August), except at 24–42 h. The results are statistically significant for these two extreme seasons in the first 84 h (not shown), but differences remain under 25 km before a 120 h lead time. As a result, the season in which the cyclone occurs does not appear to be determinant in the predictability of its location.

Differences are more pronounced for the intensity, and they are statistically significant between winter and summer cyclones from 42 h until the maximum lead time (not shown). CDFE scores in the autumn and spring follow the general pattern of all Mediterranean cyclones (black circles), while errors are greater than average in winter and smaller than average in summer.

5.5 Differences between intensity categories

Differences in predictability for different intensity-based categories are shown in Fig. 11. Considering the location, the predictability is the poorest for deep cyclones between 66 h and beyond (green curve in Fig. 11a). Meanwhile, location errors are independent of the deepening rate (Fig. 11c).

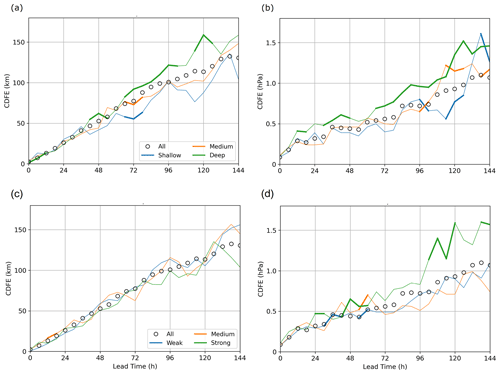
Figure 11 (a, b) Differences in predictability between three intensity-based categories of Mediterranean cyclones following their minimum MSLP, namely the 10 % shallowest cyclones, the 10 % of cyclones around the median intensity, and the 10 % deepest cyclones. (c, d) Same as (a) and (b) but based on the deepening rate, defined as the difference between the MSLP at the time of maximum intensity and 12 h before. (a, c) Results for the total track error (TTE). (b, d) Results for the MSLP error (MSLPE). The statistical significance is tested between each pair of categories, and results appear in thick lines when the considered category is significantly different from every other. CDFE scores computed from the complete dataset are represented by black circles.

In terms of MSLPE, deep cyclones are clearly more poorly predicted than average after a 66 h lead time (green curve in Fig. 11b). It is in agreement with Pantillon et al. (2017) and Pirret et al. (2017), who both showed poor prediction of the intensity of the severe European storms they investigated. However, it should be noted that, on average, the forecast intensity of deep storms in our dataset is slightly too strong from 108 h onward (not shown), while it is slightly too weak in these two previous studies. This difference could be explained not only in the region considered but also in the samples of studied cases, as Pantillon et al. (2017) and Pirret et al. (2017) find a slight under-prediction in a dataset of 25 and 60 extreme North Atlantic storms, respectively, while 280 “less extreme” Mediterranean cyclones are represented here in the deep cyclones' category. Regarding the two other categories, shallow cyclones are not necessarily better predicted than the medium category, and the difference is not always significant. The same conclusions can be drawn from the deepening rate (Fig. 11d), where rapid-intensification cyclones strike out with intensity errors greater than in the other categories after a 66 h lead time.

To summarise, the predictability is significantly poorer in terms of MSLPE for deep cyclones, at a 66 h lead time and beyond. The same conclusions can be drawn from the deepening rate, but differences are not statistically significant. As seen in Sect. 3.3, these poorly predicted cyclones tend to form during the cold part of the year (Fig. 3b), in agreement with the poorest predictability of winter cyclones shown in Sect. 5.4. They are also mainly located in the West Mediterranean and in the Adriatic, with a direct influence of the Atlantic (see Fig. 3a).

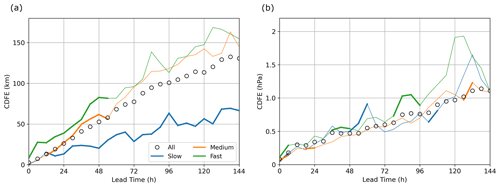
Figure 12 Differences in predictability between three motion-speed-based categories, namely the 10 % slowest cyclones, the 10 % of cyclones around the median motion speed, and the 10 % fastest cyclones, respectively, (a) for the total track error (TTE) and (b) for the MSLP error (MSLPE). The statistical significance is tested between each pair of categories, and results appear in thick lines when the considered category is significantly different from every other. CDFE scores computed from the complete dataset are represented by black circles.

5.6 Differences between motion speed categories

It has been demonstrated in Fig. 4 that different motion-speed-based categories of Mediterranean cyclones have different spatial distributions. It is consequently expected that differences will also appear in the predictability, which varies between regions (Fig. 9). Figure 12a presents the CDFE metric for a motion-speed-based categorisation of cyclones.

The link between the motion speed of the cyclone and the predictability of its location is remarkable, and differences are statistically significant from a 12–54 h lead time: the faster the cyclone, the poorer the predictability. The slow cyclones (blue curve) are clearly better predicted than any others beyond a 12 h lead time. The difference with the two other categories is statistically significant and increases as the lead time increases, reaching almost 100 km after 120 h of forecast. The particularly good predictability of these slow cyclones has to be linked with the spatial distribution highlighted in Fig. 4c. Indeed, these quasi-stationary lows are heavily concentrated in the Gulf of Genoa in the West Mediterranean, which is where the cyclone location is the best predicted (see Fig. 9). This result, considering the location, has to be compared with the predictability of the intensity of the West Mediterranean cyclones, which is not particularly well predicted. It suggests the existence of at least two different types of cyclones in this particular region. The first is made of slow cyclones (Fig. 4c), with good predictability in terms of location and fair predictability in terms of intensity. The second is constituted of fast cyclones (Fig. 4a), with poor predictability in terms of intensity and fair predictability in terms of location.

Unlike for the location, the motion speed of the cyclones does not play an important role in the predictability of the intensity (Fig. 12b) in the first 78 h. For longer lead times, the fastest cyclones are the worst predicted, but the difference with the other categories is not statistically significant beyond 96 h and does not allow for building any robust conclusions.

6 Summary and conclusions

The predictability of extratropical cyclones can be highly variable from one case to another. Here, an approach based on the use of both reanalysis and ensemble reforecasts with a fixed model configuration over 20 years makes it possible to investigate the predictability of Mediterranean cyclones in a systematic framework.

Cyclones are first tracked in the ERA5 reanalysis, providing a large reference dataset of 1960 cyclones over the 2001–2021 period. Their spatial distribution is in agreement with most of the previous climatological studies, confirming the inhomogeneity in the distribution of Mediterranean cyclones. Six preferred regions accounting for 63 % of the dataset are identified, with the Gulf of Genoa being the main hotspot in the region. In comparison to previous studies, a higher density of cyclones is found in the Adriatic. A clear seasonal cycle is highlighted, with a higher level of occurrence during the cold part of the year. The cold season is also more favourable to the development of intense cyclones, which mainly occur in the West Mediterranean, in the Adriatic, and in the north-western parts of the Black Sea.

Reference cyclones are then tracked in the homogeneous set of ensemble reforecasts for the same period. The predictability is evaluated in terms of errors in both cyclone location and intensity. Comparable magnitudes between mean error and spread indicate reasonably good reliability of the IFS ensemble reforecasts for Mediterranean cyclones. A slight over-dispersion of the ensemble can however be observed at every lead time, whether in location or in intensity. It should also be noted that while the ensemble spread is slightly greater than the mean error in most forecasts, some cyclones remain very poorly predicted with median and mean errors that can be more than 4 times greater than the ensemble spread.

Considering the entire set of cyclones, it is shown that the median location error seems to grow at two different rates with an increasing lead time. In the first about 3 d, the error grows at a nearly constant rate of 40 km d⁻¹, comparable to the one found in Picornell et al. (2011) for Mediterranean cyclones. The growth rate is however 2 times smaller for longer lead times. This behaviour is attributed to the progressive saturation of errors with lead times and to the limitation inherent to the verification of tracks against the reference. In terms of intensity error, the bias quickly reaches −0.5 hPa at a 12 h lead time, and forecasts continue to deviate at a slow rate of −0.1 hPa d⁻¹ until the maximum lead time. This indicates a slight overestimation of the intensity of forecast cyclones, in agreement with Froude et al. (2007b) for North Atlantic cyclones. This result should be regarded with some caution, as reforecasts are not compared with observational data but with reanalysis data, which may underestimate the actual cyclone intensity.

Looking at different categories of Mediterranean cyclones allows for determining several factors contributing to better or poorer predictability. It is shown that the mean number of members in which the cyclone is detected is dependent on the cyclone intensity. In particular, deep winter cyclones are detected in more members than shallower summer cyclones. In a further step, the errors are summarised for the large number of cyclone forecasts by introducing a newly defined CDFE score, which is the CRPS applied to the error distributions of location (TTEs) and intensity (MSLPEs).

In terms of cyclone location, the motion speed appears to be a key factor. In particular, the slowest Mediterranean cyclones, which are mainly located in the Gulf of Genoa, are much better predicted than any other category, at every lead time. The impact of such quasi-stationary cyclones can be considerable, as they can cause large amounts of accumulated precipitation in the same area. The predictive skill in their location is therefore important. For their part, the location of the fastest cyclones is relatively poorly predicted in the first 54 h lead time. To the authors' best knowledge, it is the first time that a link between the cyclone motion speed and predictability is highlighted. The intensity of the cyclone also plays a role, and the location of deep cyclones is less accurately predicted than in shallower categories, for lead times greater than 66 h.

Two factors leading to differences in predictability of the cyclone intensity are clearly established. First, errors in the intensity of deep cyclones are significantly greater than in any other category between a 66 h and 108 h lead time. It is in agreement with Froude et al. (2007a), who have shown a relatively poorer predictability for intense cyclones in the extratropical Northern Hemisphere. This result is also observed here for the deepening rate, where the prediction of rapid-intensification cyclones is the poorest; however, this result is not always statistically robust. A second important factor in the prediction of the intensity is the season in which the cyclone occurs. Winter cyclones are indeed less accurately predicted than summer ones. The difference between these two seasonal categories increases with the lead time and is significant from a 42 until 144 h lead time. In fact, the two factors are strongly related, as the deepest Mediterranean cyclones occur almost exclusively during the cold part of the year. The forecast skill for the intensity of those strong winter cyclones is important, as some of them account for the most destructive windstorms in the Mediterranean (e.g. Cyclone Klaus; Liberato et al., 2011). Froude et al. (2007a, b) suggested that errors in the intensity of deep cyclones could originate from an incorrect representation of their vertical structure, as the vertical tilt is known to play a major role in storm development. This hypothesis has to be verified systematically for the Mediterranean.

In this study, the predictability has been quantified in a systematic framework for several categories of Mediterranean cyclones. The motion speed of the cyclone, its intensity, the season, and the region in which it occurs all play a role. Further investigations could focus on the physical processes responsible for the loss of predictability. In particular, the quantitative importance of baroclinic and diabatic processes in the poor predictability of deep Mediterranean cyclones should be addressed. Indeed, both the representation of latent heat release in the first forecast hours and the location of Rossby wave breaking at high lead times (several days) may be responsible for part of the loss of predictability of Mediterranean cyclones. It could also be interesting to find a physical explanation to the remarkable good predictability of the shallow cyclones in the West Mediterranean.