The impact of the rotation rate on an aquaplanet's radiant energy budget: insights from experiments varying the Coriolis parameter

We investigate the effect of changes in the Coriolis force caused by changes in the rotation rate on the top-of-atmosphere (TOA) radiant energy budget of an aquaplanet general circulation model with prescribed sea surface temperatures. We analyse the effective radiative forcing caused by changes from Earth-like rotation to values between $\mathrm{1}/\mathrm{32}$ and 8 times the Earth's rotation rate. The forcing differs by about 60 W m⁻² between the fastest and slowest rotation cases, with a monotonically increasing positive forcing for faster-than-Earth-like rotations and a non-monotonically increasing negative forcing for slower rotations. The largest contributions to the forcing are due to changes in, in this order, the shortwave cloud radiative effect (SWCRE) and the clear-sky outgoing longwave radiation (OLR). From the fastest to the slowest rotation, the Hadley cell expands and the troposphere becomes drier, increasing the OLR. This contributes to negative forcing at slower-than-Earth-like rotations and to positive forcing at faster-than-Earth-like rotations. The SWCRE is influenced by changes in the low-level cloudiness within the Hadley cell and the baroclinic regime. With the expansion of the Hadley cell, the area of enhanced tropospheric stability increases, resulting in more low-level clouds, a higher SWCRE, and increased negative forcing. The non-monotonicity results from an intermediate decrease in the SWCRE caused by the disappearance of baroclinic eddies as the Hadley cell reaches global extension. At rotations faster than Earth-like, the decrease in the SWCRE, mainly due to the weakening of baroclinic eddies and storm systems, leads to an increase in positive forcing. In summary, changes in the SWCRE, driven by different circulation responses at slower-than-Earth-like and faster-than-Earth-like rotations, strongly influence the TOA radiant energy budget. These effects, along with a substantial contribution from the clear-sky OLR, could impact the habitability of Earth-like rotating planets.

1 Introduction

A slowly rotating, tidally locked planet, otherwise similar to Earth, would be much colder than its counterpart with an Earth-like rotation. This is due to the long day length associated with such slow rotation which increases the day–night temperature contrast and results in a day–night atmospheric circulation (e.g. Yang et al., 2014; Salameh et al., 2018). Such a circulation, characterized by strong ascent and thick clouds on the dayside, increases the planetary albedo and, hence, cools the planet. This effect extends the habitable zone of tidally locked planets closer to the star compared to their Earth-like counterparts (e.g. Yang et al., 2014, 2023). For faster-rotating planets, the dominant circulation shifts from day–night to equator–pole at a rotation period of about 32 Earth days, as has been shown for an Earth-like aquaplanet by Salameh et al. (2018). For planets rotating even faster, the rotation rate affects the atmospheric circulation through the Coriolis force. Variations in the Coriolis force modify the features of atmospheric circulation and can affect its radiative properties (e.g. Liu et al., 2017). However, there has not yet been a comprehensive evaluation of these effects on a planet's global radiation budget and hence its habitability.

Changes in atmospheric radiative properties have been found to affect top-of-atmosphere (TOA) radiant energy fluxes, particularly for slowly rotating to tidally locked planets. Williams et al. (2024) analyse the TOA energy flux at 23° N to discuss cloud seasonality, and Haqq-Misra et al. (2018) discuss thermal emission at the equator. Both studies highlight the importance of high clouds for TOA radiant energy fluxes in comparison to clear-sky fluxes but only at single tropical latitudes for slower-than-Earth-like rotation cases. Also for slowly rotating planets, Guzewich et al. (2020) and Way et al. (2018) analyse global averages of cloud radiative effects and water vapour but emphasize the importance of water vapour changes for the surface temperature response to rotation rate changes. Thus, both clear-sky and cloud radiative effects, which are mainly associated with changing atmospheric circulation, have been found to be important in previous studies.

Changes in the rotation rate affect the atmospheric circulation, in particular the Hadley cell and the baroclinic eddies (Hunt, 1979; Williams and Holloway, 1982; Del Genio and Suozzo, 1987; Williams, 1988; Navarra and Boccaletti, 2002), through changes in the Coriolis parameter. Based on the conservation of angular momentum, the inviscid axisymmetric theory of Held and Hou (1980) and the baroclinic instability criteria of Phillips (1954) can be used to estimate the extent and strength of the Hadley cell (e.g. Walker and Schneider, 2006). According to these theories, the Hadley cell would expand and become stronger at rotations slower than Earth-like due to the reduced Coriolis parameter. The geometry and the intensity of baroclinic eddies also depend on the rotation rate through the Coriolis parameter. These effects are quantified by eddy metrics such as the Rhines scale (e.g. Barry et al., 2002) or the Rossby radius of deformation (Eady, 1949). The former scales inversely to the square root of the meridional gradient of the Coriolis parameter, and the latter scales inversely to the Coriolis parameter itself. Previous studies using general circulation models (GCMs) have also shown that the eddy length scale is inversely related to the rotation rate (e.g. Schneider and Walker, 2006; Liu et al., 2017).

Both the changes in the Hadley cell and the baroclinic eddies caused by changes in the Coriolis parameter affect the poleward transport of momentum and heat (Cox et al., 2021; Liu et al., 2017; Navarra and Boccaletti, 2002). At the Earth's current rotation rate, the Hadley cell dominates the atmospheric momentum and heat transport at low latitudes and the eddies at mid-latitudes. With the expansion and strengthening of the Hadley cell for rotation rates slower than Earth-like, its dominance for the heat transport expands, too. For rotations faster than Earth-like, the role of the eddies becomes critical due to the shrinking of the Hadley cell. In general, the studies mentioned above have shown that the poleward atmospheric heat transport decreases with an increasing rotation rate. Liu et al. (2017), in particular, discuss the changes in the spatial pattern of clouds associated with changes in the Hadley cell that can affect the poleward heat transport. However, the consequences of such changes in the Hadley cell for the global-mean TOA radiant energy budget have not yet been discussed. The changes in the eddies can affect the cloudiness in the storm track region, which can also affect the TOA radiant energy budget. It is, however, not known if these changes are critical for the global-mean radiant energy budget.

Another consequence of the changing atmospheric circulation is the changing distribution of humidity. The ascending branch of the Hadley cell is characterized by high values of relative humidity and the descending branch by low values. Using a box model of the Hadley cell, Pierrehumbert (1995) shows that the low values of relative humidity in the descending branch are critical for maintaining tropical temperatures through the clear-sky radiative fluxes. The changes in the Hadley cell dynamics caused by the changes in the Coriolis force can be expected to affect the humidity distribution and consequently the clear-sky outgoing longwave radiation. As mentioned before, such effects have been shown to affect the surface temperature at slow rotation rates (e.g. Way et al., 2018; Guzewich et al., 2020), but their effect on the global-mean radiant energy budget has not been discussed before.

Therefore, in this paper we investigate how changes in the Hadley cell and the baroclinic eddies caused by changes in the Coriolis force affect the atmospheric properties such as temperature, humidity, and cloudiness and what consequences this has for a planet's TOA radiant energy budget. As mentioned above, previous studies have discussed some aspects of the influence of the rotation rate on the TOA radiative fluxes, with an emphasis on cloud effects (e.g. Williams et al., 2024; Liu et al., 2017; Haqq-Misra et al., 2018). However, a comprehensive evaluation of this influence on a planet's energy budget, disentangling the effects of both clear sky and clouds, as well as the shortwave and longwave parts, is still missing. This is even more the case for faster-than-Earth-like rotation rates. For this reason, unlike previous studies, we focus mainly on the rotation periods <32 Earth days and evaluate both the clear-sky and the cloud contributions to the total TOA radiant energy budget. As stated above, such an evaluation would provide further insight into the habitability of such faster-rotating planets. We therefore perform sensitivity experiments using an aquaplanet GCM with fixed sea surface temperatures (SSTs) for different Coriolis parameters representing rotation rates from $\mathrm{1}/\mathrm{32}$ to 8 times the Earth's current rotation rate, and we analyse the effective TOA radiative forcing relative to Earth-like rotation. We explain the resulting forcings in terms of changes in the atmospheric properties mentioned above and their clear-sky and cloud contributions, as well as shortwave and longwave components.

Section 2 contains a description of the model and the experimental setup. In Sect. 3, we present the changes in the atmospheric circulation, the Hadley cell, and the baroclinic eddies in comparison to previous studies. In Sect. 4 we discuss the changes in the TOA radiant energy budget and clear-sky and cloud radiative contributions due to the changes in relative humidity and cloud distribution. We summarize our results and conclude with their potential implications for planetary habitability in Sect. 5.

2 Methodology

2.1 Model description

We use the atmospheric GCM ECHAM6 (Stevens et al., 2013) in an aquaplanet configuration with prescribed SSTs. The model is run at a resolution of T63L47, i.e. a spectral truncation at 63 wavenumbers, corresponding to a Gaussian grid of about 1.9°, and 47 vertical layers up to 0.01 hPa. The model solves the radiative transfer using the Rapid Radiative Transfer Model for GCMs (RRTMG; Iacono et al., 2008) for both longwave and shortwave fluxes. The cloud cover scheme is diagnostic and calculated as a function of relative humidity (Sundqvist et al., 1989). The cloud microphysical scheme is based on the approach of Lohmann and Roeckner (1996), which includes forecast equations for cloud water and ice. The moist cumulus convection is parameterized based on the mass flux scheme of Tiedtke (1989) with modifications introduced by Nordeng (1994) to include deep convection. The non-orographic wave drag in the atmosphere is parameterized based on the Hines Doppler-spread theory (Hines, 1997a, b).

2.2 Experimental setup

We perform nine experiments in which the planetary rotation rate is set to $\mathrm{1}/\mathrm{32},\mathrm{1}/\mathrm{16},\mathrm{1}/\mathrm{8},\mathrm{1}/\mathrm{4},\mathrm{1}/\mathrm{2},\mathrm{1},\mathrm{2},\mathrm{4}$, and 8 times the current rotation rate of Earth, which is $\mathrm{\Omega }=\mathrm{7.29212}\times {\mathrm{10}}^{-\mathrm{5}}$ rad s⁻¹. The Coriolis parameter is changed accordingly in each of the experiments. We refer to the experiment with the Earth's current rotation rate as the “Earth-like” experiment. The largest rotation rate we use is $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{8}$, because the model becomes unstable for even faster rotations. Increasing the model resolution and decreasing the integration time step may help to handle such instabilities. Nevertheless, we limit our analysis to $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{8}$, which is sufficient to highlight the importance of the eddies for the radiant energy budget. There is no seasonal cycle, no continents, no topography, and no sea ice. There is a diurnal cycle, but the length of the day is the same as in the Earth-like experiment. While some of the previous studies mention that the length of the day was changed along with the rotation rate (Hunt, 1979; Del Genio and Suozzo, 1987; Williams and Holloway, 1982; Navarra and Boccaletti, 2002), other studies do not explicitly state whether a change in the rotation rate also included changes in the length of the day (Walker and Schneider, 2006; Kaspi and Showman, 2015; Liu et al., 2017). Our model setup allows us to estimate the pure effect of the changes in the Coriolis parameter via the rotation rate on the circulation and the TOA radiant energy budget. Nevertheless, this model setup can also be a useful approximation of the full effect of a realistic rotation rate change for the rates considered here. This is because for an Earth-like planet, the radiative timescale of the lower atmosphere is about 32 d (Wells, 2011). For $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}>\mathrm{1}/\mathrm{32}$, the day length is still smaller than the radiative timescale, and so the diurnal modulation is not strong enough to determine the global circulation. Williams (1988) and Salameh et al. (2018) discussed the change in the atmospheric circulation from equator–pole to day–night for $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}<\mathrm{1}/\mathrm{32}$. Salameh et al. (2018), in particular, used the same model we use to investigate the sea-ice albedo effect for changes in the Coriolis parameter and day length together. For our analysis, we consider rotation rates from $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{1}/\mathrm{32}$ to $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{8}$, where the Coriolis force dominates the circulation.

We prescribe the SSTs as a meridional profile T_s(φ) according to the Qobs distribution (Neale and Hoskins, 2000), given as

$$\begin{array}{}\text{(1)}& \begin{array}{rl}& T_{\mathrm{s}}\left(\mathit{\phi }\right)\\ & =\left\{\begin{array}{ll}\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}-{\sin }^{\mathrm{4}}\left(\frac{\mathrm{3}}{\mathrm{2}}\mathit{\phi }\right)-{\sin }^{\mathrm{2}}\left(\frac{\mathrm{3}}{\mathrm{2}}\mathit{\phi }\right)\right)\mathit{\delta }T,& \text{if}\left|\mathit{\phi }\right|\le \frac{\mathit{\pi }}{\mathrm{3}}\\ \mathrm{0},& \text{otherwise}\end{array}\right.,\end{array}\end{array}$$

where φ is latitude and δT=27 °C. This meridional SST profile is a simple geometric function close to the Earth's observed zonal-mean SST distributions and has been widely used for aquaplanet configurations of model intercomparison projects (e.g. CFMIP; Webb et al., 2017). The SST profile has a maximum of 27 °C at the equator and 0 °C at 60° N/S. As this SST distribution is hemispherically symmetric, so is the resulting climate of the aquaplanet. The results that we present are averaged over both hemispheres in the case of global means and over the northern-hemisphere meridians in the case of zonal means. Fixing the SSTs enables the analysis of the effective radiative forcing, which is the change in the net radiative flux at the TOA after adjustments of atmospheric temperatures, humidity, and clouds to the change in the rotation rate (Myhre et al., 2013). The effective radiative forcing is considered to be a good predictor of the climate resulting from a given forcing (Hansen et al., 2005; Shine et al., 2003). However, this setup does not allow us to estimate the full planetary response, which would include the adjustment of the SSTs and the feedback resulting from this. Nevertheless, our analysis shows that the circulation response, i.e. the changes in the Hadley cell and eddies to changes in the rotation rate, is similar to other studies with an interactive ocean (Liu et al., 2017; Cox et al., 2021; Navarra and Boccaletti, 2002; Kaspi and Showman, 2015). This shows that much of the signal is a direct response to the changes in the rotation rate rather than a feedback. We ran all the experiments for 40 years. The results presented below are time averages over the last 30 years of each experiment, ignoring the first 10 years of spin-up; 30 years of simulations is a large sample, so the differences in the atmospheric quantities between different rotation rates are highly significant, and the error bars are not visible in the global mean. The quantities representing baroclinic activity are calculated using 1 h instantaneous data over a month. In this case, the northern and southern hemispheres have been combined to double the sample size.

3 Atmospheric circulation

In this section, we describe the changes in the atmospheric circulation caused by changes in the rotation rate and compare them to results from previous studies.

3.1 Effects of the rotation rate on the meridional circulation

3.1.1 Hadley cell

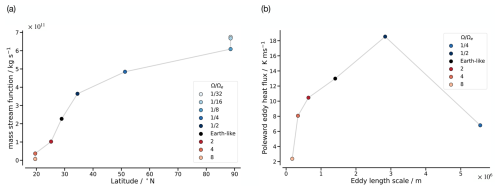
Based on the Hadley cell theory (Held and Hou, 1980) and results from previous GCM studies, we expect the Hadley cell to expand at slower-than-Earth-like rotation rates. We define the extent of the Hadley cell as the latitude at which the mass stream function changes sign when averaged between 400 and 700 hPa. This definition is similar to that of Del Genio and Suozzo (1987), who, however, used only the 500 hPa pressure level without averaging over an altitude range. Figure 1 shows the overturning meridional mass stream function for different rotation rates. For Earth-like rotation, the Hadley cell extends from the equator to about 30° N/S, similar to the Earth's Hadley cell under equinoctial conditions. At rotations slower than Earth-like, for $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{1}/\mathrm{2}$ and $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{1}/\mathrm{4}$, the Hadley cell expands and moves the mid-latitude jets poleward. At $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{1}/\mathrm{8}$, the Hadley cell expands almost to the poles. The mid-latitude jets and the associated eddies move poleward and become stronger from $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{1}/\mathrm{2}$ to $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{1}/\mathrm{8}$ (not shown), similar to in previous studies (Navarra and Boccaletti, 2002). For further reduction in rotation rates, $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{1}/\mathrm{16}$ and $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{1}/\mathrm{32}$, a single overturning Hadley cell covers both hemispheres. These results are qualitatively consistent with previous studies, regardless of the GCM setup used (Del Genio and Suozzo, 1987; Navarra and Boccaletti, 2002). Small differences between studies could be due to the use of different metrics to determine the extent of the Hadley cell or to different model setups. For slower ($\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}<\mathrm{1}/\mathrm{2}$) and faster ($\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{8}$) rotations, the latitudinal extent of the Hadley cell differs in the upper and lower troposphere, motivating the use of the mean mass stream function between 400 and 700 hPa as a metric.

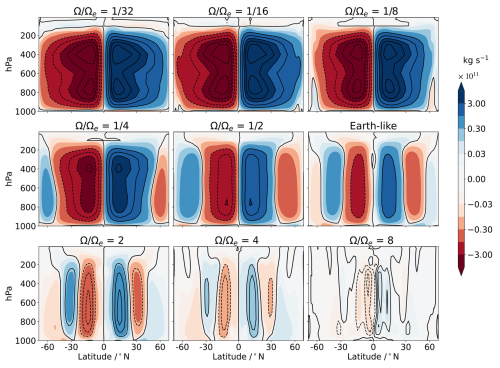
Figure 1 Mass stream function of the zonal-mean meridional circulation for different rotation rates. Positive values refer to clockwise and negative values to anti-clockwise circulation. The shaded intervals follow an exponential scaling. From $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{1}/\mathrm{32}$ to Earth-like, the contour interval is $\mathrm{1}\times {\mathrm{10}}^{\mathrm{11}}\mathrm{kg}{\mathrm{s}}^{-\mathrm{1}}$, and for $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{2}$, 4, and 8, the contour intervals are changed to 0.25×10¹¹, 0.1×10¹¹, and $\mathrm{0.02}\times {\mathrm{10}}^{\mathrm{11}}\mathrm{kg}{\mathrm{s}}^{-\mathrm{1}}$, respectively.

Similarly to the extent, the strength of the Hadley cell increases as the rotation rate decreases according to Held and Hou (1980) and as shown by Walker and Schneider (2006). Here we define the strength of the Hadley cell as the maximum absolute value of the mass stream function (Liu et al., 2017; Walker and Schneider, 2006). Figure 2a shows the dependence of the strength and extent of the Hadley cell on the rotation rate. The strength increases with the extent from $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{4}$ to $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{1}/\mathrm{8}$. For $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}\le \mathrm{1}/\mathrm{8}$, the Hadley cell is global and can no longer expand. However, it still becomes stronger, albeit slightly. Even a small increase in the strength of the Hadley cell for $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}\le \mathrm{1}/\mathrm{8}$ seems to have a large effect on the thermal and radiative properties. Figure 2a also shows that the faster rotations, $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{4}$ and $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{8}$, seem to have similar extents in the averaged stream function between 400 and 700 hPa. To our understanding, theory does not provide an explanation for the Hadley cell approaching a minimum extension near $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{4}$. However, the Hadley cell becomes weaker at $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{8}$ than at $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{4}$. In the following sections we will show that the limit of the Hadley cell expansion at $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{1}/\mathrm{8}$ has consequences for the radiant energy budget. On the other hand, the apparent limit for fast rotation at about $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{8}$ does not.

Figure 2 (a) Latitudinal extent vs. strength of the Hadley cell, based on the mass stream function at different rotation rates. (b) Eddy length scale vs. Eddy heat flux at different rotation rates.

3.1.2 Baroclinic eddies and the Ferrel cell

Baroclinic eddies are known to induce a mid-latitude Ferrel cell in the zonal-mean atmospheric circulation, and the eddy fluxes affect the strength of the Ferrel cell (e.g. Chang, 1996). Therefore, we consider the changes in the eddies to affect the zonal-mean Ferrel cell, similarly to Navarra and Boccaletti (2002). According to the Eady theory of baroclinic instability, the baroclinic eddy length scale L is proportional to the Rossby radius of deformation (Eady, 1949), i.e. the length scale at which rotational effects become important. L is given as $c_d\frac{NH}{f}$ with empirical constant c_d chosen to be 1.35 (Schneider and Walker, 2006); N is the static stability, H is the scale height, and f is the Coriolis parameter. This suggests that for increasingly faster rotations, the baroclinic eddy length scale decreases, which has been confirmed by GCM studies (e.g. Schneider and Walker, 2006; Kaspi and Showman, 2015; Liu et al., 2017). Figure 2b shows the changes in the eddy length scale L and eddy heat flux $\stackrel{\mathrm{‾}}{v^{\prime }{\mathit{\theta }}^{\prime }}$ in our simulations. $\stackrel{\mathrm{‾}}{v^{\prime }{\mathit{\theta }}^{\prime }}$ is the poleward eddy heat flux, where v is the meridional wind and θ is the potential temperature. The bar and prime denote the mean and deviation in time, respectively. Both L and $\stackrel{\mathrm{‾}}{v^{\prime }{\mathit{\theta }}^{\prime }}$ are calculated within the baroclinic zone, with the boundaries defined as the outermost latitudes where the $\stackrel{\mathrm{‾}}{v^{\prime }{\mathit{\theta }}^{\prime }}$ at 500 hPa exceeds 30 % of its maximum value. The outermost edges of the baroclinic zone are marked in Fig. 3a for $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}\ge \mathrm{1}/\mathrm{4}$. These limits are calculated following Wang et al. (2018) except that we use 500 hPa instead of 800 hPa. The results are, however, consistent at lower-tropospheric pressure levels. The activity of the eddies decreases for increasingly faster rotations than Earth-like, as both L and $\stackrel{\mathrm{‾}}{v^{\prime }{\mathit{\theta }}^{\prime }}$ decrease. The eddy momentum flux $\stackrel{\mathrm{‾}}{v^{\prime }{u}^{\prime }}$ (see Fig. S1 in the Supplement) shows a similar dependence on the rotation rate.

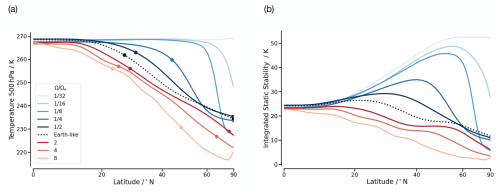
Figure 3 Zonal-mean (a) temperature at 500 hPa and (b) integrated static stability from 1000 to 400 hPa for different rotation rates. The dots in panel (a) mark the outermost edges of the baroclinic zone.

In the zonal mean, the meridional mass stream function (Fig. 1) shows the presence of the Ferrel cell poleward of the Hadley cell at mid-latitudes for the Earth-like scenario. For faster-than-Earth-like rotations, the Ferrel cell weakens and shrinks due to the reduction in $\stackrel{\mathrm{‾}}{v^{\prime }{\mathit{\theta }}^{\prime }}$ and L. For slower rotations, L increases as mentioned above. $\stackrel{\mathrm{‾}}{v^{\prime }{\mathit{\theta }}^{\prime }}$ reaches a maximum at $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{1}/\mathrm{2}$ and reduces after that. For such slow rotations, the eddies are shifted poleward, where their activity is constrained by the size of the planet. At $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{1}/\mathrm{8}$, when the Hadley cell reaches the poles, baroclinic eddies do not occur, which leads to the disappearance of the Ferrel cell. Similar results have been discussed by Del Genio and Suozzo (1987) and Navarra and Boccaletti (2002). For such slower rotations, as mentioned by Del Genio and Suozzo (1987), the Rossby radius of deformation is much larger (an order of magnitude) than the size of the planet and therefore baroclinic instability cannot occur. In the following sections, we will show that for $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}>\mathrm{1}/\mathrm{8}$, the changes in the baroclinic instability affect the storm systems, with important consequences for the radiant energy budget of the planet.

3.2 Effects of the rotation rate on the thermal structure

3.2.1 Horizontal structure

In the Earth-like scenario, the tropical free troposphere is characterized by weak temperature gradients (WTGs) (e.g. Sobel et al., 2001) due to the weak Coriolis force near the equator. Figure 3a shows the zonal-mean free-tropospheric temperature profiles at 500 hPa for different rotation rates. When the Coriolis force is weaker than Earth-like, gravity waves are efficiently smoothing out the temperature differences over a wider range of latitudes. Therefore, the free tropospheric vertical temperature profile is similar to the equatorial temperature profile over a wider range of latitudes for slower rotation cases. This expansion of the WTG region shifts the strong meridional temperature gradient, and with it the baroclinic eddy activity, poleward. This is indicated by the meridional temperature profile at 500 hPa shown in Fig. 3a. The transition from the subglobal to the global Hadley cell occurs at $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{1}/\mathrm{8}$, and the meridional temperature gradient disappears completely at $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{1}/\mathrm{32}$; i.e. the baroclinic eddy activity becomes negligible at $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{1}/\mathrm{8}$ and disappears completely at $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{1}/\mathrm{32}$. In the other direction, for faster-than-Earth-like rotation, the WTG region becomes narrower. However changes in the strength of the meridional temperature gradient are small (Fig. 3a). With minimal or no change in the meridional temperature gradient, the thermal wind balance suggests that the increase in the Coriolis parameter from $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{2}$ to $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{8}$ decreases the vertical wind shear (see Fig. S4). Weaker vertical wind shear leads to weaker eddies, weaker storms, and reduced meridional energy transport. The increasing temperature difference from $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{1}/\mathrm{4}$ to $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{8}$ between the equator and the poles is a consequence of this (e.g. Schneider and Walker, 2006; Kaspi and Showman, 2015).

3.2.2 Vertical structure

Figure 3a shows warmer temperatures at 500 hPa for slower rotation cases compared to the Earth-like scenario. This is consistent with the increase in vertically integrated static stability S for slower rotation shown in Fig. 3b. The vertical integrated static stability is defined as

$$\begin{array}{}\text{(2)}& S=\underset{p_{\mathrm{b}}}{\overset{p_{\mathrm{t}}}{\int }}-T\times {\displaystyle \frac{\mathrm{d}\left[\log \right(\mathit{\theta }\left)\right]}{\mathrm{d}p}}\mathrm{d}p,\end{array}$$

where the integration is performed over the troposphere from p_b=1000 to p_t=400 hPa. T is the temperature and θ the potential temperature of the air. The boundary layer temperature is strongly constrained by the prescribed SST. Hence, the changes in stability are mainly related to the changes in free-tropospheric temperature. Due to the extension of the WTG region, the free troposphere is warmer over a wider range of latitudes at slower rotations. This effect increases the static stability for slower rotations, especially over the descending branch of the Hadley cell, which we will show in later sections has an important effect on the forcing. The larger instability for faster rotation leads to increased convective activity and increased convective precipitation at higher latitudes (see Fig. S2a).

4 Radiant energy budget at the TOA

The effective forcing at the TOA for faster and slower rotations relative to Earth-like is shown in Fig. 4. For faster rotations, there is a monotonic increase in positive forcing. For slower rotations, there is generally an increase in the negative forcing, which is, however, not monotonic. The increase in the negative forcing is interrupted by a drop to almost zero forcing at $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{1}/\mathrm{8}$. This drop is an actual signal that we have confirmed by additional experiments with rotation rates slightly larger and smaller than $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{1}/\mathrm{8}$ (see Fig. S3).

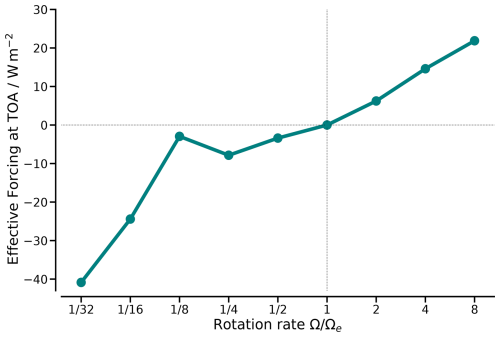
Figure 4 Effective radiative forcing at the TOA for different rotation rates with respect to an Earth-like rotation rate.

To understand the sources of the changes in the forcing, we decompose the TOA radiant energy budget into contributions from shortwave (SW) and longwave (LW) radiation under clear-sky and all-sky conditions (Fig. 5). The global-mean clear-sky net incoming SW radiation is almost constant over the rotation rates. The small differences in this quantity are due to small differences in the water vapour absorption. The global-mean clear-sky outgoing LW radiation (OLR), on the other hand, varies considerably when the rotation rate is changed. The global-mean LW cloud radiative effect (LWCRE) varies little with the rotation rate compared to its counterpart, the SW cloud radiative effect (SWCRE). The effective forcing differs by about 63 W m⁻² between the slowest and fastest rotation cases. The difference in the SW cloud radiative effect is 47 W m⁻²; i.e. it contributes almost $\mathrm{3}/\mathrm{4}$ to the effective forcing. The remaining contribution is mainly provided by the clear-sky OLR. In the following subsections, we will discuss the effect of the rotation rate on the clear-sky radiation first and then its effect on the cloudiness and the cloud radiative effects.

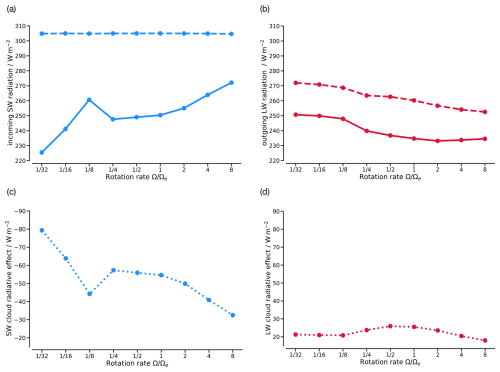
Figure 5 Global-mean TOA (a) net incoming SW clear-sky (dashed line) and all-sky (solid line) radiation, (b) outgoing LW clear-sky (dashed line) and all-sky (solid line) radiation, (c) SW cloud radiative effect, and (d) LW cloud radiative effect for different rotation rates.

4.1 Effects of the rotation rate on the clear-sky radiation

The changes in the net clear-sky radiation at the TOA are mainly due to changes in the clear-sky OLR due to the changes in the atmospheric circulation, which alter the temperature and humidity distribution.

The effective emission of LW radiation to space comes mainly from the descending branch of the Hadley cell (Pierrehumbert, 1995), which is characterized by relatively high free-tropospheric temperatures and low humidity. Therefore, as the rotation rate decreases, a substantial increase in the clear-sky OLR from the descending branch of the Hadley cell is mainly due to an increase in temperature, resulting from the extended WTG region, and a decrease in specific humidity, caused by accelerated subsidence over the extended descending branch. We analyse the effect of these changes on the clear-sky OLR through analysing changes in column relative humidity (ℛ_col). In the spectral regions where the atmospheric emission to space originates mainly from water vapour, this emission remains constant under temperature change if the relative humidity stays constant (Ingram, 2010; Jeevanjee et al., 2021; Stevens and Kluft, 2023). A reduction in relative humidity would lead to a downward shift of the effective emission height, a related increase in the emission temperature, and hence more OLR. ℛ_col is defined as the relative humidity over the tropospheric column and is given as

$$\begin{array}{}\text{(3)}& {\mathcal{R}}_{\text{col}}={\displaystyle \frac{{\int }_{p_{\mathrm{b}}}^{p_{\mathrm{t}}}q\mathrm{d}p}{{\int }_{p_{\mathrm{b}}}^{p_{\mathrm{t}}}{q}_{\mathrm{s}}\mathrm{d}p}},\end{array}$$

where ${\int }_{p_{\mathrm{b}}}^{p_{\mathrm{t}}}q\mathrm{d}p$ and ${\int }_{p_{\mathrm{b}}}^{p_{\mathrm{t}}}{q}_{\mathrm{s}}\mathrm{d}p$ are specific humidity and saturation specific humidity, both integrated over the atmospheric column from p_b=1000 hPa to p_t=100 hPa. Figure 6a shows the zonal-mean ℛ_col that nicely anticorrelates with the zonal-mean clear-sky OLR for different rotation rates. For Earth-like rotation, low ℛ_col values are simulated from about 10 to 45°. For slower rotations, the descending branch of the Hadley cell expands and its subsidence accelerates, increasing the free-tropospheric temperature and reducing the humidity. Consequently, the low ℛ_col values are further reduced and extend to higher latitudes, increasing in the clear-sky OLR for slower rotation cases up to $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{1}/\mathrm{8}$. The ℛ_col of the ascending branch remains similar to Earth-like for both faster and slower rotations, and hence the clear-sky OLR changes less at the ascending branch. For $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}<\mathrm{1}/\mathrm{8}$, when the Hadley cell is no longer expanding, the dryness of the descending branch still increases due to the continuing increase in the strength of the Hadley cell. This results in a further increase in the clear-sky OLR, even after the Hadley cell becomes global.

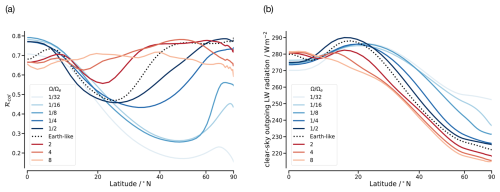
Figure 6 Zonal-mean (a) column relative humidity ℛ_col and (b) clear-sky outgoing longwave radiation for different rotation rates.

For faster rotations, the free-tropospheric temperature decreases and the humidity increases due to the shrinking effect of the Hadley cell and the deceleration of the subsidence region. However, the decrease in the global-mean clear-sky OLR with faster rotation is not only caused by changes in the Hadley cell. Temperatures at middle and high latitudes are also reduced due to inefficient heat transport by weaker and smaller baroclinic eddies. Consequently, the contribution of middle and high latitudes to the clear-sky OLR is reduced. In general, increasingly weaker circulations at faster rotations lead to higher ℛ_col across most latitudes. At $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{8}$ the zonal-mean ℛ_col is large and homogeneous from the equator to the poles.

The changes in humidity with rotation rate are consistent with previous studies using different experimental setups. Way et al. (2018) and Guzewich et al. (2020) identified the decrease in column water vapour as an important reason for the surface cooling for reduced rotation rates, in setups with both a dynamical ocean and the presence of land. However, in simulations where SSTs are allowed to adjust, the clear-sky OLR response would be determined not only by changes in atmospheric water vapour and temperature but also by SST feedbacks. This is likely why in the case of Liu et al. (2017), who analyse rotation rates similar to ours but in a slab ocean setup, the zonal-mean clear-sky OLR generally increases with the rotation rate (their Figs. 8c and 9c), except for latitudes poleward of about 50°. In our case, this is true only near the equator (Fig. 6b).

4.2 Effect of the rotation rate on the cloud distribution

Figure 7 shows the cloud distribution and the meridional mass stream function for different rotation rates. In the zonal mean, there is a gradual transition from a more uniform occurrence of low clouds to high clouds at the descending branch of the Hadley cell and at the storm tracks from slower to faster rotation. For the Earth-like scenario, the zonal-mean cloud distribution shows maxima at the ascending branch of the Hadley cell and at the storm tracks. The descending branch of the Hadley cell has the characteristic low clouds. At slower-than-Earth-like rotations, the expansion of the Hadley cell and the enhanced tropospheric stability over an extended region increase the occurrence of low clouds. Near the equator, the high cloud fraction increases at the ascending branch of the Hadley cell due to stronger convection. When the Hadley cell changes from subglobal to global at $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{1}/\mathrm{8}$, the clouds associated with the storm tracks disappear. For $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}<\mathrm{1}/\mathrm{8}$, i.e. in the case of a global Hadley cell, low clouds occur at all latitudes and increase the global-mean cloud fraction and liquid water path (Fig. 10a and b). In the other direction from $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{1}/\mathrm{4}$ to 8, as the rotation rate increases, the occurrence of high clouds increases due to an increasingly unstable atmosphere and convective activity extending from low to high latitudes. However, the impact of the increased occurrence of high clouds on the total radiant energy budget is relatively small. Rather, it is the reduction in low clouds, especially in the storm track regions, at faster rotations that is important.

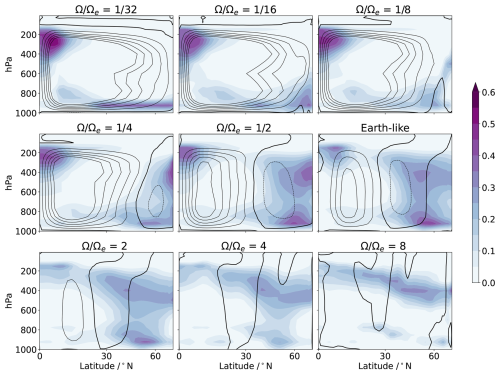
Figure 7 Zonal-mean cloud fraction (purple shading) and mass stream function (contours) over the northern hemisphere for different rotation rates. Positive stream function values are indicated by solid lines and negative stream function values by dashed lines. The contour interval is $\mathrm{0.5}\times {\mathrm{10}}^{\mathrm{11}}\mathrm{kg}{\mathrm{s}}^{-\mathrm{1}}$ for all rotation rates.

At Earth-like rotation, stronger storms tend to be more cloudy, which increases the cloud albedo (Hadas et al., 2023). The eddy length scale decreases with the rotation rate, so from $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{1}/\mathrm{4}$ to $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{8}$, the synoptic-scale storm systems in our simulations become smaller but more numerous. The alternating high- and low-pressure systems in the mid-latitudes for Earth-like rotations become much smaller and more numerous with increasing rotation rate (see Fig. S5), indicating the occurrence of smaller storm systems. There are two types of cloudiness associated with such storm systems: (a) convective and (b) stratiform. The convective mode tends to be deep and more localized, while the stratiform mode is widespread in the middle and lower levels of the troposphere (Houze, 2004). The cloudiness of the storm systems on the poleward flank of the Ferrel cell is positively correlated with the variance of the vertical velocity (Datseris et al., 2022). A comparison of Figs. 7 and 8 shows that for faster-than-Earth-like rotations, the reduction in storm track cloudiness, in particular of the low- and middle-level clouds, corresponds well to the reduction in vertical wind variance. This is because for increasingly faster rotations, the geostrophic balance leads to increasingly weaker winds due to the increasing Coriolis parameter. Together with the smaller eddy length scale, the weaker winds result in smaller and weaker synoptic-scale storm systems. Consequently, the stratiform clouds associated with storm systems are reduced at faster rotations. However, the reduction in vertical wind variance does not explain the expansion of high clouds at faster rotations. At increasingly faster rotations, the tropospheric stability decreases (Fig. 3b) and the convective precipitation increases over middle and high latitudes (see Fig. S2a). Both together suggest that the expansion of high clouds is more likely due to convective activity extending to high latitudes.

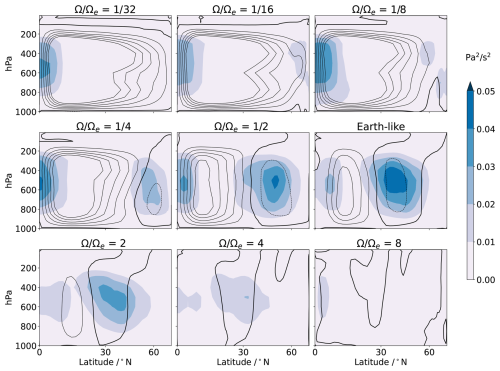
Figure 8 Zonal-mean variance of hourly instantaneous vertical velocity (blue shading) calculated from the monthly mean vertical velocity and mass stream function (contours) over the northern hemisphere for different rotation rates. Positive stream function values are indicated by solid lines and negative stream function values by dashed lines. The contour interval is $\mathrm{0.5}\times {\mathrm{10}}^{\mathrm{11}}\mathrm{kg}{\mathrm{s}}^{-\mathrm{1}}$ for all rotation rates.

4.3 Effects of the rotation rate on the all-sky radiation

As mentioned earlier, Fig. 5a and b show that the all-sky OLR increases similarly to its clear-sky part for slower rotations. The net incoming SW radiation generally decreases for slower rotations due to the increase in the SWCRE, but the behaviour is non-monotonic at $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{1}/\mathrm{8}$.

The change in the SWCRE is the dominant contribution (about $\mathrm{3}/\mathrm{4}$) to the TOA radiative forcing (Fig. 4). Figure 9a shows the zonal-mean SWCRE for different rotation rates where the changes are non-linear from middle to high latitudes. The global mean of the total and low cloud fraction from Fig. 10a and c shows that changes in the SWCRE with the rotation rate are mainly due to changes in the low clouds. For Earth, the main contribution to the SWCRE comes from the storm tracks (Hadas et al., 2023), which is also seen in our Earth-like simulation (Fig. 9a). As the rotation rate in our experiments increases, the SWCRE decreases due to the reduction in cloudiness mainly at the storm tracks and, to a lesser degree, at the Hadley cell. This can be seen from Fig. 9c and a, which show that the zonal-mean low cloud fraction and SWCRE are reduced for faster rotation mainly between 35 and 60°. Although the storm systems shift towards the equator with increasing rotation (Fig. 9c), the reduction in the low-level cloud fraction dominates the higher insolation at lower latitudes such that the SWCRE is strongly reduced with increasing rotation. For a reduction in the rotation rate from Earth-like to $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{1}/\mathrm{4}$, the increasing extent and strength of the Hadley cell favour cloudiness at the ascending and descending branches. The increase in the sharp meridional temperature gradient and the eddy length scale favour larger and stronger storms. However, the storms are also shifted poleward, where their meridional extent is limited by the size of the planet (see Sect. 3.1.2) and where they experience less insolation. This reduces the SWCRE in the storm track region for these rotations. The increase at the Hadley cell and decrease at the storm tracks are largely compensated in the global-mean SWCRE for $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{1}/\mathrm{2}$ and $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{1}/\mathrm{4}$ (Fig. 5c). At $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{1}/\mathrm{8}$, the global-mean SWCRE and the zonal-mean SWCRE drop due to the disappearance of the storm tracks. For $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}<\mathrm{1}/\mathrm{8}$, the SWCRE increases sharply. This is because for these rotations, a small increase in the strength of the Hadley cell leads to a large increase in the stability of the troposphere. The low cloud fraction and the liquid water path increase, as can be seen from Fig. 10b and c. The larger the liquid water path and hence the optical thickness, the larger the SWCRE.

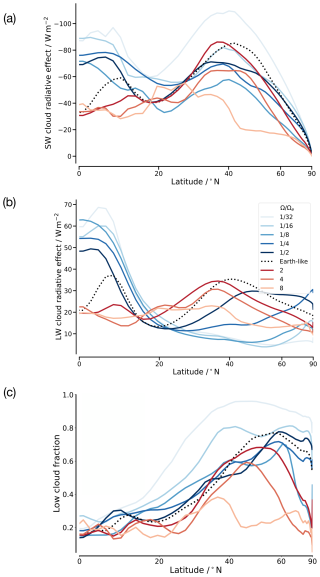
Figure 9 Zonal-mean (a) shortwave and (b) longwave cloud radiative effect and (c) low cloud fraction for different rotation rates.

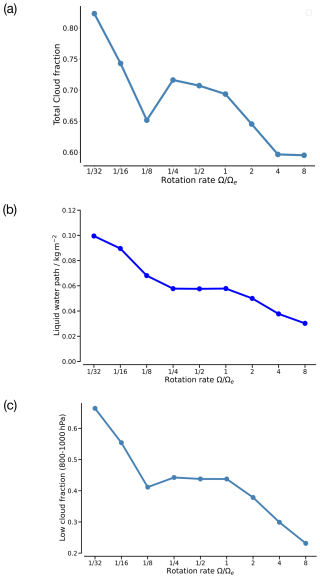
Figure 10 Global-mean (a) total cloud fraction, (b) liquid water path, and (c) total low cloud fraction for different rotation rates.

The global-mean LWCRE has a maximum near $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{1}/\mathrm{2}$ and reduces similarly for both slower and faster rotation (Fig. 5d). This non-linear change in the LWCRE is due to the extent and fraction of the high clouds acting in opposite directions for slower and faster rotations. For slower-than-Earth-like rotations, the high cloud fraction increases, but the extent decreases due to a larger subsidence region. The zonal mean LWCRE is shown in Fig. 9b. The increase in high clouds near the equator increases the LWCRE. However, the effect is small because the increase in humidity already limits the OLR. The LWCRE at the storm tracks is reduced for $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{1}/\mathrm{2}$ and $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{1}/\mathrm{4}$ because they are located very close to the poles compared to at Earth-like rotation, where the emission temperature of their clouds is low. At faster-than-Earth-like rotations, the extent of the high clouds expands spatially (Fig. 7) due to convective activities over middle and high latitudes (discussed above). However, near the equator, the high cloud fraction decreases due to the weakening of the Hadley cell. Both these effects result in a more meridionally uniform distribution of the high clouds and the LWCRE. This is similar to the distribution of R_col (discussed above), which becomes uniform for faster rotations around $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{8}$.

The changes in the zonal-mean cloud radiative effects are similar to those simulated by Liu et al. (2017) in a slab ocean setup using GFDL AM2.1. Both LW and SW cloud radiative effects decrease from slower to faster rotation near the equator, providing a robust response to Hadley cell changes with the rotation rate. The changes in storm systems and associated cloud radiative effects simulated in our experiments are not apparent in Liu et al. (2017). Williams et al. (2024), however, report a non-monotony in the SWCRE similar to that simulated by us. Their experiments are performed with a slab ocean setup of the Isca model, where $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{1}/\mathrm{8}$ is at the transition point from eddy-dominated at high rotation rates to mean-flow-dominated at slow rotation rates, and such transitional rotation rates appear to suppress cloud formation. Our reasoning for the non-monotony is similar to that of Williams et al. (2024), in that the Rossby radius of deformation reaches the size of the planet at $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{1}/\mathrm{8}$, causing the storm tracks to disappear and the SWCRE to drop. While the studies of Liu et al. (2017) and Williams et al. (2024) differ in their experimental and model setup compared to our study, these similarities in results suggest that the responses of the circulation and cloud radiative effects to changes in rotation rate are qualitatively robust across models.

5 Summary and conclusion

We investigated the effects of changes in the Coriolis force induced by changes in the rotation rate of an Earth-like aquaplanet on its temperature, humidity, and cloudiness and subsequently on its TOA radiant energy budget. We performed sensitivity experiments with an aquaplanet GCM by varying the Coriolis parameter according to rotation rates from $\mathrm{1}/\mathrm{32}$ to 8 times Earth's rotation, while keeping all other parameters, including the day length and the SST distribution, fixed. This approach enables us to analyse the effective radiative forcing caused by a change in the rotation rate. It differs by about 60 W m⁻² between the fastest and slowest rotation cases. This large difference is due to very different atmospheric circulations that create different relative humidity and cloud distributions. These factors lead to a monotonically increasing positive forcing at increasing rotation rates and a non-monotonically increasing negative forcing at decreasing rotation rates relative to Earth-like. About $\mathrm{3}/\mathrm{4}$ of the contribution to the forcing comes from the changes in the SWCRE, and the remaining part comes from the clear-sky OLR.

The clear-sky OLR changes due to changes in free-tropospheric temperature and humidity. For slower-than-Earth-like rotations, the expansion and strengthening of the Hadley cell result in an extended and much drier descending branch. The Hadley cell becomes global for $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}<\mathrm{1}/\mathrm{8}$, beyond which it can no longer expand. However, its strength, and with it the subsidence over the descending branch, increases further for even slower rotation. The expansion and the accelerated subsidence of the Hadley cell, and the latter alone in the case of $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}<\mathrm{1}/\mathrm{8}$, lead to an increasingly warmer and less humid atmosphere at slower rotations, i.e. an atmosphere with lower relative humidity and larger clear-sky OLR. For faster-than-Earth-like rotations, the tropics become more humid due to a weaker Hadley cell and the extra-tropics become colder due to weaker baroclinic eddies. Both of these effects reduce the clear-sky OLR at faster rotations. The rotational dependence of the clear-sky OLR is consistent with changes in the circulation, especially the Hadley cell, and affects the forcing as expected.

The changes in the cloud distribution, especially those in low clouds caused by variations in the Coriolis force, strongly affect the SWCRE and the TOA radiant energy budget. For $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}>\mathrm{1}$, the increasingly weaker storm systems reduce the SWCRE more than the weaker Hadley circulation does. This reduction is the dominant contribution to the positive forcing at faster rotations. From Earth-like to $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{1}/\mathrm{8}$, the expansion and acceleration of the Hadley cell increase the region of enhanced tropospheric stability and the low-level cloudiness. The expansion of the Hadley cell moves the eddies and the storm tracks poleward, where the storms are limited by the size of the planet. The SWCRE increases at the Hadley cell but decreases at the storm tracks, and these two effects are compensated in the global mean. The disappearance of the storm tracks at $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{1}/\mathrm{8}$ causes a decrease in the SWCRE and a non-monotonic behaviour in the increasing negative forcing for slower rotations. For $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}<\mathrm{1}/\mathrm{8}$, the further enhanced stability of the lower troposphere within the globally extended Hadley cell increases the low-level cloudiness and the SWCRE sharply. Our analysis concludes that changes in tropospheric stability at slower rotations and changes in baroclinicity at faster rotations are particularly important for the SWCRE. The presence of baroclinic eddies and associated storm systems influences the TOA radiant energy budget for $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}>\mathrm{1}/\mathrm{8}$. Further, the variations in the storm systems are crucial for $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}>\mathrm{1}$ due to their dominant role in the positive forcing.

We expect these responses to rotation rate changes to be qualitatively consistent across different models because the model results are supported by physical arguments. Indeed, for example, the decrease in humidity at slower rotations and the drop in the SWCRE at $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{1}/\mathrm{8}$ have been identified in simulations by Way et al. (2018) and Williams et al. (2024), respectively. However, our results are uncertain because the largest part of the forcing is due to changes in cloudiness, and cloud radiative responses to forcing are generally a large source of uncertainty in GCMs (Ceppi et al., 2017). In addition, the small-scale baroclinic eddies and storm systems simulated for the fast rotation cases may not be well represented due to our relatively coarse model resolution. It should also be emphasized that the relationship between forcings and surface temperature responses in an interactive ocean setting would probably not be linear, due to the state-dependent nature of feedback mechanisms. For instance, a more humid atmosphere generally has a reduced Planck feedback (e.g. Bourdin et al., 2021), which, for our results, implies that the same forcing at faster rotation will cause a larger temperature response. Sea ice, which is ignored in our simulations, could provide a positive feedback and affect aquaplanet simulations quite strongly (e.g. Rose et al., 2013).

While our forcing estimates are influenced by these caveats and the assumptions made in the simulations, we still find it instructive to estimate their potential influence on the habitability of a planet. Earlier studies vary considerably in their estimates of the Sun's habitable zone (e.g. Zsom et al., 2013; Gómez-Leal et al., 2019). A commonly used definition, given by Kasting et al. (1993), is that habitability requires the presence of liquid water on the planet's surface. The inner edge of the habitable zone is then determined by water loss through photolysis and hydrogen escape. Based on this definition, Kasting et al. (1993) estimated the Sun's habitable zone to be between 0.95 and 1.37 au. Assuming a global-mean TOA insolation of 340 W m⁻² and a planetary albedo of 0.3, a negative forcing of −40 W m⁻², like in our case of $\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{1}/\mathrm{32}$, would be equivalent to moving Earth to a distance from the Sun of 1.1 au. A positive forcing of 20 W m⁻² ($\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{e}}=\mathrm{8}$) would be equivalent to moving Earth to 0.93 au. Thus, we infer that the increasing positive forcing at faster-than-Earth-like rotations, caused by increasing humidity and decreasing planetary albedo, can shift the planet to the inner edge of the habitable zone, even if the incoming solar radiant energy remains unchanged. This suggests that sufficient changes in the Coriolis force alone can substantially affect the habitability of Earth-like rotating planets.